Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
MILATOVIC, OGNJEN
2005.
POSITIVE PERTURBATIONS OF SELF-ADJOINT SCHRÖDINGER OPERATORS ON RIEMANNIAN MANIFOLDS.
International Journal of Geometric Methods in Modern Physics,
Vol. 02,
Issue. 04,
p.
543.


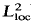 ) of an essentially self-adjoint Schrödinger operator
) of an essentially self-adjoint Schrödinger operator 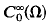 is again essentially self-adjoint if
is again essentially self-adjoint if 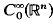 is given.
is given.