Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-02T19:06:06.036Z Has data issue: false hasContentIssue false
  • English
  • Français

Point interactions on bounded domains

Published online by Cambridge University Press:  14 November 2011

Wim Caspers  and
Guido Sweers
Wim Caspers
Affiliation:
Department of Pure Mathematics, Delft University of Technology, P.O. Box 5031, 2600 GA Delft, The Netherlands
Guido Sweers
Affiliation:
Department of Pure Mathematics, Delft University of Technology, P.O. Box 5031, 2600 GA Delft, The Netherlands
Get access Rights & Permissions [Opens in a new window]

Extract

The Laplacian operator Δ on a bounded domain Ω in ℝn containing 0, with Dirichlet boundary condition, is perturbed by a pseudopotential δ, the Dirac measure at 0. Such a perturbation will be defined in Lp(ℝ) for n = 2, 1 <lt; p < ∞, and for n = 3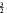, < p < 3, and is shown to be the generator of an analytic semigroup. Thus solutions of the corresponding evolutionary system are well defined. The necessary estimates involve the Gagliardo– Nirenberg inequality and the Kato inequality.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 124 , Issue 5 , 1994 , pp. 917 - 926
Copyright
Copyright © Royal Society of Edinburgh 1994

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Adams, R. A.. Sobolev Spaces (New York: Academic Press, 1975).Google Scholar
2Albeverio, S., Gesztesy, F., Høegh-Krohn, R. and Holden, H.. Solvable Models in Quantum Mechanics (New York: Springer, 1988).CrossRefGoogle Scholar
3Albeverio, S. and Seba, P.. Wave chaos in quantum systems with point interaction. J. Statist. Phys. 64(1991), 369–383.CrossRefGoogle Scholar
4Amann, H.. On abstract parabolic fundamental solutions. J. Math. Soc. Japan 39 (1987), 93–116.CrossRefGoogle Scholar
5Caspers, W.. On point interactions (Thesis, Delft University of Technology, 1992).Google Scholar
6Caspers, W. and Clément, Ph.. Point interactions in Lp. Semigroup Forum 46 (1993), 253–265.CrossRefGoogle Scholar
7van Diejen, J. F. and Tip, A.. Scattering from generalized point interactions using self-adjoint extensions in Pontryagin spaces. J. Math. Phys. 32 (1991), 630–641.CrossRefGoogle Scholar
8Fermi, E.. Sul moto dei neutroni nelle sostanze idrogenate. Ricerca Sci. 7 (1936), 13–52; English translation in E. Fermi Collected papers, Vol. I, Italy, 1921–1938, 980–1016 (Chicago: University of Chicago Press, 1962).Google Scholar
9Friedman, A.. Partial Differential Equations of Parabolic Type. (Englewood Cliffs, N.J.: Prentice-Hall, 1964).Google Scholar
10Greiner, G.. Perturbing the boundary conditions of a generator. Houston J. Math. 13 (1987), 213–229.Google Scholar
11Greiner, G. and Kuhn, K. G.. Linear and semilinear boundary conditions: The analytic case. In Semigroup Theory and Evolution Equations: The Second International Conference, eds. Clément, Ph., Mitidieri, E. and de Pagter, B. (New York: Marcel Dekker, 1991).Google Scholar
12Kato, T.. Schrödinger operators with singular potentials. Israel J. Math. 13 (1972), 135–148.CrossRefGoogle Scholar
13Lumer, G.. Principes du maximum paraboliques pour des domaines (x, t) non-cylindriques. Séminaire de Théorie du Potentiel, no. 8, Lecture Notes in Mathematics 1235, 105–113 (Berlin: Springer, 1987).CrossRefGoogle Scholar
14Pazy, A.. Semigroups of Linear Operators and Applications to Partial Differential Equations (Berlin: Springer, 1983).CrossRefGoogle Scholar
15Reed, M. and Simon, B.. Methods of Modern Mathematical Physics II: Fourier Analysis, Self-adjointness (New York: Academic Press, 1972).Google Scholar
16Shondin, Yu. G.. Quantum mechanical models in ℝN related with the extensions of energy operators in Pontrjagin spaces. Theoretical and Mathematical Physics 74–3 (1988), 331–344 (in Russian).Google Scholar
17Watson, G. N.. A Treatise on the Theory of Bessel Functions, 2nd edn (Edinburgh: Cambridge University Press, 1962).Google Scholar