Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-29T07:22:15.434Z Has data issue: false hasContentIssue false
  • English
  • Français

Perforation conditions and almost algebraic order in Cuntz semigroups

Part of: Lattices Selfadjoint operator algebras Special categories $K$-theory and operator algebras Basic linear algebra

Published online by Cambridge University Press:  18 April 2018

Ramon Antoine ,
Francesc Perera  and
Henning Petzka
Ramon Antoine
Affiliation:
Departament de Matemàtiques, Universitat Autònoma de Barcelona, 08193 Bellaterra, Barcelona, Spain ([email protected]; [email protected])
Francesc Perera
Affiliation:
Departament de Matemàtiques, Universitat Autònoma de Barcelona, 08193 Bellaterra, Barcelona, Spain ([email protected]; [email protected])
Henning Petzka
Affiliation:
Mathematisches Institut, Universität Münster, Einsteinstraße 62, 48149 Münster, Germany ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

For a C*-algebra A, determining the Cuntz semigroup Cu(A ⊗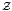) in terms of Cu(A) is an important problem, which we approach from the point of view of semigroup tensor products in the category of abstract Cuntz semigroups by analysing the passage of significant properties from Cu(A) to Cu(A)⊗Cu Cu(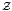). We describe the effect of the natural map Cu(A) → Cu(A)⊗Cu Cu(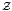) in the order of Cu(A), and show that if A has real rank 0 and no elementary subquotients, Cu(A)⊗Cu Cu(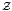) enjoys the corresponding property of having a dense set of (equivalence classes of) projections. In the simple, non-elementary, real rank 0 and stable rank 1 situation, our investigations lead us to identify almost unperforation for projections with the fact that tensoring with 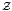is inert at the level of the Cuntz semigroup.

Keywords

Cuntz semigrouptensor productC*-algebra

MSC classification

Secondary: 06B35: Continuous lattices and posets, applications 15A69: Multilinear algebra, tensor products 46L05: General theory of $C^*$-algebras 46L35: Classifications of $C^*$-algebras 46L80: $K$-theory and operator algebras (including cyclic theory) 18B35: Preorders, orders and lattices (viewed as categories) 19K14: $K_0$ as an ordered group, traces 46L06: Tensor products of $C^*$-algebras
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 148 , Issue 4 , August 2018 , pp. 669 - 702
Copyright
Copyright © Royal Society of Edinburgh 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)