Published online by Cambridge University Press: 26 May 2009
We consider strictly quasiconvex integrals

in the multi-dimensional calculus of variations. For the C2-integrand f : ℝNn → ℝ we impose (p, q)-growth conditions
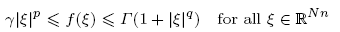
with γ, Γ > 0 and 1 < p ≤ q < min {p + 1/n, p(2n − 1)/(2n − 2)}. Under these assumptions we prove partial C1, αloc-regularity for strong local minimizers of F and the associated relaxed functional 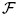 .
.