Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Philos, Ch. G.
1980.
Oscillatory and asymptotic behavior of strongly superlinear differential equations with deviating arguments.
Annali di Matematica Pura ed Applicata,
Vol. 126,
Issue. 1,
p.
343.
Granata, Antonio
1980.
Canonical Factorizations of Disconjugate Differential Operators.
SIAM Journal on Mathematical Analysis,
Vol. 11,
Issue. 1,
p.
160.
Philos, Ch. G.
1981.
On the existence of nonoscillatory solutions tending to zero at ? for differential equations with positive delays.
Archiv der Mathematik,
Vol. 36,
Issue. 1,
p.
168.
Philos, Ch. G.
Sficas, Y. G.
and
Staikos, V. A.
1982.
Some results on the asymptotic behavior of nonoscillatory solutions of differential equations with deviating arguments.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 32,
Issue. 3,
p.
295.
Philos, Ch.G.
and
Staikos, V.A.
1982.
A basic asymptotic criterion for differential equations with deviating arguments and its applications to the nonoscillation of linear ordinary equations.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 6,
Issue. 10,
p.
1095.
Philos, Ch. G.
1983.
On the Asymptotic Behavior of the Nonoscillatory Solutions of Differential Equations with Deviating Arguments.
Mathematische Nachrichten,
Vol. 113,
Issue. 1,
p.
107.
Agarwal, Ravi P.
1984.
General Inequalities 4.
Vol. 71,
Issue. ,
p.
95.
Kitamura, Yuichi
1985.
Oscillation of functional-differential equations with general deviating arguments.
Hiroshima Mathematical Journal,
Vol. 15,
Issue. 3,
Jaroš, Jaroslav
1986.
Oscillation criteria for functional-differential inequalities with strongly bounded forcing term.
Hiroshima Mathematical Journal,
Vol. 16,
Issue. 3,
Jaroš, Jaroslav
1987.
Maintenance of oscillations under the effect of a strongly bounded forcing term.
Hiroshima Mathematical Journal,
Vol. 17,
Issue. 2,
Karakostas, G.
and
Staikos, V.A.
1988.
μ-Like-continuous operators and some oscillation results.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 12,
Issue. 11,
p.
1149.
Bainov, D.D.
Dimitrova, M.B.
and
Myshkis, A.D.
1994.
Oscillatory and Asymptotic Properties of the Solutions of a Class of Operator-Differential Equations.
Rocky Mountain Journal of Mathematics,
Vol. 24,
Issue. 4,
Agarwal, Ravi P.
1995.
Sharp Opial-type inequalities involving $r$-derivatives and their applications.
Tohoku Mathematical Journal,
Vol. 47,
Issue. 4,
Agarwal, Ravi P.
and
Pang, Peter Y. H.
1995.
Opial Inequalities with Applications in Differential and Difference Equations.
p.
128.
Singh, Bhagat
2000.
On nonoscillation of canonical or noncanonical disconjugate functional equations.
Czechoslovak Mathematical Journal,
Vol. 50,
Issue. 3,
p.
627.


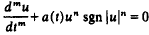 of the unknown function
of the unknown function