Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hsiang, Wu-Teh
and
Kwong, Man Kam
1982.
On the oscillation of nonlinear hyperbolic equations.
Journal of Mathematical Analysis and Applications,
Vol. 85,
Issue. 1,
p.
31.
Georgiou, D
and
Kreith, K
1985.
Functional characteristic initial value problems.
Journal of Mathematical Analysis and Applications,
Vol. 107,
Issue. 2,
p.
414.


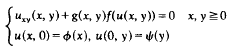
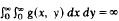 is not sufficient in the linear case.
is not sufficient in the linear case.