Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T17:54:52.663Z Has data issue: false hasContentIssue false
  • English
  • Français

On the swirling flow between rotating coaxial disks, asymptotic behaviour, II

Published online by Cambridge University Press:  14 November 2011

Heinz Otto Kreiss  and
Seymour V. Parter
Heinz Otto Kreiss
Affiliation:
California Institute of Technology, Pasadena, California, U.S.A
Seymour V. Parter
Affiliation:
University of Wisconsin-Madison, Madison, Wisconsin, U.S.A
Get access Rights & Permissions [Opens in a new window]

Synopsis

Consider solutions 〈H(x, ε), G(x, ε)〉 of the von Kármán equations for the swirling flow between two rotating coaxial disks

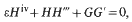
and

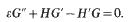
We assume that |H(x, ε)| + |Hʹ(x, ε)| + |G(x, ε)|≦B. This work considers shapes and asymptotic behaviour as ε→0+. We consider the type of limit functions 〈H(x), G(x)〉 that are permissible. In particular, if 〈H(x, ε), G(x, ε)〉 also satisfy the boundary conditions H(0, ε)=H(1, ε)=0, Hʹ(0, ε)=Hʹ(1, ε)=0 then H(x) has no simple zeros. That is, there does not exist a point Z ε [0, 1] such that H(x)=0, Hʹ(z)≠0. Moreover, the case of “cells” which oscillate is studied in detail.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 90 , Issue 3-4 , 1981 , pp. 317 - 346
Copyright
Copyright © Royal Society of Edinburgh 1981

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Batchelor, G. K.. Note on a class of solutions of the Navier–Stokes equations representing steady rotationally-symmetric flow. Quart. J. Mech. Appl. Math. 4 (1951), 29–41.CrossRefGoogle Scholar
2von Kármán, T.. Über laminare und turbulente Reibung. Z. Angew. Math. Mech. 1 (1921), 232–252.Google Scholar
3Kreiss, H. O.. Difference methods for stiff ordinary differential equations. SIAM J. Numer. Anal. 15 (1978), 21–58.CrossRefGoogle Scholar
4Kreiss, H. O. and Parter, S. V.. On the swirling flow between rotating coaxial disks, asymptotic behavior 1. MRC Report No. 1941 (1979).Google Scholar
5Landau, E.. Einige Ungleichung für zweimal differenzbare funktionen. Proc. London Math. Soc. 13 (1913), 43–49.Google Scholar
6McLeod, J. B.. A note on rotationally symmetric flow above an infinite rotating disc. Mathematika 17 (1970), 243–249.CrossRefGoogle Scholar
7McLeod, J. B. and Parter, S. V.. On the flow between two counter-rotating infinite plane disks. Arch. Rational Mech. Anal. 54 (1974), 301–327.CrossRefGoogle Scholar
8Mellor, G. L., Chapple, P. J. and Stokes, V. K.. On the flow between a rotating and a stationary disk. J. Fluid Mech. 31 (1968), 95–112.CrossRefGoogle Scholar
9Roberts, S. M. and Shipman, J. S.. Computation of the flow between a rotating and a stationary disk. J. Fluid Mech. 73 (1967), 53–63.CrossRefGoogle Scholar