Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-24T18:38:32.244Z Has data issue: false hasContentIssue false
  • English
  • Français

On the regularity of stochastic difference equations in hyperfinite-dimensional vector spaces and applications to 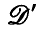-valued stochastic differential equations

Published online by Cambridge University Press:  14 November 2011

Jiang-Lun Wu
Jiang-Lun Wu
Affiliation:
Institute of Applied Mathematics, Academia Sinica, P.O. Box 2734, Beijing 100080, P.R. China
Get access Rights & Permissions [Opens in a new window]

Abstract

Nonstandard analysis is used, in this paper, to give a construction of a Wiener 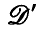-process Wt, t ∈ [0, ∞). From this, a hyperfinite representation of stochastic integrals for operatorvalued processes with respect to Wt is derived, and existence theorems in the spirit of Keisler are proved for (infinite-dimensional) stochastic differential equations of Itô's type one and a certain kind of Itô's type two, via regularity of hyperfinite stochastic difference equations.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 124 , Issue 6 , 1994 , pp. 1089 - 1117
Copyright
Copyright © Royal Society of Edinburgh 1994

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Albeverio, S., Fenstad, J. E., Høegh-Krohn, R. and Lindstrøm, T. L.. Nonstandard Methods in Stochastic Analysis and Mathematical Physics (New York: Academic Press, 1986).Google Scholar
2Chow, P. L.. Stochastic differential equations in infinite dimensions. In Mathematics & Physics, Vol. 3, ed. Streit, L., 179–220 (Singapore: World Scientific, 1989).Google Scholar
3Cutland, N. J.. Nonstandard measure theory and its applications. Bull. London Math. Soc. 15 (1983), 529–589.CrossRefGoogle Scholar
4Funaki, T.. Random motion of strings and stochastic differential equations on the space C([0,1], Rd). In Proceedings of the Taniguchi International Conference on Stochastic Analysis, 1982, 121–133 (Kyoto: Katata; Tokyo: Kinekuniya, 1984).Google Scholar
5Hida, T.. Brownian Motion (New York: Springer, 1980).CrossRefGoogle Scholar
6Ito, K.. Foundations of Stochastic Differential Equations in Infinite Dimensional Spaces, CBMS 47 (Philadelphia: SIAM, 1984).CrossRefGoogle Scholar
7Kallianpur, G. and Perez-Abreu, V.. Stochastic evolution equations driven by nuclear-space-valued martingales. Appl. Math. Optim. 17 (1988), 237–272.CrossRefGoogle Scholar
8Keisler, H. J.. Infinitesimals in probability theory. In Nonstandard Analysis and Its Applications, ed. Cutland, N. J., LMS Student Text 10, 106–139 (Cambridge: Cambridge University Press, 1988).CrossRefGoogle Scholar
9Lindstrem, T. L.. A Loeb measure approach to theorems by Prohorov, Sazonov and Gross. Trans. Amer. Math. Soc. 269 (1982), 521–543.CrossRefGoogle Scholar
10Lindstram, T. L.. Stochastic integration in hyperfinite dimensional linear spaces. In Nonstandard Analysis–Recent Development, ed. Hurd, A. E., Lecture Notes in Mathematics 983, 134–161 (Berlin: Springer, 1983).CrossRefGoogle Scholar
11Lindstram, T. L.. An invitation to nonstandard analysis. In Nonstandard Analysis and Its Applications, ed. Cutland, N. J., LMS Student Text 10, 1–105 (Cambridge: Cambridge University Press, 1988).Google Scholar
12Parisi, G. and Wu, Y. S.. Perturbation theory without gauge fixing. Scientia Sinica 24 (1981), 483–496.Google Scholar
13Ramer, R.. On nonlinear transformations of Gaussian measures. J. Fund. Anal. 15 (1974), 166–187.CrossRefGoogle Scholar
14Yosida, K.. Functional Analysis, 4th edn (Berlin: Springer, 1978).CrossRefGoogle Scholar