Hostname: page-component-6bf8c574d5-2jptb Total loading time: 0 Render date: 2025-02-17T12:57:34.523Z Has data issue: false hasContentIssue false
  • English
  • Français

On the optimization of the first weighted eigenvalue

Part of: Variational methods for eigenvalues of operators Spectral theory and eigenvalue problems Partial differential equations Equations of mathematical physics and other areas of application Existence theories

Published online by Cambridge University Press:  12 September 2022

Nirjan Biswas Open the ORCID record for Nirjan Biswas [Opens in a new window] ,
Ujjal Das Open the ORCID record for Ujjal Das [Opens in a new window]  and
Mrityunjoy Ghosh
Nirjan Biswas
Affiliation:
Tata Institute of Fundamental Research, Centre For Applicable Mathematics, Post Bag No 6503, Sharada Nagar, Bangalore, 560065, India ([email protected])
Ujjal Das
Affiliation:
Department of Mathematics, Technion - Israel Institute of Technology, Haifa, 32000, Israel ([email protected])
Mrityunjoy Ghosh
Affiliation:
Department of Mathematics, Indian Institute of Technology Madras, Chennai, 600036, India ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

For $N\geq 2$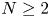, a bounded smooth domain $\Omega$ 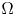in $\mathbb {R}^{N}$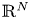, and $g_0,\, V_0 \in L^{1}_{loc}(\Omega )$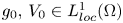, we study the optimization of the first eigenvalue for the following weighted eigenvalue problem:

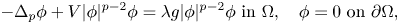
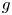\[ -\Delta_p \phi + V |\phi|^{p-2}\phi = \lambda g |\phi|^{p-2}\phi \text{ in } \Omega, \quad \phi=0 \text{ on } \partial \Omega, \]
where $g$ and $V$ 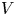vary over the rearrangement classes of $g_0$ 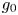and $V_0$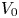, respectively. We prove the existence of a minimizing pair $(\underline {g},\,\underline {V})$ 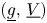and a maximizing pair $(\overline {g},\,\overline {V})$ 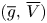for $g_0$ 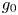and $V_0$ 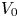lying in certain Lebesgue spaces. We obtain various qualitative properties such as polarization invariance, Steiner symmetry of the minimizers as well as the associated eigenfunctions for the case $p=2$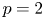. For annular domains, we prove that the minimizers and the corresponding eigenfunctions possess the foliated Schwarz symmetry.

Keywords

Optimization of the principal eigenvaluepolarization invarianceSchwarz symmetrySteiner symmetryfoliated Schwarz symmetry

MSC classification

Primary: 35B06: Symmetries, invariants, etc. 49J30: Optimal solutions belonging to restricted classes (Lipschitz controls, bang-bang controls, etc.) 35P15: Estimation of eigenvalues, upper and lower bounds 35Q93: PDEs in connection with control and optimization 49R05: Variational methods for eigenvalues of operators (should also be assigned at least one other classification number in Section 49)
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 153 , Issue 6 , December 2023 , pp. 1777 - 1804
Check for updates
Copyright
Copyright © The Author(s), 2022. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Allegretto, W. and Huang, Y. X.. A Picone's identity for the $p$-Laplacian and applications. Nonlinear Anal. 32 (1998), 819–830.CrossRefGoogle Scholar
Anedda, C. and Cuccu, F.. Steiner symmetry in the minimization of the first eigenvalue in problems involving the $p$-Laplacian. Proc. Amer. Math. Soc. 144 (2016), 3431–3440.CrossRefGoogle Scholar
Anoop, T. V.. Weighted eigenvalue problems for the $p$-Laplacian with weights in weak Lebesgue spaces. Electron. J. Differ. Equ. 64 (2011), 222011.Google Scholar
Anoop, T. V., Ashok Kumar, K. and Kesavan, S.. A shape variation result via the geometry of eigenfunctions. J. Differ. Equ. 298 (2021), 430–462.CrossRefGoogle Scholar
Anoop, T. V., Lucia, M. and Ramaswamy, M.. Eigenvalue problems with weights in Lorentz spaces. Calc. Var. Partial Differ. Equ. 36 (2009), 355–376.CrossRefGoogle Scholar
Ashbaugh, M. S. and Harrell, E. M.. II. Maximal and minimal eigenvalues and their associated nonlinear equations. J. Math. Phys. 28 (1987), 1770–1786.CrossRefGoogle Scholar
Berestycki, H., Hamel, F. and Roques, L.. Analysis of the periodically fragmented environment model. I. Species persistence. J. Math. Biol. 51 (2005), 75–113.CrossRefGoogle ScholarPubMed
Bianchi, G., Gardner, R. J., Gronchi, P. and Kiderlen, M.. Rearrangement and polarization. Adv. Math. 374 (2020), 107380.CrossRefGoogle Scholar
Brezis, H. and Ponce, A. C.. Remarks on the strong maximum principle. Differ. Integral Equ. 16 (2003), 1–12.Google Scholar
Brock, F.. Symmetry and monotonicity of solutions to some variational problems in cylinders and annuli. Electron. J. Differential Equations 108 (2003), 1–20.Google Scholar
Brock, F.. Positivity and radial symmetry of solutions to some variational problems in $\Bbb R^{N}$. J. Math. Anal. Appl. 296 (2004), 226–243.CrossRefGoogle Scholar
Brock, F., Croce, G., Guibé, O. and Mercaldo, A.. Symmetry and asymmetry of minimizers of a class of noncoercive functionals. Adv. Calc. Var. 13 (2020), 15–32.CrossRefGoogle Scholar
Brock, F. and Solynin, A. Y.. An approach to symmetrization via polarization. Trans. Amer. Math. Soc. 352 (2000), 1759–1796.CrossRefGoogle Scholar
Brothers, J. E. and Ziemer, W. P.. Minimal rearrangements of Sobolev functions. J. Reine Angew. Math. 384 (1988), 153–179.Google Scholar
Burton, G. R.. Variational problems on classes of rearrangements and multiple configurations for steady vortices. Ann. Inst. H. Poincaré Anal. Non Linéaire 6 (1989), 295–319.CrossRefGoogle Scholar
Cadeddu, L. and Porru, G., Symmetry breaking in problems involving semilinear equations. Discrete Contin. Dyn. Syst., (Dynamical systems, differential equations and applications. 8th AIMS Conference. Suppl. Vol. I):219–228, 2011.Google Scholar
Cantrell, R. S. and Cosner, C.. Diffusive logistic equations with indefinite weights: population models in disrupted environments. Proc. Roy. Soc. Edinburgh Sect. A 112 (1989), 293–318.CrossRefGoogle Scholar
Cantrell, R. S. and Cosner, C.. Diffusive logistic equations with indefinite weights: population models in disrupted environments. II. SIAM J. Math. Anal. 22 (1991), 1043–1064.CrossRefGoogle Scholar
Chanillo, S., Grieser, D., Imai, M., Kurata, K. and Ohnishi, I.. Symmetry breaking and other phenomena in the optimization of eigenvalues for composite membranes. Comm. Math. Phys. 214 (2000), 315–337.CrossRefGoogle Scholar
Cianchi, A. and Fusco, N.. Steiner symmetric extremals in Pólya-Szegö type inequalities. Adv. Math. 203 (2006), 673–728.CrossRefGoogle Scholar
Cox, S. J. and McLaughlin, J. R.. Extremal eigenvalue problems for composite membranes, I, II.. Appl. Math. Optim. 22 (1990), 153–167.CrossRefGoogle Scholar
Cuccu, F., Emamizadeh, B. and Porru, G.. Optimization of the first eigenvalue in problems involving the $p$-Laplacian. Proc. Amer. Math. Soc. 137 (2009), 1677–1687.CrossRefGoogle Scholar
Cuccu, F. and Porru, G.. Optimization in a problem of heat conduction. Adv. Math. Sci. Appl. 12 (2002), 245–255.Google Scholar
Cuesta, M. and Ramos Quoirin, H.. A weighted eigenvalue problem for the $p$-Laplacian plus a potential. NoDEA Nonlinear Differ. Equ. Appl. 16 (2009), 469–491.CrossRefGoogle Scholar
Damascelli, L. and Pardo, R.. A priori estimates for some elliptic equations involving the $p$-Laplacian. Nonlinear Anal. Real World Appl. 41 (2018), 475–496.CrossRefGoogle Scholar
Del Pezzo, L. M. and Fernández Bonder, J.. An optimization problem for the first weighted eigenvalue problem plus a potential. Proc. Amer. Math. Soc. 138 (2010), 3551–3567.CrossRefGoogle Scholar
Derlet, A., Gossez, J.-P. and Takáč, P.. Minimization of eigenvalues for a quasilinear elliptic Neumann problem with indefinite weight. J. Math. Anal. Appl. 371 (2010), 69–79.CrossRefGoogle Scholar
Emamizadeh, B. and Prajapat, J. V.. Symmetry in rearrangement optimization problems. Electron. J. Differential Equations 149 (2009), 1–10.Google Scholar
Fernández Bonder, J. and Del Pezzo, L. M.. An optimization problem for the first eigenvalue of the $p$-Laplacian plus a potential. Commun. Pure Appl. Anal. 5 (2006), 675–690.CrossRefGoogle Scholar
Guedda, M. and Véron, L.. Quasilinear elliptic equations involving critical Sobolev exponents. Nonlinear Anal. 13 (1989), 879–902.CrossRefGoogle Scholar
Henrot, A., Extremum problems for eigenvalues of elliptic operators. Frontiers in Mathematics. (Birkhäuser Verlag, Basel, 2006).CrossRefGoogle Scholar
Jha, K. and Porru, G.. Minimization of the principal eigenvalue under Neumann boundary conditions. Numer. Funct. Anal. Optim. 32 (2011), 1146–1165.CrossRefGoogle Scholar
Kawohl, B., Rearrangements and convexity of level sets in PDE, volume 1150 of Lecture Notes in Mathematics (Springer-Verlag, Berlin, 1985).CrossRefGoogle Scholar
Kawohl, B., Lucia, M. and Prashanth, S.. Simplicity of the principal eigenvalue for indefinite quasilinear problems. Adv. Differ. Equ. 12 (2007), 407–434.Google Scholar
Krein, M. G.. On certain problems on the maximum and minimum of characteristic values and on the Lyapunov zones of stability. Amer. Math. Soc. Transl. (2) 1 (1955), 163–187.Google Scholar
Kurata, K., Shibata, M. and Sakamoto, S.. Symmetry-breaking phenomena in an optimization problem for some nonlinear elliptic equation. Appl. Math. Optim. 50 (2004), 259–278.CrossRefGoogle Scholar
Lamboley, J., Laurain, A., Nadin, G. and Privat, Y.. Properties of optimizers of the principal eigenvalue with indefinite weight and Robin conditions. Calc. Var. Partial Differential Equations 55 (2016), 144.CrossRefGoogle Scholar
Leadi, L. and Yechoui, A.. Principal eigenvalue in an unbounded domain with indefinite potential. NoDEA Nonlinear Differ. Equ. Appl. 17 (2010), 391–409.CrossRefGoogle Scholar
Lieberman, G. M.. Boundary regularity for solutions of degenerate elliptic equations. Nonlinear Anal. 12 (1988), 1203–1219.CrossRefGoogle Scholar
Mazari, I., Nadin, G. and Privat, Y.. Optimal location of resources maximizing the total population size in logistic models. J. Math. Pures Appl. (9) 134 (2020), 1–35.CrossRefGoogle Scholar
Mazzoleni, D., Pellacci, B. and Verzini, G.. Asymptotic spherical shapes in some spectral optimization problems. J. Math. Pures Appl. (9) 135 (2020), 256–283.CrossRefGoogle Scholar
Pielichowski, W. a.. The optimization of eigenvalue problems involving the $p$-Laplacian. Univ. Iagel. Acta Math. 42 (2004), 109–122.Google Scholar
Sciunzi, B.. Regularity and comparison principles for $p$-Laplace equations with vanishing source term. Commun. Contemp. Math. 16 (2014), 1450013.CrossRefGoogle Scholar
Skellam, J. G.. Random dispersal in theoretical populations. Biometrika 38 (1951), 196–218.CrossRefGoogle ScholarPubMed
Szulkin, A. and Willem, M.. Eigenvalue problems with indefinite weight. Studia Math. 135 (1999), 191–201.Google Scholar
Van Schaftingen, J.. Symmetrization and minimax principles. Commun. Contemp. Math. 7 (2005), 463–481.CrossRefGoogle Scholar
Weth, T.. Symmetry of solutions to variational problems for nonlinear elliptic equations via reflection methods. Jahresber. Dtsch. Math.-Ver. 112 (2010), 119–158.CrossRefGoogle Scholar