Hostname: page-component-6bf8c574d5-8gtf8 Total loading time: 0 Render date: 2025-02-28T10:00:07.007Z Has data issue: false hasContentIssue false
  • English
  • Français

On the global existence of solutions to chemotaxis system for two populations in dimension two

Part of: Physiological, cellular and medical topics Partial differential equations

Published online by Cambridge University Press:  09 January 2023

Ke Lin
Ke Lin*
Affiliation:
School of Mathematics, Southwestern University of Economics and Finance, Chengdu, 611130 Sichuan, China ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the global existence for the following fully parabolic chemotaxis system with two populations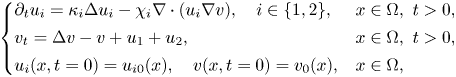

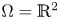\[\left\{ \begin{array}{@{}ll} \partial_tu_i=\kappa_i\Delta u_i-\chi_i\nabla\cdot(u_i\nabla v),\quad i\in\{1,2\}, & x\in\Omega,\ t>0, \\ v_t=\Delta v-v+u_1+u_2, & x\in\Omega,\ t>0,\\ u_i(x,t=0)=u_{i0}(x),\quad v(x,t=0)=v_0(x), & x\in\Omega, \end{array} \right. \]
where $\Omega =\mathbb {R}^2$ or $\Omega =B_R(0)\subset \mathbb {R}^2$ 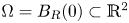supplemented with homogeneous Neumann boundary conditions, $\kappa _i,\chi _i>0,$ 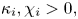$i=1,2$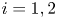. The global existence remains open for the fully parabolic case as far as the author knows, while the existence of global solution was known for the parabolic-elliptic reduction with the second equation replaced by $0=\Delta v-v+u_1+u_2$ 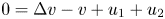or $0=\Delta v+u_1+u_2$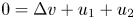. In this paper, we prove that there exists a global solution if the initial masses satisfy the certain sub-criticality condition. The proof is based on a version of the Moser–Trudinger type inequality for system in two dimensions.

Keywords

Chemotaxisglobal solutionthe Moser–Trudinger inequality for system

MSC classification

Primary: 35A01: Existence problems
Secondary: 92C17: Cell movement (chemotaxis, etc.)
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 153 , Issue 6 , December 2023 , pp. 2106 - 2128
Check for updates
Copyright
Copyright © The Author(s), 2023. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alikakos, N. D.. $L^p$ bounds of solutions of reaction-diffusion equations. Commun. Partial Differ. Equ. 4 (1979), 827–868.CrossRefGoogle Scholar
Biler, P.. Local and global solvability to some parabolic-elliptic systems of chemotaxis. Adv. Math. Sci. Appl. 8 (1998), 715–743.Google Scholar
Calvez, V. and Corrias, L.. The parabolic-parabolic Keller–Segel model in $\mathbb {R}^2$. Commun. Math. Sci. 6 (2008), 417–447.CrossRefGoogle Scholar
Chipot, M., Shafrir, I. and Wolansky, G.. On the solutions of Liouville systems. J. Differ. Equ. 140 (1997), 59–105.CrossRefGoogle Scholar
Conca, C., Espejo, E. and Vilches, K.. Remarks on the blowup and global existence for a two species chemotactic Keller–Segel system in $\mathbb {R}^2$. Eur. J. Appl. Math. 22 (2011), 553–580.CrossRefGoogle Scholar
Diaz, J. I., Nagai, T. and Rakotoson, J. M.. Symmetrization techniques on unbounded domains: application to a chemotaxis system on $\mathbb {R}^n$. J. Differ. Equ. 145 (1998), 156–183.CrossRefGoogle Scholar
Espejo, E., Stevens, A. and Velzquez, J.. Simultaneous finite time blow-up in a two-species model for chemotaxis. Analysis (Munich) 29 (2009), 317–338.Google Scholar
Espejo, E., Vilches, K. and Conca, C.. Sharp condition for blow-up and global existence in a two species chemotactic Keller–Segel system in $\mathbb {R}^2$. Eur. J. Appl. Math. 24 (2013), 297–313.CrossRefGoogle Scholar
Espejo, E., Vilches, K. and Conca, C.. A simultaneous blow-up problem arising in tumor modeling. J. Math. Biol. 79 (2019), 1357–1399.CrossRefGoogle ScholarPubMed
Herrero, M. A. and Velázquez, J. J. L.. A blow-up mechanism for a chemotaxis model. Ann. Scoula Norm. Sup. Pisa IV 35 (1997), 633–683.Google Scholar
Horstmann, D.. From 1970 until present: the Keller–Segel model in chemotaxis and its consequences. I. Jahresber. Deutsch. Math. Verein. 105 (2003), 103–165.Google Scholar
Horstmann, D.. Generalizing the Keller–Segel model: Lyapunov functionals, steady state analysis, and blow-up results for multi-species chemotaxis models in the presence of attraction and repulsion between competitive interacting species. J. Nonlinear Sci. 21 (2011), 231–270.CrossRefGoogle Scholar
Jäger, W. and Luckhaus, S.. On explosions of solutions to a system of partial differential equations modeling chemotaxis. Trans. Amer. Math. Soc. 329 (1992), 819–824.CrossRefGoogle Scholar
Keller, E. F. and Segel, L. A.. Initiation of slime mold aggregation viewed as an instability. J. Theor. Biol. 26 (1970), 399–415.CrossRefGoogle ScholarPubMed
Mizoguchi, N.. Global existence for the Cauchy problem of the parabolic-parabolic Keller–Segel system on the plane. Calc. Var. Partial Differ. Equ. 48 (2013), 491–505.CrossRefGoogle Scholar
Moser, J.. A sharp form of an inequality by N. Trudinger. Indiana Univ. Math. J. 20 (1971), 1077–1092.CrossRefGoogle Scholar
Nagai, T.. Blow-up of radially symmetric solutions to a chemotaxis system. Adv. Math. Sci. Appl. 5 (1995), 581–601.Google Scholar
Nagai, T.. Blowup of nonradial solutions to parabolic-elliptic systems modeling chemotaxis in two dimensional domains. J. Inequal. Appl. 6 (2001), 37–55.Google Scholar
Nagai, T.. Global existence and decay estimates of solutions to a parabolic-elliptic system of drift-diffusion type in $\mathbb {R}^2$. Differ. Integral Equ. 24 (2010), 29–68.Google Scholar
Nagai, T. and Ogawa, T.. Brezis–Merle inequalities and application to the global existence of the Cauchy problem of the Keller–Segel system. Commun. Contemp. Math. 13 (2011), 795–812.CrossRefGoogle Scholar
Nagai, T., Senba, T. and Yoshida, K.. Application of the Trudinger–Moser inequality to a parabolic system of chemotaxis. Funkc. Ekvacioj 40 (1997), 411–433.Google Scholar
Shafrir, I. and Wolansky, G.. Moser–Trudinger type inequalities for systems in two dimensions. C. R. Acad. Sci. Paris Ser. I Math. 333 (2001), 439–443.CrossRefGoogle Scholar
Shafrir, I. and Wolansky, G.. Moser–Trudinger and logarithmic HLS inequalities for systems. J. Eur. Math. Soc. 7 (2005), 413–448.CrossRefGoogle Scholar
Tao, Y. and Winkler, M.. Energy-type estimates and global solvability in a two-dimensional chemotaxis-haptotaxis model with remodeling of non-diffusible attractant. J. Differ. Equ. 257 (2014), 784–815.CrossRefGoogle Scholar
Wolansky, G.. Multi-components chemotactic system in absence of conflicts. Eur. J. Appl. Math. 13 (2002), 641–661.CrossRefGoogle Scholar