Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Landes, Rüdiger
1985.
On weak solutions of quasilinear parabolic equations.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 9,
Issue. 9,
p.
887.
Landes, Rüdiger
and
Mustonen, Vesa
1987.
A strongly nonlinear parabolic initial boundary value problem.
Arkiv för Matematik,
Vol. 25,
Issue. 1-2,
p.
29.
Dubinskii, Yu. A.
1991.
High order nonlinear parabolic equations.
Journal of Soviet Mathematics,
Vol. 56,
Issue. 4,
p.
2557.
Scarpellini, B.
1994.
Bounded solutions of parabolic equations in unbounded domains.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 22,
Issue. 5,
p.
625.
Landes, Rüdiger
and
Mustonen, Vesa
1994.
On parabolic initial-boundary value problems with critical growth for the gradient.
Annales de l'Institut Henri Poincaré C, Analyse non linéaire,
Vol. 11,
Issue. 2,
p.
135.
Boccardo, Lucio
Dall'Aglio, Andrea
Gallouët, Thierry
and
Orsina, Luigi
1997.
Nonlinear Parabolic Equations with Measure Data.
Journal of Functional Analysis,
Vol. 147,
Issue. 1,
p.
237.
Miettinen, M.
and
Panagiotopoulos, P.D.
1999.
On parabolic hemivariational inequalities and applications.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 35,
Issue. 7,
p.
885.
Porretta, Alessio
1999.
Existence results for nonlinear parabolic equations via strong convergence of truncations.
Annali di Matematica Pura ed Applicata,
Vol. 177,
Issue. 1,
p.
143.
Blanchard, Dominique
Murat, François
and
Redwane, Hicham
2001.
Existence and Uniqueness of a Renormalized Solution for a Fairly General Class of Nonlinear Parabolic Problems.
Journal of Differential Equations,
Vol. 177,
Issue. 2,
p.
331.
Andreu, F.
Segura de León, S.
and
Toledo, J.
2004.
Quasi-linear diffusion equations with gradient terms and L1 data.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 56,
Issue. 8,
p.
1175.
Blanchard, D.
and
Porretta, A.
2005.
Stefan problems with nonlinear diffusion and convection.
Journal of Differential Equations,
Vol. 210,
Issue. 2,
p.
383.
Dall'Aglio, A.
Giachetti, D.
Leone, C.
and
Segura de León, S.
2006.
Quasi-linear parabolic equations with degenerate coercivity having a quadratic gradient term.
Annales de l'Institut Henri Poincaré C, Analyse non linéaire,
Vol. 23,
Issue. 1,
p.
97.
Azelmat, K.
Kbiri Alaoui, M.
Meskine, D.
and
Souissi, A.
2006.
Parabolic inequalities in L1 as limits of renormalized equations.
International Journal of Mathematics and Mathematical Sciences,
Vol. 2006,
Issue. 1,
BENDAHMANE, MOSTAFA
KARLSEN, KENNETH H.
and
URBANO, JOSÉ MIGUEL
2007.
ON A TWO-SIDEDLY DEGENERATE CHEMOTAXIS MODEL WITH VOLUME-FILLING EFFECT.
Mathematical Models and Methods in Applied Sciences,
Vol. 17,
Issue. 05,
p.
783.
Sbihi, Karima
and
Wittbold, Petra
2007.
Existence de solutions renormalisées pour un problème de Stefan non linéaire.
Comptes Rendus. Mathématique,
Vol. 345,
Issue. 11,
p.
629.
Blanchard, Dominique
Guibé, Olivier
and
Redwane, Hicham
2008.
Nonlinear equations with unbounded heat conduction and integrable data.
Annali di Matematica Pura ed Applicata,
Vol. 187,
Issue. 3,
p.
405.
Petitta, Francesco
2008.
Renormalized solutions of nonlinear parabolic equations with general measure data.
Annali di Matematica Pura ed Applicata,
Vol. 187,
Issue. 4,
p.
563.
Andreu, F.
Igbida, N.
Mazón, J.M.
and
Toledo, J.
2008.
Renormalized solutions for degenerate elliptic–parabolic problems with nonlinear dynamical boundary conditions andL1-data.
Journal of Differential Equations,
Vol. 244,
Issue. 11,
p.
2764.
Liqin, Zhang
and
Junning, Zhao
2009.
Existence and uniqueness of renormalized solutions for a class of degenerate parabolic equations.
Acta Mathematica Scientia,
Vol. 29,
Issue. 2,
p.
251.
Zhang, Chao
and
Zhou, Shulin
2010.
Renormalized and entropy solutions for nonlinear parabolic equations with variable exponents and L1 data.
Journal of Differential Equations,
Vol. 248,
Issue. 6,
p.
1376.


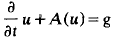 has weak solutions.
has weak solutions.