Hostname: page-component-f554764f5-wjqwx Total loading time: 0 Render date: 2025-04-20T10:42:34.065Z Has data issue: false hasContentIssue false
  • English
  • Français

On the existence of a nodal solution for p-Laplacian equations depending on the gradient

Part of: Elliptic equations and systems

Published online by Cambridge University Press:  31 January 2024

F. Faraci  and
D. Puglisi
F. Faraci
Affiliation:
Department of Mathematics and Computer Sciences, University of Catania, 95125 Catania, Italy ([email protected], [email protected])
D. Puglisi
Affiliation:
Department of Mathematics and Computer Sciences, University of Catania, 95125 Catania, Italy ([email protected], [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

In the present paper we deal with a quasi-linear elliptic equation depending on a sublinear nonlinearity involving the gradient. We prove the existence of a nontrivial nodal solution employing the theory of invariant sets of descending flow together with sub-supersolution techniques, gradient regularity arguments, strong comparison principle for the $p$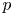-Laplace operator. The same conclusion is obtained for an eigenvalue problem under a different set of assumptions.

Keywords

p-Laplace operatorgradient dependencenodal solutiongradient flow

MSC classification

Primary: 35J60: Nonlinear elliptic equations
Secondary: 35J92: Quasilinear elliptic equations with $p$-Laplacian
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , First View , pp. 1 - 22
Check for updates
Copyright
Copyright © The Author(s), 2024. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Amann, H. and Crandall, M. G.. On some existence theorems for semi-linear elliptic equations. Indiana Univ. Math. J. 27 (1978), 779–790.CrossRefGoogle Scholar
Arcoya, D. and Ruiz, D.. The Ambrosetti–Prodi problem for the $p$-Laplacian operator. Commun. Partial Differ. Equ. 31 (2006), 849–865.CrossRefGoogle Scholar
Bartsch, T. and Liu, Z.. Multiple sign changing solutions of a quasilinear elliptic eigenvalue problem involving the $p$-Laplacian. Commun. Contemp. Math. 6 (2004), 245–258.CrossRefGoogle Scholar
Bartsch, T. and Liu, Z.. On a superlinear elliptic $p$-Laplacian equation. J. Differ. Equ. 198 (2004), 149–175.CrossRefGoogle Scholar
Bartsch, T., Liu, Z. and Weth, T.. Nodal solutions of $p$-Laplacian equation. Proc. London Math. Soc. 91 (2005), 129–152.CrossRefGoogle Scholar
Bartsch, T. and Wang, Z.-Q.. On the existence of sign changing solutions for semilinear Dirichlet problems. Topol. Methods Nonlinear Anal. 7 (1996), 115–131.CrossRefGoogle Scholar
Boccardo, L., Gallouët, T. and Orsina, L.. Existence and nonexistence of solutions for some nonlinear elliptic equations. J. Anal. Math. 73 (1997), 203–223.CrossRefGoogle Scholar
Carl, S. and Perera, K.. Sign-changing and multiple solutions for the $p$-Laplacian. Abstr. Appl. Anal. 7 (2002), 613–625.CrossRefGoogle Scholar
Cianchi, A. and Maz'ya, V.. Gradient regularity via rearrangements for p-Laplacian type elliptic boundary value problems. J. Eur. Math. Soc. 16 (2014), 571–595.Google Scholar
Damascelli, L.. Comparison theorems for some quasilinear degenerate elliptic operators and applications to symmetry and monotonicity results. Ann. Inst. H. Poincaré. Anal. Non Linéaire 15 (1998), 493–516.CrossRefGoogle Scholar
Dancer, E. N. and Du, Y.. On sign-changing solutions of certain semilinear elliptic problems. Appl. Anal. 56 (1995), 193–206.CrossRefGoogle Scholar
De Figueiredo, D., Girardi, M. and Matzeu, M.. Semilinear elliptic equations with dependence on the gradient via mountain-pass techniques. Differ. Integr. Equ. 17 (2004), 119–126.Google Scholar
Faraci, F., Motreanu, D. and Puglisi, D.. Positive solutions of quasi-linear elliptic equations with dependence on the gradient. Calc. Var. Partial Differ. Equ. 54 (2015), 525–538.CrossRefGoogle Scholar
Faraci, F. and Puglisi, D.. A singular semilinear problem with dependence on the gradient. J. Differ. Equ. 260 (2016), 3327–3349.CrossRefGoogle Scholar
Faraci, F. and Puglisi, D.. Nodal solutions of semi-linear elliptic equations with dependence on the gradient. Bull. Sci. Math. 175 (2022), 103101.CrossRefGoogle Scholar
Ladyzhenskaya, O. A. and Uraltseva, N. N.. Linear and quasilinear elliptic equations (New York–London: Academic Press, 1968).Google Scholar
Lieberman, G. M.. Boundary regularity for solutions of degenerate elliptic equations. Nonlinear Anal. 12 (1988), 1203–1219.CrossRefGoogle Scholar
Liu, G., Shi, S. and Wei, Y.. Sign-changing solutions for semilinear elliptic equations with dependence on the gradient via the Nehari method. Mediterr. J. Math. 14 (2017), 144.CrossRefGoogle Scholar
Liu, Z. and Sun, J.. Invariant sets of descending flow in critical point theory with applications to nonlinear differential equations. J. Differ. Equ. 172 (2001), 257–299.CrossRefGoogle Scholar
Pohožaev, S. I.. Equations of the type $\Delta u=f(x,u,Du)$ (Russian). Mat. Sb. (N.S.) 113 (1980), 324–338.Google Scholar
Ruiz, D.. A priori estimates and existence of positive solutions for strongly nonlinear problems. J. Differ. Equ. 199 (2004), 96–114.CrossRefGoogle Scholar
Sun, J. and Sun, J.. Existence theorems of multiple critical points and applications. Nonlinear Anal. 61 (2005), 1303–1317.CrossRefGoogle Scholar
Vázquez, J. L.. A strong maximum principle for some quasilinear elliptic equations. Appl. Math. Optim. 12 (1984), 191–202.CrossRefGoogle Scholar
Zhang, Z. and Li, S.. On sign-changing and multiple solutions of the $p$-Laplacian. J. Funct. Anal. 197 (2003), 447–468.CrossRefGoogle Scholar