No CrossRef data available.
Article contents
On the domains of minimal and maximal operators for regularisable singular differential expressions
Published online by Cambridge University Press: 14 November 2011
Synopsis
Certain classical differential expressions which are singular at a finite end-point (or at an interior point) can be represented as regular, scalar quasi-differential expressions, the best-known examples being the Boyd Equation and Laplace Tidal Wave Equation. We show here that in all such cases the domains of the minimal and maximal operators in the appropriate weighted Hilbert space 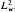 , for the regularised expression, coincide with the corresponding domains for the expression in its original, singular form.
, for the regularised expression, coincide with the corresponding domains for the expression in its original, singular form.
This is contrasted with a known property of the corresponding expression domains. Whereas for an expression M, the operator domains contain only functions y for which both y and My lie in the appropriate Hilbert space, the expression domain comprises a much larger set of functions with no such restrictions beyond those necessary for My to exist as a function. In the second-order case, the expression domain of the regularisation of a singular expression is known to be a strict subset of the original expression domain, contrasting with the results proved here for the operator domains.
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 121 , Issue 3-4 , 1992 , pp. 191 - 202
- Copyright
- Copyright © Royal Society of Edinburgh 1992


