Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-12-05T02:12:24.306Z Has data issue: false hasContentIssue false
  • English
  • Français

On the convolution operators arising in the study of abstract initial boundary value problems

Published online by Cambridge University Press:  14 November 2011

I. Alonso-Mallo  and
C. Palencia
I. Alonso-Mallo
Affiliation:
Departamento de Matemática Aplicada y Computatión, Universidad de Valladolid, Vallodolid, Spain
C. Palencia
Affiliation:
Departamento de Matemática Aplicada y Computatión, Universidad de Valladolid, Vallodolid, Spain e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

We consider convolution operators arising in the study of abstract initial boundary value problems. These operators are of the form

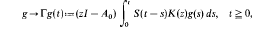
where {S(t)}t ≧0 is a C0-semigroup in a Banach space X,, with infinitesimal generator A0,: D(A0), ⊂ X, → X, and K(z): Y → X is a linxear, continuous mapping defined in another Banach space Y., We study the continuity of T between the spaces Lp([0, + ∞), Y), and Lq([0, + ∞), X), 1 ≦ p, q, ≦ + ∞. We give several examples of the applicability of the results to some familiar initial boundary value problems, including both parabolic and hyperbolic cases.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 126 , Issue 3 , 1996 , pp. 515 - 539
Copyright
Copyright © Royal Society of Edinburgh 1996

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Amann, H.. Semigroups and nonlinear evolution operators. Linear Algebra Appl., 84 (1986), 3–32.Google Scholar
2Cannarsa, P. and Vespri, V.. On maximal LP, regularity for the abstract Cauchy problem. Boll. Un., Mat. Ital., 6(1986), 165–75.Google Scholar
3Clement, Ph., Hijmans, H. J. A. M. et al. One Parameter Semigroups, (Amsterdam: North-Holland, 1987).Google Scholar
4Desch, W., Lasiecka, I. and Schappacher, W.. Feedback boundary control problems for linear semigroups. Israel J. Math., 51 (1985), 177–207.CrossRefGoogle Scholar
5Desch, W. and Schappacher, W. Some generation results for perturbed semigroups. In Semigroup, Theory and Applications, eds Clément, Ph. et al. , Lecture Notes in Pure and Applied Mathematics 116 (New York: Marcel Dekker, 1988).Google Scholar
6Diestel, J. and Ulh, J. J. Jr. Vector Measures, Mathematical Surveys 15 (Providence, RI: American Mathematical Society, 1977).Google Scholar
7Greiner, G.. Semilinear boundary conditions forevolution equations of hyperbolic type. In Semigroup, Theory and Applications,, eds Clément, Ph. et al. , Lecture Notes in Pure and Applied Mathematics 116 (New York: Marcel Dekker, 1988).Google Scholar
8Kreiss, H. O.. Initial boundary value problems for hyperbolic equations. Comm. Pure Appl. Math., 13 (1970), 277–98.Google Scholar
9Lasiecka, I.. Unified theory for abstract parabolic boundary problems—A semigroup approach. Appl., Math. Optim., 6 (1980), 287–333.Google Scholar
10Lasiecka, I.. Galerkin approximations of abstract parabolic boundary value problems with rough boundary data—Lp, theory. Math. Comp., 47 (1986), 55–75.Google Scholar
11Lasiecka, I. and Triggiani, R.. A lifting theorem for the time regularity of solutions to abstract equations with unbounded operators and applications to hyperbolic equations. Proc. Amer. Math., Soc., 104(1988), 745–55.CrossRefGoogle Scholar
12Lions, J. L.. Contrôlabilité Exacte, Perturbations et Stabilisation de Systèmes Distribués, (Tome 1) (Paris: Masson, 1988).Google Scholar
13Lions, J. L. and Magènes, E.. Problèmes aux Limites Non Homogénes et Applications, (Vols I, II) (Paris: Dunod, 1968).Google Scholar
14Montoro, L. Marco, Carracedo, C. Martínez and Alix, M. Sanz. Fractional powers of operators. J. Math. Soc. Japan, 40 (1988), 331–47.Google Scholar
15Carracedo, C. Martinez and Sanz, M.Alix. Fractional powers of non-densely defined operators. Ann., Scuola Norm. Sup. Pisa Cl. Sci., 18 (1991), 443–54.Google Scholar
16Palencia, C. and Alonso-Mallo, I.. Abstract initial boundary values problems. Proc. Roy. Soc., Edinburgh Sect. A, 124A (1994), 879–908.CrossRefGoogle Scholar
17Pazy, A.. Semigroups of Linear Operators and Applications to Partial Differential Equations, (Berlin: Springer, 1983).Google Scholar
18Rauch, J.. L2 is a continuable initial condition for Kreiss' problem. Comm. Pure Appl. Math., 25 (1972), 265–85.CrossRefGoogle Scholar
19Rudin, W.. Real and Complex Analysis, 2nd edn (New York: McGraw-Hill, 1974).Google Scholar
20Schwartz, J.. A remark on inequalities of Calderon–Zygmund type for vector-valued functions. Comm., Pure Appl. Math., 14 (1961), 785–99.CrossRefGoogle Scholar
21Sinestrari, E.. On the abstract Cauchy problem of parabolic type in spaces of continuous functions. J. Math. Anal. Appl., 107 (1985), 16–66.Google Scholar
22Triebel, H.. Interpolation Theory, Function Spaces, Differential Operators, (Amsterdam: North-Holland, 1978).Google Scholar
23Weiss, G.. Admissible observations operators for linear semigroups. Israel J. Math., 65 (1989), 17–43.CrossRefGoogle Scholar