Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-27T09:43:09.916Z Has data issue: false hasContentIssue false
  • English
  • Français

On pathological properties of fixed point algebras in Kirchberg algebras

Part of: Selfadjoint operator algebras Locally compact groups and their algebras

Published online by Cambridge University Press:  20 September 2019

Yuhei Suzuki
Yuhei Suzuki*
Affiliation:
Graduate school of mathematics, Nagoya University, Chikusaku, Nagoya, 464-8602, Japan ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate how the fixed point algebra of a C*-dynamical system can differ from the underlying C*-algebra. For any exact group Γ and any infinite group Λ, we construct an outer action of Λ on the Cuntz algebra 𝒪2 whose fixed point algebra is almost equal to the reduced group C*-algebra 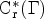${\rm C}_{\rm r}^* (\Gamma)$. Moreover, we show that every infinite group admits outer actions on all Kirchberg algebras whose fixed point algebras fail the completely bounded approximation property.

Keywords

Fixed point algebrasnuclearitynon-commutative dynamical systems

MSC classification

Primary: 22D25: $C^*$-algebras and $W^*$-algebras in relation to group representations 46L55: Noncommutative dynamical systems
Secondary: 46L05: General theory of $C^*$-algebras
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 150 , Issue 6 , December 2020 , pp. 3087 - 3096
Check for updates
Copyright
Copyright © 2019 The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Blackadar, B.. K-Theory for Operator Algebras, 2nd edn, vol. 5 (Berkeley, CA: Mathematical Sciences Research Institute Publications, 1998).Google Scholar
2Brown, N. P. and Ozawa, N.. C*-Algebras and Finite-Dimensional Approximations.Graduate Studies in Mathematics, vol. 88 (Providence, RI: American Mathematical Society, 2008).Google Scholar
3Connes, A.. Classification of injective factors. Cases II1, II∞, IIIλ, λ ≠ 1. Ann. Math. (2) 104 (1976), 73–115.CrossRefGoogle Scholar
4Cuntz, J.. Simple C*-algebras generated by isometries. Comm. Math. Phys. 57 (1977), 173–185.CrossRefGoogle Scholar
5Cuntz, J.. Dimension functions on simple C*-algebras. Math. Ann. 233 (1978), 145–153.CrossRefGoogle Scholar
6Cuntz, J.. K-theory for certain C*-algebras. Ann. Math. 113 (1981), 181–197.CrossRefGoogle Scholar
7Futamura, H., Kataoka, N. and Kishimoto, A.. Homogeneity of the pure state space for separable C*-algebras. Int. J. Math. 12 (2001), 813–845.Google Scholar
8Haagerup, U.. Quasitraces on exact C*-algebras are traces. C. R. Math. Acad. Sci. Soc. R. Can. 36 (2014), 67–92.Google Scholar
9Haagerup, U. and Kraus, J.. Approximation properties for group C*-algebras and group von Neumann algebras. Trans. Amer. Math. Soc. 344 (1994), 667–699.Google Scholar
10Izumi, M.. Inclusions of simple C*-algebras. J. Reine Angew. Math. 547 (2002), 97–138.Google Scholar
11Izumi, M.. Finite group actions on C*-algebras with the Rohlin property I. Duke Math. J. 122 (2004), 233–280.CrossRefGoogle Scholar
12Izumi, M. and Matui, H.. Poly-ℤ group actions on Kirchberg algebras I. To appear in Int. Math. Res. Not., arXiv:1810.05850.Google Scholar
13Izumi, M. and Matui, H.. Poly-ℤ group actions on Kirchberg algebras II. Preprint, arXiv:1906.03818.Google Scholar
14Kasparov, G.. Equivariant K K-theory and the Novikov conjecture. Invent. Math. 91 (1988), 147–201.Google Scholar
15Kirchberg, E.. Commutants of unitaries in UHF-algebras and functorial properties of exactness. J. Reine Angew. Math. 452 (1994), 39–77.Google Scholar
16Kirchberg, E.. The classification of purely infinite C*-algebras using Kasparov's theory. Preprint.Google Scholar
17Kirchberg, E. and Phillips, N. C.. Embedding of exact C*-algebras in the Cuntz algebra 𝒪2. J. Reine Angew. Math. 525 (2000), 17–53.CrossRefGoogle Scholar
18Kishimoto, A.. Outer automorphisms and reduced crossed products of simple C*-algebras. Comm. Math. Phys. 81 (1981), 429–435.CrossRefGoogle Scholar
19Kishimoto, A., Ozawa, N. and Sakai, S.. Homogeneity of the pure state space of a separable C*-algebra. Canad. Math. Bull. 46 (2003), 365–372.CrossRefGoogle Scholar
20Lafforgue, V. and de la Salle, M.. Noncommutative L p-spaces without the completely bounded approximation property. Duke Math. J. 160 (2011), 71–116.Google Scholar
21Nakamura, H.. Aperiodic automorphisms of nuclear purely infinite simple C*-algebras. Ergodic Theory Dyn. Syst. 20 (2000), 1749–1765.CrossRefGoogle Scholar
22Neumann, B. H.. Groups covered by permutable subsets. J. London Math. Soc. 29 (1954), 236–248.Google Scholar
23Olesen, D. and Pedersen, G. K.. Applications of the Connes spectrum to C*-dynamical systems III. J. Funct. Anal. 45 (1981), 357–390.CrossRefGoogle Scholar
24Ozawa, N.. There is no separable universal II1-factor. Proc. Amer. Math. Soc. 132 (2004), 487–490.CrossRefGoogle Scholar
25Ozawa, N.. Weak amenability of hyperbolic groups. Groups Geom. Dyn. 2 (2008), 271–280.CrossRefGoogle Scholar
26Ozawa, N.. Examples of groups which are not weakly amenable. Kyoto J. Math. 52 (2012), 333–344.CrossRefGoogle Scholar
27Phillips, N. C.. A classification theorem for nuclear purely infinite simple C*-algebras. Doc. Math. 5 (2000), 49–114.Google Scholar
28Pimsner, M. and Voiculescu, D.. K-groups of reduced crossed products by free groups. J. Operator Theory 8 (1982), 131–156.Google Scholar
29Rørdam, M.. Classification of Nuclear, Simple C*-Algebras. Vol. 126 of Encyclopaedia Math. Sci.,pp. 1–145 (Berlin: Springer, 2002).Google Scholar
30Rosenberg, J. and Schochet, C.. The Künneth theorem and the universal coefficient theorem for Kasparov's generalized K-functor. Duke Math. J. 55 (1987), 431–474.Google Scholar
31Suzuki, Y.. Group C*-algebras as decreasing intersection of nuclear C*-algebras. Amer. J. Math. 139 (2017), 681–705.Google Scholar
32Suzuki, Y.. Simple equivariant C*-algebras whose full and reduced crossed products coincide. To appear in J. Noncommut. Geom., arXiv:1801.06949.Google Scholar
33Suzuki, Y.. Complete descriptions of intermediate operator algebras by intermediate extensions of dynamical systems. To appear in Comm. Math. Phys., arXiv:1805.02077.Google Scholar
34Suzuki, Y.. Rigid sides of approximately finite dimensional simple operator algebras in non-separable category. To appear in Int. Math. Res. Not., arXiv:1809.08810.Google Scholar
35Szabó, G.. Equivariant Kirchberg-Phillips-type absorption for amenable group actions. Comm. Math. Phys. 361 (2018), 1115–1154.CrossRefGoogle Scholar
36Watatani, Y.. Index for C*-subalgebras. Mem. Amer. Math. Soc. 424 (1990).Google Scholar