Hostname: page-component-745bb68f8f-mzp66 Total loading time: 0 Render date: 2025-01-12T12:55:06.107Z Has data issue: false hasContentIssue false
  • English
  • Français

On multiple solutions for Berman's problem

Published online by Cambridge University Press:  14 November 2011

Tzy-Wei Hwang  and
Ching-An Wang
Tzy-Wei Hwang
Affiliation:
Department of Mathematics, National Kaohsiung Normal University, Kaohsiung, Taiwan 80264
Ching-An Wang
Affiliation:
Institute of Applied Mathematics, National Chung Cheng University, Minghsiung, Taiwan 62117
Get access Rights & Permissions [Opens in a new window]

Synopsis

We study Berman's problem

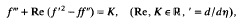
subjects to the conditions f(0) =f″(0) = f′(1) = f(1)− 1 = 0, which arises from the study of laminar flows in channels with porous walls. Positive (negative) Re denotes the case of suction (injection) flows. Preliminary numerical studies indicated the existence of three different types of solutions and a small portion of mathematical evidence was provided. In this paper, we are able to show that there exist connected sets in the Re-K plane on which different types of solutions occur. In particular, our result verifies that the problem possesses all three types of suction solutions for sufficiently large Re. Moreover, the limiting injection solution is also obtained.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 121 , Issue 3-4 , 1992 , pp. 219 - 230
Copyright
Copyright © Royal Society of Edinburgh 1992

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Berman, A. S.. Laminar flow in channels with porous walls. J. Appl. Phys. 24 (1953), 1232–1235.CrossRefGoogle Scholar
2Berman, A. S.. Effects of porous boundaries on the flow of fluids in systems of various geometries. Proc. Second United Nations International Conference on the Peaceful Uses of Atomic Energy, Vol. 4, pp. 351–358 (Geneva: United Nations, 1958).Google Scholar
3Raithby, G.. Laminar heat transfer in the thermal entrance region of circular tubes and two-dimensional rectangular ducts with wall suction and injection. Internal. J. Heat and Mass Transfer 14 (1971), 223–243.CrossRefGoogle Scholar
4Robinson, W. A.. The existence of multiple solutions for the laminar flow in a uniformly porous channel with suction at both walls. J. Engrg. Math. 10 (1976), 23–40.CrossRefGoogle Scholar
5Skalak, F. M. and Wang, C. Y.. On the nonunique solutions of laminar flow through a porous tube or channel. SIAM J. Appl. Math. 34 (1978), 535–544.CrossRefGoogle Scholar
6Shih, K. E.. On the existence of solutions of an equation arising in the theory of laminar flow in a uniformly porous channel with injection. SIAM J. Appl. Math. 47 (1987), 526–533.CrossRefGoogle Scholar
7Wang, C. A., Hwang, T. W. and Chen, Y. Y.. Existence of solutions of Berman's equation from laminar flows in a porous channel with suction. Comput. Math. Appl. 20 (1990), 35–40.CrossRefGoogle Scholar
8Hastings, S. P., Lu, C. and MacGillivary, A. D.. A boundary value problem with multiple solutions from the theory of laminar flow (preprint).Google Scholar
9Yuan, S. W. and Finkelstein, A. B.. Laminar pipe flow with injection and suction through a porous wall. Trans. ASME Ser. E J. Appl. Mech. 78 (1956), 719–724.Google Scholar