Hostname: page-component-f554764f5-nwwvg Total loading time: 0 Render date: 2025-04-15T08:50:34.045Z Has data issue: false hasContentIssue false
  • English
  • Français

On mixed local–nonlocal problems with Hardy potential

Part of: Equations and systems of special type Elliptic equations and systems Partial differential equations

Published online by Cambridge University Press:  11 April 2025

Stefano Biagi Open the ORCID record for Stefano Biagi [Opens in a new window] ,
Francesco Esposito Open the ORCID record for Francesco Esposito [Opens in a new window] ,
Luigi Montoro  and
Eugenio Vecchi Open the ORCID record for Eugenio Vecchi [Opens in a new window]
Stefano Biagi
Affiliation:
Dipartimento di Matematica, Politecnico di Milano, Via Bonardi 9, 20133, Milano, Italy ([email protected])
Francesco Esposito
Affiliation:
Dipartimento di Matematica e Informatica, Università della Calabria, Via Pietro Bucci Cubo 31B, 87036, Arcavacata di Rende, Cosenza, Italy ([email protected]) (corresponding author)
Luigi Montoro
Affiliation:
Dipartimento di Matematica e Informatica, Università della Calabria, Via Pietro Bucci Cubo 31B, 87036, Arcavacata di Rende, Cosenza, Italy ([email protected])
Eugenio Vecchi
Affiliation:
Dipartimento di Matematica, Università di Bologna, Piazza di Porta San Donato 5, 40126, Bologna, Italy ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

In this article, we study the effect of the Hardy potential on existence, uniqueness, and optimal summability of solutions of the mixed local–nonlocal elliptic problem

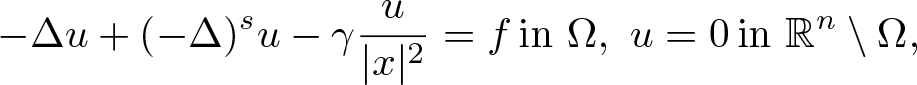\begin{equation*}-\Delta u + (-\Delta)^s u - \gamma \frac{u}{|x|^2}=f \,\text{in } \Omega, \ u=0 \,\text{in } {\mathbb R}^n \setminus \Omega,\end{equation*}
where Ω is a bounded domain in ${\mathbb R}^n$ containing the origin and γ > 0. In particular, we will discuss the existence, non-existence, and uniqueness of solutions in terms of the summability of f and of the value of the parameter γ.

Keywords

existence and regularity of solutionsHardy potentialmixed local–nonlocal PDEshardy inequaltiesSOLA solutions

MSC classification

Primary: 35J75: Singular elliptic equations 35A01: Existence problems 35B65: Smoothness and regularity of solutions
Secondary: 35M10: Equations of mixed type 35J15: Second-order elliptic equations
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , First View , pp. 1 - 34
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Abdellaoui, B., Medina, M., Peral, I. and Primo, A.. The effect of the Hardy potential in some Calderón-Zygmund properties for the fractional Laplacian. J. Differential Equations 260 (2016), 8160–8206.CrossRefGoogle Scholar
Abdellaoui, B. and Peral, I.. A note on a critical problem with natural growth in the gradient. J. Eur. Math. Soc. (JEMS) 8 (2006), 157–170.CrossRefGoogle Scholar
Antonini, C. A. and Cozzi, M.. Global gradient regularity and a Hopf lemma for quasilinear operators of mixed local-nonlocal type. J. Differential Equations 425 (2025), 342–382.CrossRefGoogle Scholar
Arora, R., Nguyen, P.T. and Radulescu, V., A large class of nonlocal elliptic equations with singular nonlinearities, preprint. https://arxiv.org/abs/2211.06634.Google Scholar
Arora, R. and Radulescu, V.. Combined effects in mixed local-nonlocal stationary problems, Proceedings of the Royal Society of Edinburgh: Section A Mathematics, , Published online 2023. doi:10.1017/prm.2023.801.06701.CrossRefGoogle Scholar
Biagi, S., Dipierro, S., Valdinoci, E. and Vecchi, E.. Mixed local and nonlocal elliptic operators: Regularity and maximum principles. Comm. Partial Differential Equations 47 (2022), 585–629.CrossRefGoogle Scholar
Biagi, S., Dipierro, S., Valdinoci, E. and Vecchi, E.. A Faber-Krahn inequality for mixed local and nonlocal operators. J. Anal. Math. 150 (2023), 405–448.CrossRefGoogle Scholar
Biagi, S., Mugnai, D. and Vecchi, E.. A Brezis–Oswald approach for mixed local and nonlocal operators. Commun. Contemp. Math. 26 (2024), 2250057.CrossRefGoogle Scholar
Biagi, S. and Vecchi, E.. Multiplicity of positive solutions for mixed local-nonlocal singular critical problems. Calc. Var. Partial Differ. Equ. 63 (2024), 221.CrossRefGoogle Scholar
Boccardo, L., Orsina, L. and Peral, I.. A remark on existence and optimal summability of solutions of elliptic problems involving Hardy potential. Discrete Contin. Dyn. Syst. 16 (2006), 513–523.CrossRefGoogle Scholar
Bony, J.-M., Courrège, P. and Priouret, P.. Semi-groupes de Feller sur une variété à bord compacte et problèmes aux limites intégro-différentiels du second ordre donnant lieu au principe du maximum. Ann. Inst. Fourier (Grenoble) 18 (1968), 369–521.CrossRefGoogle Scholar
Cancelier, C.. Problèmes aux limites pseudo-différentiels donnant lieu au principe du maximum. Comm. Partial Differential Equations 11 (1986), 1677–1726.CrossRefGoogle Scholar
Chen, Z.-Q., Kim, P., Song, R. and Vondraček, Z.. Boundary Harnack principle for $\Delta + \Delta^{\unicode{x03B1}/2}$. Trans. Amer. Math. Soc. 364 (2012), 4169–4205.CrossRefGoogle Scholar
De Filippis, C. and Mingione, G.. Gradient regularity in mixed local and nonlocal problems. Math. Ann. 388 (2024), 261–328.CrossRefGoogle Scholar
Di Nezza, E., Palatucci, G. and Valdinoci, E.. Hitchhiker’s guide to the fractional Sobolev spaces. Bull. Sci. Math. 136 (2012), 521–573.CrossRefGoogle Scholar
Dipierro, S., Proietti Lippi, E. and Valdinoci, E.. (Non)local logistic equations with Neumann conditions. Ann. Inst. H. Poincaré C Anal. Non Linéaire. 40 (2022), 1093–1166. doi:10.4171/AIHPC/57.CrossRefGoogle Scholar
Fall, M. M. and Musina, R.. Sharp nonexistence results for a linear elliptic inequality involving Hardy and Leray potentials. J. Inequal. Appl. 2011, 917201.CrossRefGoogle Scholar
Garain, P.. On a class of mixed local and nonlocal semilinear elliptic equation with singular nonlinearity. J. Geom. Anal. 33 (2023), 212.CrossRefGoogle Scholar
Garain, P. and Kinnunen, J.. On the regularity theory for mixed local and nonlocal quasilinear elliptic equations. Trans. Amer. Math. Soc. 375 (2022), 5393–5423.CrossRefGoogle Scholar
Garain, P. and Lindgren, E.. Higher Hölder regularity for mixed local and nonlocal degenerate elliptic equations. Calc. Var. 62 (2023), 67.CrossRefGoogle Scholar
Hardy, G. H., Littlewood, J. E. and Polya, G.. Inequalities. Reprint of the 1952 edition (Cambridge Mathematical Library, Cambridge University Press, Cambridge, 1988).Google Scholar
Leonori, T., Peral, I., Primo, A. and Soria, F.. Basic estimates for solutions of a class of nonlocal elliptic and parabolic equations. Discrete Contin. Dyn. Syst. 35 (2015), 6031–6068.CrossRefGoogle Scholar
Peral, I. and Soria, F.. Elliptic and parabolic equations involving the Hardy-Leray potential, De Gruyter Series in Nonlinear Analysis and Applications, Vol. 38 (Walter de Gruyter GmbH, Berlin/Boston, 2021).Google Scholar
Biagi, S., Dipierro, S., Valdinoci, E. and Vecchi, E., A Brezis-Nirenberg type result for mixed local and nonlocal operators, preprint. https://arxiv.org/abs/2209.07502.Google Scholar
Stampacchia, G.. Le problème de Dirichlet pour les équations elliptiques du second ordre à coefficients discontinus. Ann. Inst. Fourier (Grenoble) 15 (1965), 189–258.CrossRefGoogle Scholar
Su, X., Valdinoci, E., Wei, Y. and Zhang, J.. Regularity results for solutions of mixed local and nonlocal elliptic equations. Math. Z. 302 (2022), 1855–1878.CrossRefGoogle Scholar
Su, X., Valdinoci, E., Wei, Y. and Zhang, J.. On some regularity properties of mixed local and nonlocal elliptic equations. J. Differential Equations 416 (2025), 576–613.CrossRefGoogle Scholar
Vazquez, J. L. and Zuazua, E.. The Hardy inequality and the asymptotic behaviour of the heat equation with an inverse-square potential. J. Funct. Anal. 173 (2000), 103–153.CrossRefGoogle Scholar