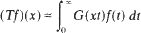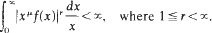Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Heywood, P.
and
Rooney, P.G.
1988.
On the inversion of the even and odd Hilbert transformations.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 109,
Issue. 3-4,
p.
201.
Heywood, P.
and
Rooney, P. G.
1990.
On the Gegenbauer transformation.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 115,
Issue. 1-2,
p.
151.
McBride, A. C.
and
Spratt, W. J.
1991.
On the Range and Invertibility of a Class of Melon Multiplier Transforms III.
Canadian Journal of Mathematics,
Vol. 43,
Issue. 6,
p.
1323.
Kilbas, Anatoly A.
Saigo, Megumi
and
Shlapakov, Sergei A.
1993.
Integral transforms with fox'sH-function in spaces of summable functions.
Integral Transforms and Special Functions,
Vol. 1,
Issue. 2,
p.
87.
Glaeske, Hans-Jürgen
and
Kilbas, Anatoly A.
1998.
Bessel-type Integral Transforms on % MathType!MTEF!2!1!+-% feaaeaart1ev0aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn% hiov2DGi1BTfMBaeXanrfitLxBI9gBaerbd9wDYLwzYbItLDharqqt% ubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq% -Jc9vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0x% fr-xfr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyuam% aaBaaaleaacaaIXaGaaGimaaqabaGccqGH9aqpciGGSbGaaiOBaiaa% ysW7caWGRbWaaSbaaSqaaiaadsfacaaIXaaabeaakiaac+cacaWGRb% WaaSbaaSqaaiaadsfacaaIYaaabeaakiabg2da9iabgkHiTmaabmaa% baGaamyramaaBaaaleaacaWGHbaabeaakiaac+cacaWGsbaacaGLOa% GaayzkaaGaey41aq7aaiWaaeaadaqadaqaaiaadsfadaWgaaWcbaGa% aGOmaaqabaGccqGHsislcaWGubWaaSbaaSqaaiaaigdaaeqaaaGcca% GLOaGaayzkaaGaai4laiaacIcacaWGubWaaSbaaSqaaiaaikdaaeqa% aOGaaGjbVlaadsfadaWgaaWcbaGaamysaaqabaGccaGGPaaacaGL7b% GaayzFaaaaaa!5C4A! ${\cal L}_{\nu,r}$ ⋌e-spaces.
Results in Mathematics,
Vol. 34,
Issue. 3-4,
p.
320.
Yarotskaya, L.D.
2000.
On index transforms with meijer'sG-function kernels.
Integral Transforms and Special Functions,
Vol. 10,
Issue. 3-4,
p.
309.
Kilbas, A.A.
and
Borovco, A.N.
2000.
Hardy-Titchmarsh And Hankel Type Transforms In -Spaces.
Integral Transforms and Special Functions,
Vol. 10,
Issue. 3-4,
p.
239.
Kilbas, A.A.
Saigo, M.
and
Trujillo, J.J.
2000.
On The Meijer Transform In Space.
Integral Transforms and Special Functions,
Vol. 10,
Issue. 3-4,
p.
267.
A.Kilbas, Anatoly
and
Trujillo, Juan J.
2000.
Generalized hankel transform no space.
Integral Transforms and Special Functions,
Vol. 9,
Issue. 4,
p.
271.
Glaeske, H.-J.
Kilbas, Anatoly A.
and
Saigo, Megumi
2000.
A modified Bessel-type integral transform and its compositions with fractional calculus operators on spaces Fp,μ and Fp,μ′.
Journal of Computational and Applied Mathematics,
Vol. 118,
Issue. 1-2,
p.
151.
Butzer, Paul L.
Kilbas, Anatoly A.
and
Trujillo, Juan J.
2002.
Fractional calculus in the Mellin setting and Hadamard-type fractional integrals.
Journal of Mathematical Analysis and Applications,
Vol. 269,
Issue. 1,
p.
1.
Glaeske, Hans–Jürgen
and
Kilbas, Anatoly A.
2003.
A generalized Hankel transform on Lν,r–spaces.
Mathematische Nachrichten,
Vol. 258,
Issue. 1,
p.
16.
Yarotskaya, L. D.
2005.
On the inversion of someW-transform.
Integral Transforms and Special Functions,
Vol. 16,
Issue. 5-6,
p.
505.
Naik, Shanoja
and
Haubold, Hans
2016.
On the q-Laplace Transform and Related Special Functions.
Axioms,
Vol. 5,
Issue. 3,
p.
24.
Kiryakova, Virginia
2021.
A Guide to Special Functions in Fractional Calculus.
Mathematics,
Vol. 9,
Issue. 1,
p.
106.
Sitnik, S. M.
Skoromnik, O. V.
and
Shlapakov, S. A.
2022.
Multi-Dimensional Generalized Integral Transform in the Weighted Spaces of Summable Functions.
Lobachevskii Journal of Mathematics,
Vol. 43,
Issue. 6,
p.
1408.
El-Metwally, H.
Masood, F. M.
Abu-Gdairi, Radwan
and
Al-shami, Tareq M.
2023.
Mathematics and Computation.
Vol. 418,
Issue. ,
p.
437.
SITNIK, S.
SKOROMNIK, O.
and
PAPKOVICH, M.
2023.
TWO-DIMENSIONAL INTEGRAL H-TRANSFORM
IN WEIGHTED SPACES OF SUMMABLE FUNCTIONS.
HERALD OF POLOTSK STATE UNIVERSITY. Series С FUNDAMENTAL SCIENCES,
p.
93.
Sitnik, S. M.
Skoromnik, O. V.
and
Papkopvich, M. V.
2023.
Differential Equations, Mathematical Modeling and Computational Algorithms.
Vol. 423,
Issue. ,
p.
193.
SITNIK, S.
SKOROMNIK, O.
and
KUROKHTINA, A.
2024.
INTEGRAL TRANSFORMATION WITH THE MITTAG–LEFFLER FUNCTION
IN SPACES OF LEBESGUE-MEASURABLE FUNCTIONS.
HERALD OF POLOTSK STATE UNIVERSITY. Series С FUNDAMENTAL SCIENCES,
p.
67.