On higher differentiability of solutions of parabolic systems with discontinuous coefficients and (p, q)-growth

Abstract

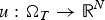We consider weak solutions $u:\Omega _T\to {\open R}^N$ to parabolic systems of the type

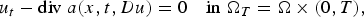$$u_t-{\rm div}\;a(x,t,Du) = 0\quad {\rm in}\;\Omega _T = \Omega \times (0,T),$$

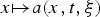where the function a(x, t, ξ) satisfies (p, q)-growth conditions. We give an a priori estimate for weak solutions in the case of possibly discontinuous coefficients. More precisely, the partial maps $x\mapsto a(x,t,\xi )$ under consideration may not be continuous, but may only possess a Sobolev-type regularity. In a certain sense, our assumption means that the weak derivatives 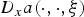$D_xa(\cdot ,\cdot ,\xi )$ are contained in the class 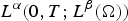$L^\alpha (0,T;L^\beta (\Omega ))$, where the integrability exponents 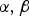$\alpha ,\beta $ are coupled by

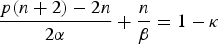$$\displaystyle{{p(n + 2)-2n} \over {2\alpha }} + \displaystyle{n \over \beta } = 1-\kappa $$

for some κ ∈ (0,1). For the gap between the two growth exponents we assume

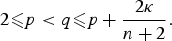$$2 \les p < q \les p + \displaystyle{{2\kappa } \over {n + 2}}.$$

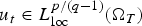Under further assumptions on the integrability of the spatial gradient, we prove a result on higher differentiability in space as well as the existence of a weak time derivative $u_t\in L^{p/(q-1)}_{{\rm loc}}(\Omega _T)$. We use the corresponding a priori estimate to deduce the existence of solutions of Cauchy–Dirichlet problems with the mentioned higher differentiability property.