Hostname: page-component-669899f699-2mbcq Total loading time: 0 Render date: 2025-04-25T09:42:26.157Z Has data issue: false hasContentIssue false
  • English
  • Français

On a perturbed critical semilinear equation with singularity

Part of: Equations and inequalities involving nonlinear operators Elliptic equations and systems

Published online by Cambridge University Press:  27 February 2025

Sarika Goyal  and
Kunnath Sandeep
Sarika Goyal
Affiliation:
Department of Mathematics, Netaji Subhas university of Technology, Dwarka, Delhi, India ([email protected])
Kunnath Sandeep*
Affiliation:
TIFR Centre for Applicable Mathematics, Post Bag No. 6503, Sharadanagar, Yelahanka New Town, Bangalore, India ([email protected]) (corresponding author)
*
*Corresponding author.
Get access Rights & Permissions [Opens in a new window]

Abstract

In this article, we investigate necessary and sufficient conditions on the perturbation ρ for the existence of positive least energy solutions of the critical singular semilinear elliptic equation 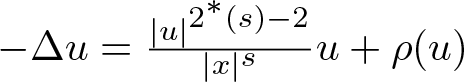$ -\Delta u = \frac{|u|^{2^{*}(s)-2}}{|x|^s}u + \rho(u) $ with Dirichlet boundary condition in a bounded smooth domain in 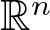$\mathbb R^n$ containing the origin, where 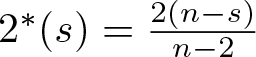$2^*(s)=\frac{2(n-s)}{n-2}$, 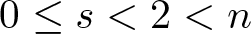$0\leq s \lt 2 \lt n$. We show that the almost necessary and sufficient condition obtained for the case s = 0 in [1] differs conceptually when 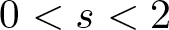$0 \lt s \lt 2$.

Keywords

blow-up analysiscritical growthlack of compactnessleast energy solutionSobolev–Hardy inequality

MSC classification

Primary: 35J60: Nonlinear elliptic equations
Secondary: 35J75: Singular elliptic equations 47J30: Variational methods
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , First View , pp. 1 - 35
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Adimurthi, G. M. and Sandeep, K.. A sharp solvability condition in higher dimensions for some Brezis-Nirenberg type equation. Calc. Var. Partial Differ. Equ. 14 (2002), 275–317.Google Scholar
Brézis, H. and Nirenberg, L.. Positive solutions of nonlinear elliptic equations involving critical Sobolev exponents. Comm. Pure Appl. Math. 36 (1983), 437–477.CrossRefGoogle Scholar
Chou, K. S. and Chu, C. W.. On the best constant for a weighted Sobolev-Hardy inequality. J. London Math. Soc. (2) 48 (1993), 137–151.CrossRefGoogle Scholar
Druet, O.. Elliptic equations with critical Sobolev exponents in dimension 3. Ann. Inst. H. Poincaré C Anal. Non Linéaire 19 (2002), 125–142.CrossRefGoogle Scholar
Dutta, R.. Apriori decay estimates for Hardy-Sobolev-Maz’ya equations. Calc. Var. Partial Differ. Equ. 61 (2022), .CrossRefGoogle Scholar
Ghoussoub, N. and Kang, X. S.. Hardy-Sobolev critical elliptic equations with boundary singularities. Ann. Inst. H. Poincaré C Anal. Non Linéaire 21 (2004), 767–793.CrossRefGoogle Scholar
Ghoussoub, N. and Robert, F.. The Hardy-Schrödinger operator with interior singularity: the remaining cases. Calc. Var. Partial Differ. Equ. 56 (2017), , .CrossRefGoogle Scholar
Ghoussoub, N. and Yuan, C.. Multiple solutions for quasi-linear PDEs involving the critical Sobolev and Hardy exponents. Trans. Amer. Math. Soc. 352 (2000), 5703–5743.CrossRefGoogle Scholar
Gidas, B., Ni, W. M. and Nirenberg, L.. Symmetry and related properties via the maximum principle. Comm. Math. Phys. 68 (1979), 209–243.CrossRefGoogle Scholar
Han, Q. and Lin, F.. Elliptic partial differential equations, Courant Lecture Notes in Mathematics, 2nd edn., Vol. 1 (Courant Institute of Mathematical Sciences, New York; American Mathematical Society, Providence, RI, 2011).Google Scholar
Mancini, G., Fabbri, I. and Sandeep, K.. Classification of solutions of a critical Hardy-Sobolev operator. J. Differ. Equ. 224 (2006), 258–276.CrossRefGoogle Scholar
Robert, F. and Sandeep, K.. Sharp solvability conditions for a fourth-order equation with perturbation. Differ. Int. Equ. 16 (2003), 1181–1214.Google Scholar
Schoen, R.. Conformal deformation of a Riemannian metric to constant scalar curvature. J. Differ. Geom. 20 (1984), 479–495.CrossRefGoogle Scholar
Smets, D. and Willem, M.. Partial symmetry and asymptotic behavior for some elliptic variational problems. Calc. Var. Partial Differ. Equ. 18 (2003), 57–75.CrossRefGoogle Scholar
Terracini, S.. On positive entire solutions to a class of equations with a singular coefficient and critical exponent. Adv. Differ. Equ. 1 (1996), 241–264.Google Scholar