Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-23T21:41:33.314Z Has data issue: false hasContentIssue false
  • English
  • Français

On a class of interpolation series

Published online by Cambridge University Press:  14 November 2011

Einar Hille
Einar Hille
Affiliation:
La Jolla, California 92037, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Synopsis

This paper deals with a class of interpolation series of the form

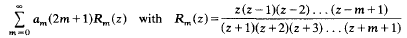
called R-series. It is equiconvergent with the Dirichlet series

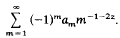
If the nth Legendre polynomial for the interval (0,1) is denoted by (−1)nLn(t), then the bilinear formula

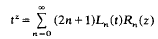
serves as generating function for the Rn(z). It also leads in easy steps to R-series expansions for rational functions.

Lagrange [7] has shown that a function holomorphic and of finite rate of growth in a right half-plane can be expanded in an R-series whose abscissa of convergence is limited by the rate of growth of f(z). The converse problem is attacked in Theorem 2 below where it is shown that

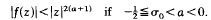
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 84 , Issue 3-4 , 1979 , pp. 283 - 307
Copyright
Copyright © Royal Society of Edinburgh 1979

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Hausdorff, F.. Momentprobleme für ein endliches Intervall. Math. Z. 16 (1923), 220–248.CrossRefGoogle Scholar
2Hermite, Ch. and Stieltjes, T. J.. Correspondence d'Hermite et de Stieltjes (Paris: Gauthier-Villars, 1892).Google Scholar
3Hille, E.. Analytic function Theory, Vols I and II (Boston: Ginn, 1959 and 1962: Chelsea reprints, 1974).Google Scholar
4Hille, E.. Bilinear formulas in the theory of the transformation of Laplace. Compositio Math. 6 (1938), 93–102.Google Scholar
5Hille, E.. Classical Analysis and Functional Analysis. Selected Papers, edited by Kallman, Robert R. (Edinburgh, Mass.: M.I.T. Press, 1975).Google Scholar
6Hille, E. and Tamarkin, J. D.. A remark on Fourier transforms and functions analytic in a half-plane. Compositio Math. 1 (1934), 98–102.Google Scholar
7Lagrange, R.. Mémoire sur les séries d'interpolation. Acta Math. 64 (1934), 1–80.CrossRefGoogle Scholar
8Riesz, F.. Uber eine Verallgemeinerung der Parsevalschen Formel. Math. Z. 18 (1923), 117–124.CrossRefGoogle Scholar
9Shohat, J. A. and Tamarkin, J. D.. The problem of moments. Math. Surveys I (New York: Amer. Math. Soc, 1943).Google Scholar
10Szegö, G.. Orthogonal polynomials. Amer. Math. Soc. Coll. Publ. 23 (New York: A.M.S., 1939).Google Scholar