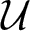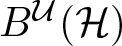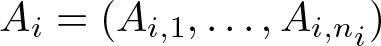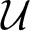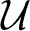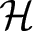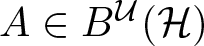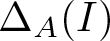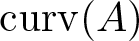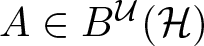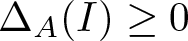1. Introduction
In 2000, Arveson [Reference Arveson2] introduced and studied the curvature and Euler characteristic for finite rank contractive Hilbert modules over ![]() ${\mathbb C}[z_1,\dots, z_n]$, which are in fact numerical invariants for the commuting n-tuples of operators
${\mathbb C}[z_1,\dots, z_n]$, which are in fact numerical invariants for the commuting n-tuples of operators ![]() $X:=(X_1,\ldots, X_n)\in B({\mathcal H})^n$, with
$X:=(X_1,\ldots, X_n)\in B({\mathcal H})^n$, with ![]() $\Delta_X:=I-X_1X_1^*-\cdots -X_nX_n^*\geq 0$ and rank
$\Delta_X:=I-X_1X_1^*-\cdots -X_nX_n^*\geq 0$ and rank ![]() $\Delta_X \lt \infty$, where
$\Delta_X \lt \infty$, where ![]() $B({\mathcal H})$ is the algebra of bounded linear operators on a Hilbert space
$B({\mathcal H})$ is the algebra of bounded linear operators on a Hilbert space ![]() ${\mathcal H}$. Shortly after, the author [Reference Popescu20] and, independently, Kribs [Reference Kribs14] defined and studied a notion of curvature for the elements in the noncommutative unit ball
${\mathcal H}$. Shortly after, the author [Reference Popescu20] and, independently, Kribs [Reference Kribs14] defined and studied a notion of curvature for the elements in the noncommutative unit ball
and, as a consequence, for the invariant subspaces under the left creation operators ![]() $S_1,\ldots, S_n$ on the full Fock space
$S_1,\ldots, S_n$ on the full Fock space ![]() $F^2(H_n)$ with n generators. Some of these results were extended by Muhly and Solel [Reference Muhly and Solel16] to a class of completely positive maps on semifinite factors. The theory of Arveson’s curvature on the symmetric Fock space
$F^2(H_n)$ with n generators. Some of these results were extended by Muhly and Solel [Reference Muhly and Solel16] to a class of completely positive maps on semifinite factors. The theory of Arveson’s curvature on the symmetric Fock space ![]() $F_s^2(H_n)$ with n generators was significantly expanded due to the work by Greene, Richter, and Sundberg [Reference Greene, Richter and Sundberg11]; Fang [Reference Fang7]; and Gleason, Richter, and Sundberg [Reference Gleason, Richter and Sundberg10]. Engliš remarked in [Reference Englis6] that using Arveson’s ideas, one can extend the notion of curvature to complete Nevanlinna–Pick kernels. The extension of Arveson’s theory to holomorphic spaces with non-Nevanlinna–Pick kernels was first considered by Fang [Reference Fang9] who was able to show that the main results about the curvature invariant on the symmetric Fock space carry over to the Hardy space
$F_s^2(H_n)$ with n generators was significantly expanded due to the work by Greene, Richter, and Sundberg [Reference Greene, Richter and Sundberg11]; Fang [Reference Fang7]; and Gleason, Richter, and Sundberg [Reference Gleason, Richter and Sundberg10]. Engliš remarked in [Reference Englis6] that using Arveson’s ideas, one can extend the notion of curvature to complete Nevanlinna–Pick kernels. The extension of Arveson’s theory to holomorphic spaces with non-Nevanlinna–Pick kernels was first considered by Fang [Reference Fang9] who was able to show that the main results about the curvature invariant on the symmetric Fock space carry over to the Hardy space ![]() $H^2({\mathbb D}^k)$ over the polydisc. He also extended the theory to the invariant subspaces of the Dirichlet shift [Reference Fang8]. In the noncommutative setting, a notion of curvature invariant for noncommutative domains generated by positive regular free polynomials was considered in [Reference Popescu21].
$H^2({\mathbb D}^k)$ over the polydisc. He also extended the theory to the invariant subspaces of the Dirichlet shift [Reference Fang8]. In the noncommutative setting, a notion of curvature invariant for noncommutative domains generated by positive regular free polynomials was considered in [Reference Popescu21].
In [Reference Popescu22], we developed a theory of curvature invariant for the regular noncommutative polyball and formulated a theory of curvature and multiplicity invariants for the tensor product of full Fock spaces  $F^2(H_{n_1})\otimes \cdots \otimes F^2(H_{n_k})$ and also for the tensor product of symmetric Fock spaces. These results were used in [Reference Popescu24] to study the Euler characteristic associated with the elements of the regular noncommutative polyball and obtain an analogue of Arveson’s version of the Gauss–Bonnet–Chern theorem from Riemannian geometry, which connects the curvature to the Euler characteristic of some associated algebraic modules.
$F^2(H_{n_1})\otimes \cdots \otimes F^2(H_{n_k})$ and also for the tensor product of symmetric Fock spaces. These results were used in [Reference Popescu24] to study the Euler characteristic associated with the elements of the regular noncommutative polyball and obtain an analogue of Arveson’s version of the Gauss–Bonnet–Chern theorem from Riemannian geometry, which connects the curvature to the Euler characteristic of some associated algebraic modules.
We say that ![]() $V:=(V_1,\ldots, V_k)$,
$V:=(V_1,\ldots, V_k)$, ![]() $k\geq 2$, is a k-tuple of doubly
$k\geq 2$, is a k-tuple of doubly ![]() ${\mathcal U}$-commuting row isometries
${\mathcal U}$-commuting row isometries ![]() $V_i:=[V_{i,1}\cdots V_{i,n_i}]$ with
$V_i:=[V_{i,1}\cdots V_{i,n_i}]$ with ![]() $V_{i,s}\in B({\mathcal H})$ if
$V_{i,s}\in B({\mathcal H})$ if
 \begin{equation*}
V_{i,s} \in {\mathcal U}' \quad \text{and } \quad V_{i,s}^* V_{j,t}=U_{i,j}(s,t)^*V_{j,t}V_{i,s}^*\ \text{if } \ i\neq j,
\end{equation*}
\begin{equation*}
V_{i,s} \in {\mathcal U}' \quad \text{and } \quad V_{i,s}^* V_{j,t}=U_{i,j}(s,t)^*V_{j,t}V_{i,s}^*\ \text{if } \ i\neq j,
\end{equation*} where ![]() ${\mathcal U}:=\left\{U_{i,j}(s,t)\right\}\subset B({\mathcal H}) $ is a set of commuting unitary operators such that
${\mathcal U}:=\left\{U_{i,j}(s,t)\right\}\subset B({\mathcal H}) $ is a set of commuting unitary operators such that ![]() $U_{j,i}(t,s)=U_{i,j}(s,t)^*$ if i ≠ j and
$U_{j,i}(t,s)=U_{i,j}(s,t)^*$ if i ≠ j and ![]() ${\mathcal U}'$ is the commutant of
${\mathcal U}'$ is the commutant of ![]() ${\mathcal U}$. We note that, in the particular case when
${\mathcal U}$. We note that, in the particular case when ![]() $n_i=1$,
$n_i=1$, ![]() $V_1,\ldots, V_k$ are unitary operators, and
$V_1,\ldots, V_k$ are unitary operators, and ![]() $U_{i,j} :=\lambda_{i,j} I_{\mathcal H}$,
$U_{i,j} :=\lambda_{i,j} I_{\mathcal H}$, ![]() $\lambda_{i,j}\in {\mathbb T}$, the corresponding universal
$\lambda_{i,j}\in {\mathbb T}$, the corresponding universal ![]() $C^*$-algebras generated by
$C^*$-algebras generated by ![]() $V_1,\ldots, V_k$ are the higher-dimensional noncommutative tori which are studied in noncommutative differential geometry (see [Reference Connes4, Reference Rieffel30]). In the same setting, but assuming that
$V_1,\ldots, V_k$ are the higher-dimensional noncommutative tori which are studied in noncommutative differential geometry (see [Reference Connes4, Reference Rieffel30]). In the same setting, but assuming that ![]() $V_1,\ldots, V_k$ are isometries, De Jeu and Pinto [Reference De Jeu and Pinto5] obtained Wold decompositions for doubly
$V_1,\ldots, V_k$ are isometries, De Jeu and Pinto [Reference De Jeu and Pinto5] obtained Wold decompositions for doubly ![]() ${\mathcal U}$-commuting isometries. Inspired by their work, we studied in [Reference Popescu25, Reference Popescu26] the structure of the k-tuples of doubly
${\mathcal U}$-commuting isometries. Inspired by their work, we studied in [Reference Popescu25, Reference Popescu26] the structure of the k-tuples of doubly ![]() ${\Lambda}$-commuting row isometries, which corresponds to the particular case
${\Lambda}$-commuting row isometries, which corresponds to the particular case ![]() $U_{i,j}(s,t)=\lambda_{i,j}(s,t)I_{\mathcal H}$, where
$U_{i,j}(s,t)=\lambda_{i,j}(s,t)I_{\mathcal H}$, where ![]() $\lambda_{i,j}(s,t)\in {\mathbb T}$.
$\lambda_{i,j}(s,t)\in {\mathbb T}$.
The rotation algebras, noncommutative tori, the Heisenberg group ![]() $C^*$-algebras, as well as
$C^*$-algebras, as well as ![]() $C^*$-algebras generated by isometries with twisted commutation relations have been studied in the literature in various particular cases (see [Reference Anderson and Paschke1, Reference De Jeu and Pinto5, Reference Jorgensen, Proskurin and Samoilenko12, Reference Kabluchko13, Reference Kuzmin, Ostrovskyi, Proskurin, Weber and Yakymiv15, Reference Omland17–Reference Philips and Raeburn19, Reference Popescu25, Reference Proskurin29, Reference Weber31] and [Reference Popescu26]). More recently, we studied in [Reference Popescu27] the structure of the k-tuples of doubly
$C^*$-algebras generated by isometries with twisted commutation relations have been studied in the literature in various particular cases (see [Reference Anderson and Paschke1, Reference De Jeu and Pinto5, Reference Jorgensen, Proskurin and Samoilenko12, Reference Kabluchko13, Reference Kuzmin, Ostrovskyi, Proskurin, Weber and Yakymiv15, Reference Omland17–Reference Philips and Raeburn19, Reference Popescu25, Reference Proskurin29, Reference Weber31] and [Reference Popescu26]). More recently, we studied in [Reference Popescu27] the structure of the k-tuples of doubly ![]() ${\mathcal U}$-commuting row isometries, obtained Wold type decompositions [Reference Wold32], and used them to classify the k-tuples of doubly
${\mathcal U}$-commuting row isometries, obtained Wold type decompositions [Reference Wold32], and used them to classify the k-tuples of doubly ![]() ${\mathcal U}$-commuting row isometries up to a unitary equivalence. Furthermore, in [Reference Popescu28], we showed that many of the classical results concerning the dilation theory of contractions on Hilbert spaces have analogues for regular
${\mathcal U}$-commuting row isometries up to a unitary equivalence. Furthermore, in [Reference Popescu28], we showed that many of the classical results concerning the dilation theory of contractions on Hilbert spaces have analogues for regular ![]() ${\mathcal U}$-twisted polyballs.
${\mathcal U}$-twisted polyballs.
Due to the Wold decomposition from [Reference Popescu27], each k-tuple of doubly ![]() ${\mathcal U}$-commuting pure row isometries is unitarily equivalent to a standard multi-shift
${\mathcal U}$-commuting pure row isometries is unitarily equivalent to a standard multi-shift ![]() $\textbf{S}:=(\textbf{S}_1,\ldots, \textbf{S}_k)$ with
$\textbf{S}:=(\textbf{S}_1,\ldots, \textbf{S}_k)$ with ![]() $\textbf{S}_i:=[\textbf{S}_{i,1}\cdots \textbf{S}_{i,n_i}]$, which is a k-tuple of doubly
$\textbf{S}_i:=[\textbf{S}_{i,1}\cdots \textbf{S}_{i,n_i}]$, which is a k-tuple of doubly ![]() $I\otimes{\mathcal U}$-commuting pure row isometries on the Hilbert space
$I\otimes{\mathcal U}$-commuting pure row isometries on the Hilbert space  $\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal H}$, where
$\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal H}$, where  ${\mathbb F}_{n_i}^+$ is the unital free semigroup with ni generators (see
${\mathbb F}_{n_i}^+$ is the unital free semigroup with ni generators (see ![]() $\S$ 3 for the definition). It was proved in [Reference Popescu28] that the standard multi-shift plays the role of a universal model for the pure elements in the
$\S$ 3 for the definition). It was proved in [Reference Popescu28] that the standard multi-shift plays the role of a universal model for the pure elements in the ![]() ${\mathcal U}$-twisted polyball. To present this result, we introduce the
${\mathcal U}$-twisted polyball. To present this result, we introduce the ![]() ${\mathcal U}$-twisted polyball
${\mathcal U}$-twisted polyball  $\textbf{B}^{\mathcal U}({\mathcal H})$ as the set of all
$\textbf{B}^{\mathcal U}({\mathcal H})$ as the set of all ![]() ${\mathcal U}$-commuting k-tuples
${\mathcal U}$-commuting k-tuples ![]() $A:=(A_1,\ldots, A_k)$ of row contractions
$A:=(A_1,\ldots, A_k)$ of row contractions ![]() $A_i:=(A_{i,1},\ldots, A_{i,n_i})\in B({\mathcal H})^{n_i}$, i.e.
$A_i:=(A_{i,1},\ldots, A_{i,n_i})\in B({\mathcal H})^{n_i}$, i.e.
We proved in [Reference Popescu28] that  $A\in \textbf{B}^{\mathcal U}({\mathcal H})$ is a pure element, i.e.
$A\in \textbf{B}^{\mathcal U}({\mathcal H})$ is a pure element, i.e.  $\Phi_{A_i}^m(I)\to 0$ strongly as
$\Phi_{A_i}^m(I)\to 0$ strongly as ![]() $m\to \infty$, where
$m\to \infty$, where ![]() $\Phi_{A_i}:B({\mathcal H})\to B({\mathcal H}) $ is the completely positive linear map defined by
$\Phi_{A_i}:B({\mathcal H})\to B({\mathcal H}) $ is the completely positive linear map defined by  $\Phi_{A_i}(X):=\sum_{s=1}^{n_i} A_{i,s} XA_{i,s}^*,$ and the defect operator
$\Phi_{A_i}(X):=\sum_{s=1}^{n_i} A_{i,s} XA_{i,s}^*,$ and the defect operator
if and only if there are a Hilbert space ![]() ${\mathcal D}\subset {\mathcal H}$ and a multi-shift
${\mathcal D}\subset {\mathcal H}$ and a multi-shift ![]() $\textbf{S}:=(\textbf{S}_1,\ldots, \textbf{S}_k)$ with
$\textbf{S}:=(\textbf{S}_1,\ldots, \textbf{S}_k)$ with ![]() $\textbf{S}_i:=[\textbf{S}_{i,1}\cdots \textbf{S}_{i,n_i}]$ of doubly
$\textbf{S}_i:=[\textbf{S}_{i,1}\cdots \textbf{S}_{i,n_i}]$ of doubly ![]() $I \otimes {\mathcal U}$-commuting pure isometries on the Hilbert space
$I \otimes {\mathcal U}$-commuting pure isometries on the Hilbert space  $\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal D}$ such that
$\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal D}$ such that ![]() ${\mathcal H}$ is co-invariant under all operators Si,s and
${\mathcal H}$ is co-invariant under all operators Si,s and ![]() $I\otimes U_{i,j}(s,t)$ and
$I\otimes U_{i,j}(s,t)$ and ![]() $A_{i,s}^*=\textbf{S}_{i,s}^*|_{\mathcal H}.
$ Due to this reason, to understand the structure of pure elements A in the
$A_{i,s}^*=\textbf{S}_{i,s}^*|_{\mathcal H}.
$ Due to this reason, to understand the structure of pure elements A in the ![]() ${\mathcal U}$-twisted polyball
${\mathcal U}$-twisted polyball  $\textbf{B}^{\mathcal U}({\mathcal H})$ with positive defect operators
$\textbf{B}^{\mathcal U}({\mathcal H})$ with positive defect operators ![]() $\Delta_A(I)$, one should focus on the
$\Delta_A(I)$, one should focus on the ![]() $I \otimes {\mathcal U}$-twisted multi-shifts S and the closed invariant (resp. co-invariant subspaces) under S and
$I \otimes {\mathcal U}$-twisted multi-shifts S and the closed invariant (resp. co-invariant subspaces) under S and ![]() $I\otimes {\mathcal U}$.
$I\otimes {\mathcal U}$.
The goal of the present paper is to show that the notion of curvature admits a natural extension to the framework of ![]() ${\mathcal U}$-twisted polyballs and to present its basic properties followed by several consequences. We remark that if
${\mathcal U}$-twisted polyballs and to present its basic properties followed by several consequences. We remark that if ![]() ${\mathcal U}\neq \{I\}$, the row contractions
${\mathcal U}\neq \{I\}$, the row contractions ![]() $A_1,\ldots, A_k$ are not pairwise commuting. Due to this reason, the ‘tensor product’ techniques used in the theory of the regular polyballs and the curvature [Reference Popescu22, Reference Popescu23] need to be replaced with new ones appropriate for the
$A_1,\ldots, A_k$ are not pairwise commuting. Due to this reason, the ‘tensor product’ techniques used in the theory of the regular polyballs and the curvature [Reference Popescu22, Reference Popescu23] need to be replaced with new ones appropriate for the ![]() ${\mathcal U}$-twisted polyballs [Reference Popescu27, Reference Popescu28].
${\mathcal U}$-twisted polyballs [Reference Popescu27, Reference Popescu28].
In ![]() $\S$ 2, after a few preliminary results, we introduce (see Definition (2.7)) and prove the existence of the M-curvature, where
$\S$ 2, after a few preliminary results, we introduce (see Definition (2.7)) and prove the existence of the M-curvature, where  $M=(M_1,\ldots, M_k)\in {\mathbb R}_+^k$,
$M=(M_1,\ldots, M_k)\in {\mathbb R}_+^k$,  $M_i\geq \|\Phi^*_{A_i}(I)\| \gt 0$, and
$M_i\geq \|\Phi^*_{A_i}(I)\| \gt 0$, and  $ \Phi^*_{A_i}(X):=\sum_{j=1}^{n_i} A^*_iXA_i$, associated with any k-tuple
$ \Phi^*_{A_i}(X):=\sum_{j=1}^{n_i} A^*_iXA_i$, associated with any k-tuple ![]() $A:=(A_1,\ldots, A_k)$ of
$A:=(A_1,\ldots, A_k)$ of ![]() ${\mathcal U}$-commuting operators with positive trace class defect
${\mathcal U}$-commuting operators with positive trace class defect ![]() $\Delta_A(I)$ and show that
$\Delta_A(I)$ and show that
We also show that if A and A ʹ are k-tuples of ![]() ${\mathcal U}$-commuting and
${\mathcal U}$-commuting and ![]() ${\mathcal U}'$-commuting operators, respectively, with positive trace class defect operators, then
${\mathcal U}'$-commuting operators, respectively, with positive trace class defect operators, then ![]() $A\oplus A' $ is a k-tuple of
$A\oplus A' $ is a k-tuple of ![]() ${\mathcal U}\oplus {\mathcal U}'$-commuting operators with a positive trace class defect operator and
${\mathcal U}\oplus {\mathcal U}'$-commuting operators with a positive trace class defect operator and
If, in addition, ![]() $\dim{\mathcal H}' \lt \infty$, then
$\dim{\mathcal H}' \lt \infty$, then ![]() $\mathrm{curv}_M({A}\oplus {A}')=\mathrm{curv}_M({A})$.
$\mathrm{curv}_M({A}\oplus {A}')=\mathrm{curv}_M({A})$.
In ![]() $\S$ 3, under the assumption that A is in the
$\S$ 3, under the assumption that A is in the ![]() ${\mathcal U}$-twisted polyball
${\mathcal U}$-twisted polyball ![]() $ B^{\mathcal U}({\mathcal H})$ and has positive trace class defect operator
$ B^{\mathcal U}({\mathcal H})$ and has positive trace class defect operator ![]() $\Delta_A(I)$, we established several asymptotic formulas for the M-curvature invariant
$\Delta_A(I)$, we established several asymptotic formulas for the M-curvature invariant ![]() $ \mathrm{curv}_M (A)$ in terms of the noncommutative Berezin kernel KA associated with A.
$ \mathrm{curv}_M (A)$ in terms of the noncommutative Berezin kernel KA associated with A.
Throughout this paper, special attention is given to the case ![]() $M=(n_1,\ldots, n_k)$, when the corresponding curvature, denote by
$M=(n_1,\ldots, n_k)$, when the corresponding curvature, denote by ![]() $\mathrm{curv}(A)$, satisfies the asymptotic formula
$\mathrm{curv}(A)$, satisfies the asymptotic formula
 \begin{equation*} \mathrm{curv}({A})=
\lim_{m\to\infty}\frac{1}{\left(\begin{matrix} m+k\\ k\end{matrix}\right)}\sum_{{q_1\geq 0,\ldots, q_k\geq 0}\atop {q_1+\cdots +q_k\leq m}} \frac{
\mathrm{trace\,}\left[ {K_{A}^*} (P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal H}){K_{A}}\right]}
{\mathrm{trace\,}P_{(q_1,\ldots, q_k)}},
\end{equation*}
\begin{equation*} \mathrm{curv}({A})=
\lim_{m\to\infty}\frac{1}{\left(\begin{matrix} m+k\\ k\end{matrix}\right)}\sum_{{q_1\geq 0,\ldots, q_k\geq 0}\atop {q_1+\cdots +q_k\leq m}} \frac{
\mathrm{trace\,}\left[ {K_{A}^*} (P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal H}){K_{A}}\right]}
{\mathrm{trace\,}P_{(q_1,\ldots, q_k)}},
\end{equation*} where ![]() $P_{(q_1,\ldots, q_k)}$ is the orthogonal projection of
$P_{(q_1,\ldots, q_k)}$ is the orthogonal projection of  $\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)$, with orthonormal basis
$\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)$, with orthonormal basis ![]() $\{\chi_{ (\alpha_1,\ldots, \alpha_k)}\}$, onto the subspace
$\{\chi_{ (\alpha_1,\ldots, \alpha_k)}\}$, onto the subspace  $
\mathrm{span}\, \{\chi_{ (\alpha_1,\ldots, \alpha_k)}: \ \alpha_i\in {\mathbb F}_{n_i}^+, |\alpha_i|=q_i\}.
$ We provide several asymptotic formulas including
$
\mathrm{span}\, \{\chi_{ (\alpha_1,\ldots, \alpha_k)}: \ \alpha_i\in {\mathbb F}_{n_i}^+, |\alpha_i|=q_i\}.
$ We provide several asymptotic formulas including
 \begin{equation*} \mathrm{curv}({A})= \lim_{q_1\to\infty}\cdots\lim_{q_k\to\infty}
\frac{\mathrm{trace\,}\left[(id-\Phi_{A_1}^{q_1+1})\circ \cdots \circ (id-\Phi_{A_k}^{q_k+1})(I)\right]}
{\prod_{i=1}^k(1+n_i+\cdots + n_i^{q_i})},
\end{equation*}
\begin{equation*} \mathrm{curv}({A})= \lim_{q_1\to\infty}\cdots\lim_{q_k\to\infty}
\frac{\mathrm{trace\,}\left[(id-\Phi_{A_1}^{q_1+1})\circ \cdots \circ (id-\Phi_{A_k}^{q_k+1})(I)\right]}
{\prod_{i=1}^k(1+n_i+\cdots + n_i^{q_i})},
\end{equation*} where ![]() $\Phi_{A_i}$ is the completely positive linear map associated with the row contraction Ai. We also show that the curvature invariant is upper semi-continuous.
$\Phi_{A_i}$ is the completely positive linear map associated with the row contraction Ai. We also show that the curvature invariant is upper semi-continuous.
The standard multi-shift ![]() $\textbf{S}_\textbf{z}$ associated with the scalar weights
$\textbf{S}_\textbf{z}$ associated with the scalar weights ![]() $\textbf{z}=(z_{i,j}(s,t))$, where
$\textbf{z}=(z_{i,j}(s,t))$, where ![]() $z_{i,j}(s,t)\in {\mathbb T}$ and
$z_{i,j}(s,t)\in {\mathbb T}$ and  $z_{j,i}(t,s)=\overline{z_{i,j}(s,t})$, plays an important role in this paper. This is due to the fact that any pure element A in the
$z_{j,i}(t,s)=\overline{z_{i,j}(s,t})$, plays an important role in this paper. This is due to the fact that any pure element A in the ![]() ${\mathcal U}$-twisted polyball with the property that
${\mathcal U}$-twisted polyball with the property that ![]() $\Delta_A(I)\geq 0$ and
$\Delta_A(I)\geq 0$ and ![]() $\mathrm{rank}\,\Delta_A(I)=m\in {\mathbb N}$ is the compression of a direct sum
$\mathrm{rank}\,\Delta_A(I)=m\in {\mathbb N}$ is the compression of a direct sum ![]() $\oplus_{p=1}^m \textbf{S}_{\textbf{z}^{(p)}}$ of scalar multi-shifts to a co-invariant subspace
$\oplus_{p=1}^m \textbf{S}_{\textbf{z}^{(p)}}$ of scalar multi-shifts to a co-invariant subspace ![]() ${\mathcal M}^\perp$, i.e.
${\mathcal M}^\perp$, i.e. ![]() $A_{i,s}=P_{{\mathcal M}^\perp} ( \textbf{S}_{\textbf{z}^{(p)}})_{i,s}|_{{\mathcal M}^\perp}$.
$A_{i,s}=P_{{\mathcal M}^\perp} ( \textbf{S}_{\textbf{z}^{(p)}})_{i,s}|_{{\mathcal M}^\perp}$.
Unlike the non-twisted case (![]() ${\mathcal U}=\{I\}$) where we have, up to a unitary equivalence, just one standard shift S with
${\mathcal U}=\{I\}$) where we have, up to a unitary equivalence, just one standard shift S with ![]() $\mathrm{rank}\,\Delta_\textbf{S}(I)=1$, in the twisted case, all the multi-shifts
$\mathrm{rank}\,\Delta_\textbf{S}(I)=1$, in the twisted case, all the multi-shifts ![]() $\textbf{S}_\textbf{z}$ satisfy the relation
$\textbf{S}_\textbf{z}$ satisfy the relation
and these are the only ![]() ${\mathcal U}$-twisted multi-shifts S with
${\mathcal U}$-twisted multi-shifts S with ![]() $\mathrm{rank}\,\Delta_\textbf{S}(I)=1$. Moreover, we prove, in
$\mathrm{rank}\,\Delta_\textbf{S}(I)=1$. Moreover, we prove, in ![]() $\S$ 4, that if
$\S$ 4, that if ![]() $\textbf{S}_{\mathcal U}$ and
$\textbf{S}_{\mathcal U}$ and ![]() $\textbf{S}_{{\mathcal U}'}$ are the standard multi-shifts associated with
$\textbf{S}_{{\mathcal U}'}$ are the standard multi-shifts associated with ![]() ${\mathcal U}\subset B({\mathcal H})$ and
${\mathcal U}\subset B({\mathcal H})$ and ![]() ${\mathcal U}'\subset B({\mathcal H}')$, respectively, then
${\mathcal U}'\subset B({\mathcal H}')$, respectively, then ![]() $\textbf{S}_{\mathcal U}$ is jointly similar to
$\textbf{S}_{\mathcal U}$ is jointly similar to ![]() $\textbf{S}_{{\mathcal U}'}$ if and only if there is an invertible operator
$\textbf{S}_{{\mathcal U}'}$ if and only if there is an invertible operator ![]() $W\in B({\mathcal H},{\mathcal H}')$ such that
$W\in B({\mathcal H},{\mathcal H}')$ such that  $U_{i,j}(s,t)=W^{-1}U_{i,j}'(s,t)W$. Consequently, if
$U_{i,j}(s,t)=W^{-1}U_{i,j}'(s,t)W$. Consequently, if ![]() $\textbf{S}_\textbf{z}$ and
$\textbf{S}_\textbf{z}$ and ![]() $\textbf{S}_\textbf{z'}$ are standard multi-shifts associated with the scalar weights z and
$\textbf{S}_\textbf{z'}$ are standard multi-shifts associated with the scalar weights z and ![]() $\textbf{z}'$, respectively, then they are unitarily equivalent if and only if
$\textbf{z}'$, respectively, then they are unitarily equivalent if and only if ![]() $\textbf{z}=\textbf{z'}$.
$\textbf{z}=\textbf{z'}$.
In ![]() $\S$ 5, we prove that if A is an element in the
$\S$ 5, we prove that if A is an element in the ![]() ${\mathcal U}$-twisted polyball
${\mathcal U}$-twisted polyball  $ \textbf{B}^{\mathcal U}({\mathcal H})$ such that it admits characteristic function
$ \textbf{B}^{\mathcal U}({\mathcal H})$ such that it admits characteristic function ![]() $\Theta_A$ and the defect
$\Theta_A$ and the defect ![]() $\Delta_A(I)$ is a positive finite rank operator, then the curvature operator
$\Delta_A(I)$ is a positive finite rank operator, then the curvature operator ![]() $ \Delta_\textbf{S}(K_A K_A^*) (N\otimes I_{\mathcal H}) $ is a trace class and
$ \Delta_\textbf{S}(K_A K_A^*) (N\otimes I_{\mathcal H}) $ is a trace class and
where
 \begin{equation*}
N:=\sum_{(s_1,\ldots, s_k)\in {\mathbb Z}_+^k} \frac{1}{n_1^{s_1}\cdots n_k^{s_k}}
P_{(s_1,\ldots, s_k)}.
\end{equation*}
\begin{equation*}
N:=\sum_{(s_1,\ldots, s_k)\in {\mathbb Z}_+^k} \frac{1}{n_1^{s_1}\cdots n_k^{s_k}}
P_{(s_1,\ldots, s_k)}.
\end{equation*}This leads to the index type formula
which is used to show that the curvature invariant detects the elements in ![]() $B({\mathcal H})^{n_1+\cdots + n_k}$ which are unitarily equivalent to an
$B({\mathcal H})^{n_1+\cdots + n_k}$ which are unitarily equivalent to an ![]() $I\otimes{\mathcal U}$-twisted multi-shift S of finite rank defect operator, i.e. acting on the Hilbert space
$I\otimes{\mathcal U}$-twisted multi-shift S of finite rank defect operator, i.e. acting on the Hilbert space  $\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal K}$ with
$\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal K}$ with ![]() $\dim {\mathcal K} \lt \infty$ (see theorem 5.5).
$\dim {\mathcal K} \lt \infty$ (see theorem 5.5).
In ![]() $\S$ 6, under the assumption that S is a
$\S$ 6, under the assumption that S is a ![]() $I\otimes{\mathcal U}$-twisted multi-shift on
$I\otimes{\mathcal U}$-twisted multi-shift on  $ \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal H}$ with
$ \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal H}$ with ![]() $\dim {\mathcal H} \lt \infty$ and
$\dim {\mathcal H} \lt \infty$ and ![]() ${\mathcal M}$ is any invariant subspace under S and
${\mathcal M}$ is any invariant subspace under S and ![]() $I\otimes {\mathcal U}$, we introduce the multiplicity of
$I\otimes {\mathcal U}$, we introduce the multiplicity of ![]() ${\mathcal M}$ by setting
${\mathcal M}$ by setting
 \begin{equation*}
m({\mathcal M}):=
\lim_{m\to\infty}\frac{1}{\left(\begin{matrix} m+k\\ k\end{matrix}\right)}\sum_{{q_1\geq 0,\ldots, q_k\geq 0}\atop {q_1+\cdots +q_k\leq m}} \frac{
\mathrm{trace\,}\left[ P_{\mathcal M} (P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal H}) \right]}
{\mathrm{trace\,}P_{(q_1,\ldots, q_k)}}.
\end{equation*}
\begin{equation*}
m({\mathcal M}):=
\lim_{m\to\infty}\frac{1}{\left(\begin{matrix} m+k\\ k\end{matrix}\right)}\sum_{{q_1\geq 0,\ldots, q_k\geq 0}\atop {q_1+\cdots +q_k\leq m}} \frac{
\mathrm{trace\,}\left[ P_{\mathcal M} (P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal H}) \right]}
{\mathrm{trace\,}P_{(q_1,\ldots, q_k)}}.
\end{equation*}We prove its existence, provide several asymptotic formulas, and connect it to the curvature invariant by showing that
In particular, if ![]() $\textbf{S}_\textbf{z}$ is the scalar z-twisted multi-shift on
$\textbf{S}_\textbf{z}$ is the scalar z-twisted multi-shift on  $\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)$ and
$\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)$ and ![]() ${\mathcal M}$ is an invariant subspace under
${\mathcal M}$ is an invariant subspace under ![]() $\textbf{S}_\textbf{z}\otimes I_{\mathcal E}$ with
$\textbf{S}_\textbf{z}\otimes I_{\mathcal E}$ with ![]() $\dim{\mathcal E} \lt \infty$, then its multiplicity exists. We remark that if
$\dim{\mathcal E} \lt \infty$, then its multiplicity exists. We remark that if ![]() $n_1=\cdots=n_k=1$, then
$n_1=\cdots=n_k=1$, then ![]() ${\mathcal M}$ is in the vector-valued Hardy space
${\mathcal M}$ is in the vector-valued Hardy space ![]() $H^2({\mathbb D}^k)\otimes {\mathcal E}$ and
$H^2({\mathbb D}^k)\otimes {\mathcal E}$ and
 \begin{equation*}
m({\mathcal M})=\lim_{m\to\infty}\frac{\mathrm{trace\,}[P_{\mathcal M} (P_{\leq m}\otimes I_{\mathcal E})]}{\mathrm{trace\,}[P_{\leq m}]},
\end{equation*}
\begin{equation*}
m({\mathcal M})=\lim_{m\to\infty}\frac{\mathrm{trace\,}[P_{\mathcal M} (P_{\leq m}\otimes I_{\mathcal E})]}{\mathrm{trace\,}[P_{\leq m}]},
\end{equation*} where ![]() $P_{\leq m}$ is the orthogonal projection on the polynomials of degree
$P_{\leq m}$ is the orthogonal projection on the polynomials of degree ![]() $\leq m$. This is a twisted version of Fang’s [Reference Fang9] commutative result for
$\leq m$. This is a twisted version of Fang’s [Reference Fang9] commutative result for ![]() $H^2({\mathbb D}^k)\otimes {\mathcal E}$ when
$H^2({\mathbb D}^k)\otimes {\mathcal E}$ when ![]() $\textbf{z}=\{1\}$.
$\textbf{z}=\{1\}$.
In ![]() $\S$ 6, we also obtain some results concerning the semi-continuity for the curvature and the multiplicity invariants. More precisely, we prove that if S is a
$\S$ 6, we also obtain some results concerning the semi-continuity for the curvature and the multiplicity invariants. More precisely, we prove that if S is a ![]() ${\mathcal U}$-twisted multi-shift with
${\mathcal U}$-twisted multi-shift with ![]() ${\mathcal U}\subset B({\mathcal H})$ and
${\mathcal U}\subset B({\mathcal H})$ and ![]() $\dim {\mathcal H} \lt \infty$, acting on
$\dim {\mathcal H} \lt \infty$, acting on  $\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal H}$, and
$\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal H}$, and ![]() ${\mathcal M}$ and
${\mathcal M}$ and ![]() ${\mathcal M}_p$ are invariant subspaces of S and
${\mathcal M}_p$ are invariant subspaces of S and ![]() ${\mathcal U}$ such that
${\mathcal U}$ such that ![]() $ P_{{\mathcal M}_p}\to P_{\mathcal M}$ in the weak operator topology, then
$ P_{{\mathcal M}_p}\to P_{\mathcal M}$ in the weak operator topology, then
 \begin{equation*}
\limsup_{p\to\infty}\mathrm{curv} (P_{{\mathcal M}_p^\perp} \textbf{S}|_{{\mathcal M}_p^\perp})\leq
\mathrm{curv} (P_{{\mathcal M}^\perp} \textbf{S}|_{{\mathcal M}^\perp})
\end{equation*}
\begin{equation*}
\limsup_{p\to\infty}\mathrm{curv} (P_{{\mathcal M}_p^\perp} \textbf{S}|_{{\mathcal M}_p^\perp})\leq
\mathrm{curv} (P_{{\mathcal M}^\perp} \textbf{S}|_{{\mathcal M}^\perp})
\end{equation*}and
 \begin{equation*}
\liminf_{p\to\infty}m({\mathcal M}_p)\geq m({\mathcal M}).
\end{equation*}
\begin{equation*}
\liminf_{p\to\infty}m({\mathcal M}_p)\geq m({\mathcal M}).
\end{equation*} If ![]() ${\mathcal M}$ is a Beurling type invariant subspace under S and
${\mathcal M}$ is a Beurling type invariant subspace under S and ![]() $I\otimes {\mathcal U}$, which does not contain nontrivial reducing subspace under S, then we show that the multiplicity operator
$I\otimes {\mathcal U}$, which does not contain nontrivial reducing subspace under S, then we show that the multiplicity operator ![]() $\Delta_\textbf{S}(P_{\mathcal M})(N\otimes I)$ is a trace class and
$\Delta_\textbf{S}(P_{\mathcal M})(N\otimes I)$ is a trace class and
In particular, this relation holds for the Beurling type invariant subspace under ![]() $\textbf{S}_\textbf{z}\otimes I_{\mathcal E}$ with
$\textbf{S}_\textbf{z}\otimes I_{\mathcal E}$ with ![]() $\dim{\mathcal E} \lt \infty$.
$\dim{\mathcal E} \lt \infty$.
We remark that if A is an element in  $\textbf{B}^{{\mathcal U}}({\mathcal H})$ and
$\textbf{B}^{{\mathcal U}}({\mathcal H})$ and ![]() ${\mathcal M}$ is an invariant subspace under A and
${\mathcal M}$ is an invariant subspace under A and ![]() ${\mathcal U}$, then
${\mathcal U}$, then ![]() $A|_{\mathcal M}$ is not necessarily in the
$A|_{\mathcal M}$ is not necessarily in the ![]() ${\mathcal U}|_{\mathcal M}$-twisted polyball in general. However, we will provide necessary and sufficient conditions when
${\mathcal U}|_{\mathcal M}$-twisted polyball in general. However, we will provide necessary and sufficient conditions when ![]() $A|_{\mathcal M}$ is in
$A|_{\mathcal M}$ is in  $\textbf{B}^{{\mathcal U}|_{\mathcal M}}({\mathcal H})$ and prove a stability result for the curvature invariant.
$\textbf{B}^{{\mathcal U}|_{\mathcal M}}({\mathcal H})$ and prove a stability result for the curvature invariant.
In ![]() $\S$ 7, we present some results concerning the range of the curvature and the multiplicity invariants. More precisely, we show that if
$\S$ 7, we present some results concerning the range of the curvature and the multiplicity invariants. More precisely, we show that if ![]() $(n_1,\ldots, n_k)\in {\mathbb N}^k$ with
$(n_1,\ldots, n_k)\in {\mathbb N}^k$ with ![]() $n_j\geq 2$ for some j and
$n_j\geq 2$ for some j and ![]() $t\in [0,m]$, then there exists a pure element A in the
$t\in [0,m]$, then there exists a pure element A in the ![]() ${\mathcal U}$-twisted polyball such that
${\mathcal U}$-twisted polyball such that ![]() $\mathrm{rank}\, A=m$ and
$\mathrm{rank}\, A=m$ and ![]() $\mathrm{curv}(A)=t$. Consequently, the range of the curvature on the
$\mathrm{curv}(A)=t$. Consequently, the range of the curvature on the ![]() ${\mathcal U}$-twisted polyballs is
${\mathcal U}$-twisted polyballs is ![]() $[0,\infty)$. This also implies that the range of the multiplicity invariant is
$[0,\infty)$. This also implies that the range of the multiplicity invariant is ![]() $[0,\infty)$.
$[0,\infty)$.
On the other hand, we show that the range of the curvature restricted to the class of doubly ![]() ${\mathcal U}$-commuting row isometries with trace class defect operators is
${\mathcal U}$-commuting row isometries with trace class defect operators is ![]() ${\mathbb Z}_+$. In addition, if
${\mathbb Z}_+$. In addition, if ![]() $V:=(V_1,\ldots, V_k)$ with
$V:=(V_1,\ldots, V_k)$ with ![]() $V_i:=[V_{i,1}\cdots V_{i,n_i}]$ and
$V_i:=[V_{i,1}\cdots V_{i,n_i}]$ and ![]() $V_{i,s}\in B({\mathcal H})$ is a k-tuple of doubly
$V_{i,s}\in B({\mathcal H})$ is a k-tuple of doubly ![]() ${\mathcal U}$-commuting row isometries with the trace class defect operator, we prove that
${\mathcal U}$-commuting row isometries with the trace class defect operator, we prove that
and
 \begin{equation*}
\mathrm{curv} (V)=m\in {\mathbb Z}_+\quad \text{ if and only if } \quad \dim \bigcap_{{i\in \{1,\ldots, k\}}\atop{s\in \{1,\ldots, n_i\}}} \ker V_{i,s}^*=m.
\end{equation*}
\begin{equation*}
\mathrm{curv} (V)=m\in {\mathbb Z}_+\quad \text{ if and only if } \quad \dim \bigcap_{{i\in \{1,\ldots, k\}}\atop{s\in \{1,\ldots, n_i\}}} \ker V_{i,s}^*=m.
\end{equation*} Moreover, if ![]() $\mathrm{curv} (V)\neq 0$ and
$\mathrm{curv} (V)\neq 0$ and ![]() $n_j\geq 2$ for some
$n_j\geq 2$ for some ![]() $j\in \{1,\ldots, k\}$, then we prove that, for any
$j\in \{1,\ldots, k\}$, then we prove that, for any ![]() $t\in [0, \mathrm{curv} (V)]$, there is an invariant subspace
$t\in [0, \mathrm{curv} (V)]$, there is an invariant subspace ![]() ${\mathcal M}\subset {\mathcal H}$ under V and
${\mathcal M}\subset {\mathcal H}$ under V and ![]() ${\mathcal U}$ such that
${\mathcal U}$ such that ![]() $\mathrm{curv} (P_{{\mathcal M}^\perp}V|_{{\mathcal M}^\perp})=t$.
$\mathrm{curv} (P_{{\mathcal M}^\perp}V|_{{\mathcal M}^\perp})=t$.
In the sequel to this paper, we study the Euler characteristic associated with the elements of the ![]() ${\mathcal U}$-twisted polyballs and obtain an analogue of Arveson’s version of the Gauss–Bonnet–Chern theorem from Riemannian geometry.
${\mathcal U}$-twisted polyballs and obtain an analogue of Arveson’s version of the Gauss–Bonnet–Chern theorem from Riemannian geometry.
2. Curvature invariant for  ${\mathcal U}$-commuting operators
${\mathcal U}$-commuting operators
In this section, we consider a few preliminary results which are needed throughout the paper, introduce and prove the existence of the M-curvature, and present several asymptotic formulas and basic properties for the curvature invariant.
Let ![]() $k\in {\mathbb N}:=\{1,2,\ldots\}$ with
$k\in {\mathbb N}:=\{1,2,\ldots\}$ with ![]() $k\geq 2$, and consider the set
$k\geq 2$, and consider the set
where ![]() $n_i, n_j\in {\mathbb N}$. Throughout this paper,
$n_i, n_j\in {\mathbb N}$. Throughout this paper,  ${\mathcal U}:=\left\{U_{i,j}(s,t)\right\}_{(i,j,s,t)\in \Gamma}$ is a set of commuting unitary operators on a Hilbert space such that
${\mathcal U}:=\left\{U_{i,j}(s,t)\right\}_{(i,j,s,t)\in \Gamma}$ is a set of commuting unitary operators on a Hilbert space such that
Definition. A k-tuple ![]() $A:=(A_1,\ldots, A_k)\in B({\mathcal H})^{n_1+\cdots +n_k}$ with
$A:=(A_1,\ldots, A_k)\in B({\mathcal H})^{n_1+\cdots +n_k}$ with ![]() $A_i:=(A_{i,1},\ldots, A_{i,n_i})$ is called
$A_i:=(A_{i,1},\ldots, A_{i,n_i})$ is called ![]() ${\mathcal U}$-commuting if
${\mathcal U}$-commuting if
where ![]() ${\mathcal U}'$ is the commutant of
${\mathcal U}'$ is the commutant of ![]() ${\mathcal U}\subset B({\mathcal H})$. If, in addition,
${\mathcal U}\subset B({\mathcal H})$. If, in addition,
we say that A is a k-tuple of doubly ![]() ${\mathcal U}$-commuting operators.
${\mathcal U}$-commuting operators.
Definition. The ![]() ${\mathcal U}$-twisted polyball
${\mathcal U}$-twisted polyball  $\textbf{B}^{\mathcal U}({\mathcal H})$ is the set of all
$\textbf{B}^{\mathcal U}({\mathcal H})$ is the set of all ![]() ${\mathcal U}$-commuting k-tuples
${\mathcal U}$-commuting k-tuples ![]() $A:=(A_1,\ldots, A_k)$ of row contractions
$A:=(A_1,\ldots, A_k)$ of row contractions ![]() $A_i:=(A_{i,1},\ldots, A_{i,n_i})\in B({\mathcal H})^{n_i}$, i.e.
$A_i:=(A_{i,1},\ldots, A_{i,n_i})\in B({\mathcal H})^{n_i}$, i.e.
 \begin{equation*}A_{i,1}A_{i,1}^*+\cdots +A_{i,n_i}A_{i,n_i}^*\leq I.\end{equation*}
\begin{equation*}A_{i,1}A_{i,1}^*+\cdots +A_{i,n_i}A_{i,n_i}^*\leq I.\end{equation*} We say that A has a positive defect operator if ![]() $\Delta_{A}(I)\geq 0$, where
$\Delta_{A}(I)\geq 0$, where
and ![]() $\Phi_{A_i}:B({\mathcal H})\to B({\mathcal H}) $ is the completely positive linear map defined by
$\Phi_{A_i}:B({\mathcal H})\to B({\mathcal H}) $ is the completely positive linear map defined by  $
\Phi_{A_i}(X):=\sum_{s=1}^{n_i} A_{i.s} XA_{i,s}^*.
$
$
\Phi_{A_i}(X):=\sum_{s=1}^{n_i} A_{i.s} XA_{i,s}^*.
$
The regular ![]() ${\mathcal U}$-twisted polyball
${\mathcal U}$-twisted polyball  $\textbf{B}^{\mathcal U}_{reg}({\mathcal H})$ is the set of all k-tuples A of
$\textbf{B}^{\mathcal U}_{reg}({\mathcal H})$ is the set of all k-tuples A of ![]() ${\mathcal U}$-commuting row contractions such that
${\mathcal U}$-commuting row contractions such that ![]() $
\Delta_{rA}(I)\geq 0$ for any
$
\Delta_{rA}(I)\geq 0$ for any ![]() $ r\in [0,1)$.
$ r\in [0,1)$.
According to Proposition 1.2 from [Reference Popescu28], a k-tuple A of ![]() ${\mathcal U}$-commuting row contractions is in
${\mathcal U}$-commuting row contractions is in  $\textbf{B}^{\mathcal U}_{reg}({\mathcal H})$ if and only if
$\textbf{B}^{\mathcal U}_{reg}({\mathcal H})$ if and only if ![]() $(id-\Phi_{A_1})^{s_1}\circ\cdots \circ (id-\Phi_{A_k})^{s_k}(I)\geq 0$ for any
$(id-\Phi_{A_1})^{s_1}\circ\cdots \circ (id-\Phi_{A_k})^{s_k}(I)\geq 0$ for any ![]() $ s_1,\ldots, s_k\in \{0,1\}$. We note that
$ s_1,\ldots, s_k\in \{0,1\}$. We note that  $\textbf{B}^{\mathcal U}_{reg}({\mathcal H})$ is included in
$\textbf{B}^{\mathcal U}_{reg}({\mathcal H})$ is included in  $ \textbf{B}^{\mathcal U}({\mathcal H})$ and the inclusion is strict in general. On the other hand, it is easy to see that if
$ \textbf{B}^{\mathcal U}({\mathcal H})$ and the inclusion is strict in general. On the other hand, it is easy to see that if  $A\in \textbf{B}^{\mathcal U}_{reg}({\mathcal H})$, then
$A\in \textbf{B}^{\mathcal U}_{reg}({\mathcal H})$, then  $(z_1A_1,\ldots, z_kA_k)\in \textbf{B}^{\mathcal U}_{reg}({\mathcal H})$ for any
$(z_1A_1,\ldots, z_kA_k)\in \textbf{B}^{\mathcal U}_{reg}({\mathcal H})$ for any ![]() $z_i\in {\mathbb D}:=\{z\in {\mathbb C}:\ |z|\leq 1\}$.
$z_i\in {\mathbb D}:=\{z\in {\mathbb C}:\ |z|\leq 1\}$.
Proposition 2.3. If ![]() $A:=(A_1,\ldots, A_k)\in B({\mathcal H})^{n_1+\cdots + n_k}$ is a k-tuple of
$A:=(A_1,\ldots, A_k)\in B({\mathcal H})^{n_1+\cdots + n_k}$ is a k-tuple of ![]() ${\mathcal U}$-commuting row operators and
${\mathcal U}$-commuting row operators and ![]() ${\mathcal U}'$ is the commutant
${\mathcal U}'$ is the commutant ![]() ${\mathcal U}$, then
${\mathcal U}$, then
 \begin{equation*}\Phi_{A_{i_1}}\circ\Phi_{A_{i_2}}\circ \cdots \circ\Phi_{A_{i_p}}(Y)=\Phi_{A_{i_{\sigma(1)}}}\circ\Phi_{A_{i_{\sigma(2)}}}\circ \cdots \circ\Phi_{A_{i_{\sigma(p)}}}(Y), \qquad Y\in {\mathcal U}',
\end{equation*}
\begin{equation*}\Phi_{A_{i_1}}\circ\Phi_{A_{i_2}}\circ \cdots \circ\Phi_{A_{i_p}}(Y)=\Phi_{A_{i_{\sigma(1)}}}\circ\Phi_{A_{i_{\sigma(2)}}}\circ \cdots \circ\Phi_{A_{i_{\sigma(p)}}}(Y), \qquad Y\in {\mathcal U}',
\end{equation*} for any ![]() $i_1,\ldots, i_p\in \{1,\ldots, k\}$ and any permutation σ of the set
$i_1,\ldots, i_p\in \{1,\ldots, k\}$ and any permutation σ of the set ![]() $\{1,\ldots, p\}$ and
$\{1,\ldots, p\}$ and
for any permutation ω of the set ![]() $\{1,\ldots, k\}$.
$\{1,\ldots, k\}$.
If, in addition, ![]() $Y=Y^*\in {\mathcal U}'$ is such that
$Y=Y^*\in {\mathcal U}'$ is such that ![]() $\Delta_A(Y)\geq0$, then the following statements hold:
$\Delta_A(Y)\geq0$, then the following statements hold:
(i) For any
 $q_1,\ldots, q_k\in {\mathbb N}$,
$q_1,\ldots, q_k\in {\mathbb N}$,
 \begin{equation*}
\begin{split}
0&\leq\sum_{p_k=0}^{q_k-1} \cdots \sum_{p_1=0}^{q_1-1}\Phi_{A_k}^{p_k}\circ\cdots\circ \Phi_{A_1}^{p_1} (\Delta_A(Y))
=(id-\Phi_{A_k}^{q_k})\circ\cdots \circ (id-\Phi_{A_1}^{q_1})(Y).
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
0&\leq\sum_{p_k=0}^{q_k-1} \cdots \sum_{p_1=0}^{q_1-1}\Phi_{A_k}^{p_k}\circ\cdots\circ \Phi_{A_1}^{p_1} (\Delta_A(Y))
=(id-\Phi_{A_k}^{q_k})\circ\cdots \circ (id-\Phi_{A_1}^{q_1})(Y).
\end{split}
\end{equation*}(ii) If each Ai is pure, i.e.
 $\Phi_{A_i}^m(I)\to 0$ weakly as
$\Phi_{A_i}^m(I)\to 0$ weakly as  $m\to\infty$, then
$m\to\infty$, then  $Y\geq 0$,
$Y\geq 0$,
 \begin{equation*}
Y=\sum_{p_k=0}^{\infty} \cdots \sum_{p_1=0}^{\infty}\Phi_{A_k}^{p_k}\circ\cdots\circ \Phi_{A_1}^{p_1} (\Delta_A(Y))
\end{equation*}
\begin{equation*}
Y=\sum_{p_k=0}^{\infty} \cdots \sum_{p_1=0}^{\infty}\Phi_{A_k}^{p_k}\circ\cdots\circ \Phi_{A_1}^{p_1} (\Delta_A(Y))
\end{equation*}and
 \begin{equation*}(id-\Phi_{A_1})^{s_1}\circ\cdots \circ (id-\Phi_{A_k})^{s_k}(Y)\geq 0\quad \text{for any }\ s_1,\ldots, s_k\in \{0,1\}
\end{equation*}
\begin{equation*}(id-\Phi_{A_1})^{s_1}\circ\cdots \circ (id-\Phi_{A_k})^{s_k}(Y)\geq 0\quad \text{for any }\ s_1,\ldots, s_k\in \{0,1\}
\end{equation*}
Proof. Since ![]() $A_{i,s} $ is in the commutant of
$A_{i,s} $ is in the commutant of ![]() ${\mathcal U}$ which is a set consisting of unitary operators, it is clear that
${\mathcal U}$ which is a set consisting of unitary operators, it is clear that ![]() $A_{i,s} $ is in the commutant of
$A_{i,s} $ is in the commutant of ![]() ${\mathcal U}^*$. Consequently, using the fact that
${\mathcal U}^*$. Consequently, using the fact that ![]() $
A_{i,s} A_{j,t}=U_{i,j}(s,t)A_{j,t}A_{i,s}$ for
$
A_{i,s} A_{j,t}=U_{i,j}(s,t)A_{j,t}A_{i,s}$ for ![]() $ (i,j,s,t)\in \Gamma$, we deduce that
$ (i,j,s,t)\in \Gamma$, we deduce that
 \begin{equation*}
\begin{split}
\Phi_{A_i} \circ\Phi_{A_j}(Y)&= \sum_{s=1}^{n_i} \sum_{t=1}^{n_j} A_{i,s} A_{j,t} YA_{j,t}^* A_{i,s}^*\\
&= \sum_{t=1}^{n_j}\sum_{s=1}^{n_i} U_{i,j}(s,t) A_{j,t}A_{i,s}YA_{i,s}^*A_{j,t}^* U_{i,j}(s,t)^*\\
&=\Phi_{A_j}\circ\Phi_{A_i}(Y)
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
\Phi_{A_i} \circ\Phi_{A_j}(Y)&= \sum_{s=1}^{n_i} \sum_{t=1}^{n_j} A_{i,s} A_{j,t} YA_{j,t}^* A_{i,s}^*\\
&= \sum_{t=1}^{n_j}\sum_{s=1}^{n_i} U_{i,j}(s,t) A_{j,t}A_{i,s}YA_{i,s}^*A_{j,t}^* U_{i,j}(s,t)^*\\
&=\Phi_{A_j}\circ\Phi_{A_i}(Y)
\end{split}
\end{equation*} for any ![]() $Y\in {\mathcal U}'$ and
$Y\in {\mathcal U}'$ and ![]() $i,j\in \{1,\ldots, k\}$. Using this argument repeatedly, one can easily prove the first part of the proposition.
$i,j\in \{1,\ldots, k\}$. Using this argument repeatedly, one can easily prove the first part of the proposition.
Now, assume that ![]() $Y=Y^*\in {\mathcal U}'$ and
$Y=Y^*\in {\mathcal U}'$ and ![]() $\Delta_A(Y)\geq0$. Since
$\Delta_A(Y)\geq0$. Since ![]() $A_{i,s}\in {\mathcal U}'$, we also have
$A_{i,s}\in {\mathcal U}'$, we also have ![]() $\Delta_A(Y)\in {\mathcal U}'$. Due to the first part of this proposition and the fact that
$\Delta_A(Y)\in {\mathcal U}'$. Due to the first part of this proposition and the fact that ![]() $\Delta_{A}(Y):=(id-\Phi_{A_1})\circ\cdots \circ(id-\Phi_{A_k})(Y)\geq 0,$ item (i) follows immediately. To prove item (ii), assume that each Ai is pure, i.e.
$\Delta_{A}(Y):=(id-\Phi_{A_1})\circ\cdots \circ(id-\Phi_{A_k})(Y)\geq 0,$ item (i) follows immediately. To prove item (ii), assume that each Ai is pure, i.e.  $\Phi_{A_i}^m(I)\to 0$ weakly as
$\Phi_{A_i}^m(I)\to 0$ weakly as ![]() $m\to\infty$. Note that if
$m\to\infty$. Note that if ![]() $X=X^*\in B({\mathcal H})$, then
$X=X^*\in B({\mathcal H})$, then
 \begin{equation*}
-\|X\|\Phi_{A_i}^m(I)\leq \Phi_{A_i}^m(X)\leq \|X\|\Phi_{A_i}^m(I).\end{equation*}
\begin{equation*}
-\|X\|\Phi_{A_i}^m(I)\leq \Phi_{A_i}^m(X)\leq \|X\|\Phi_{A_i}^m(I).\end{equation*} Hence,  $\Phi_{A_i}^m(X)\to 0$ weakly as
$\Phi_{A_i}^m(X)\to 0$ weakly as ![]() $m\to\infty$. Using this fact repeatedly in item (i), we conclude that
$m\to\infty$. Using this fact repeatedly in item (i), we conclude that
 \begin{equation*}
0\leq Y=\sum_{p_k=0}^{\infty} \cdots \sum_{p_1=0}^{\infty}\Phi_{A_k}^{p_k}\circ\cdots\circ \Phi_{A_1}^{p_1} (\Delta_A(Y)),
\end{equation*}
\begin{equation*}
0\leq Y=\sum_{p_k=0}^{\infty} \cdots \sum_{p_1=0}^{\infty}\Phi_{A_k}^{p_k}\circ\cdots\circ \Phi_{A_1}^{p_1} (\Delta_A(Y)),
\end{equation*} where the convergence is in the weak operator topology. Since ![]() $\Delta_{A}(Y)\geq 0$ and
$\Delta_{A}(Y)\geq 0$ and ![]() $Y\geq 0$, we deduce that
$Y\geq 0$, we deduce that ![]() $\Phi_{A_1}(\Delta_{(A_2,\ldots, A_k)}(Y))\leq \Delta_{(A_2,\ldots, A_k)}(Y)$, where
$\Phi_{A_1}(\Delta_{(A_2,\ldots, A_k)}(Y))\leq \Delta_{(A_2,\ldots, A_k)}(Y)$, where ![]() $\Delta_{(A_2,\ldots, A_k)}(Y):=(id-\Phi_{A_2})\circ\cdots \circ(id-\Phi_{A_k})(Y)$ is a self-adjoint operator. Hence,
$\Delta_{(A_2,\ldots, A_k)}(Y):=(id-\Phi_{A_2})\circ\cdots \circ(id-\Phi_{A_k})(Y)$ is a self-adjoint operator. Hence,  $\Phi_{A_1}^m(\Delta_{(A_2,\ldots, A_k)}(Y))\leq \Delta_{(A_2,\ldots, A_k)}(Y)$ for any
$\Phi_{A_1}^m(\Delta_{(A_2,\ldots, A_k)}(Y))\leq \Delta_{(A_2,\ldots, A_k)}(Y)$ for any ![]() $m\in {\mathbb N}$ and
$m\in {\mathbb N}$ and
 \begin{equation*}
-\|\Delta_{(A_2,\ldots, A_k)}(Y)\| \Phi_{A_1}^m(I)\leq \Phi_{A_1}^m(\Delta_{(A_2,\ldots, A_k)}(Y))
\leq \|\Delta_{(A_2,\ldots, A_k)}(Y)\| \Phi_{A_1}^m(I)
\end{equation*}
\begin{equation*}
-\|\Delta_{(A_2,\ldots, A_k)}(Y)\| \Phi_{A_1}^m(I)\leq \Phi_{A_1}^m(\Delta_{(A_2,\ldots, A_k)}(Y))
\leq \|\Delta_{(A_2,\ldots, A_k)}(Y)\| \Phi_{A_1}^m(I)
\end{equation*} for any ![]() $m\in {\mathbb N}$. Taking
$m\in {\mathbb N}$. Taking ![]() $m\to \infty$ and using the fact that
$m\to \infty$ and using the fact that  $\Phi_{A_1}^m(I)\to 0$ weakly as
$\Phi_{A_1}^m(I)\to 0$ weakly as ![]() $m\to\infty$, we conclude that
$m\to\infty$, we conclude that ![]() $\Delta_{(A_2,\ldots, A_k)}(Y)\geq 0$. Using similar arguments and the first part of the proposition, we can deduce that
$\Delta_{(A_2,\ldots, A_k)}(Y)\geq 0$. Using similar arguments and the first part of the proposition, we can deduce that ![]() $(id-\Phi_{A_1})^{p_1}\circ \cdots \circ (id-\Phi_{A_k})^{p_k}(Y)\geq 0$ for any
$(id-\Phi_{A_1})^{p_1}\circ \cdots \circ (id-\Phi_{A_k})^{p_k}(Y)\geq 0$ for any ![]() $p_i\in \{0,1\}$.
$p_i\in \{0,1\}$.
Let ![]() $A:=(A_1,\ldots, A_k)\in B({\mathcal H})^{n_1+\cdots+ n_k} $ with
$A:=(A_1,\ldots, A_k)\in B({\mathcal H})^{n_1+\cdots+ n_k} $ with ![]() $A_i:=[A_{i,1}\cdots A_{i,n_i}]$. We say that Ai is row power bounded if there is M > 0 such that
$A_i:=[A_{i,1}\cdots A_{i,n_i}]$. We say that Ai is row power bounded if there is M > 0 such that  $\|\Phi_{A_i}^m(I)\|\leq M$ for any
$\|\Phi_{A_i}^m(I)\|\leq M$ for any ![]() $m\in {\mathbb N}$.
$m\in {\mathbb N}$.
Corollary. Let ![]() $A:=(A_1,\ldots, A_k)\in B({\mathcal H})^{n_1+\cdots + n_k}$ be a k-tuple of
$A:=(A_1,\ldots, A_k)\in B({\mathcal H})^{n_1+\cdots + n_k}$ be a k-tuple of ![]() ${\mathcal U}$-commuting row operators.
${\mathcal U}$-commuting row operators.
(i) If
 $\Delta_A(I)\geq0$ and each Ai is a pure tuple, then A is in the regular
$\Delta_A(I)\geq0$ and each Ai is a pure tuple, then A is in the regular  ${\mathcal U}$-twisted polyball
${\mathcal U}$-twisted polyball  $\textbf{B}^{\mathcal U}_{reg}({\mathcal H})$ and
$\textbf{B}^{\mathcal U}_{reg}({\mathcal H})$ and
 \begin{equation*}\sum_{p_k=0}^{\infty} \cdots \sum_{p_1=0}^{\infty}\Phi_{A_k}^{p_k}\circ\cdots\circ \Phi_{A_1}^{p_1} (\Delta_A(I))=I.
\end{equation*}
\begin{equation*}\sum_{p_k=0}^{\infty} \cdots \sum_{p_1=0}^{\infty}\Phi_{A_k}^{p_k}\circ\cdots\circ \Phi_{A_1}^{p_1} (\Delta_A(I))=I.
\end{equation*}(ii) If
 $\Delta_{rA}(I)\geq0$ for any
$\Delta_{rA}(I)\geq0$ for any  $r\in [0,1)$ and each Ai is a row power bounded tuple, then A is in the regular
$r\in [0,1)$ and each Ai is a row power bounded tuple, then A is in the regular  ${\mathcal U}$-twisted polyball.
${\mathcal U}$-twisted polyball.
Proof. Part (i) follows from proposition 2.3, part (ii), in the particular case when Y = I. To prove item (ii), we note that since Ai is power bounded, rAi is pure for any ![]() $r\in [0,1)$. Applying proposition 2.3 part (ii) to rA, we deduce that
$r\in [0,1)$. Applying proposition 2.3 part (ii) to rA, we deduce that
Hence, each Ai is a row contraction and A is in the regular ![]() ${\mathcal U}$-twisted polyball. This completes the proof.
${\mathcal U}$-twisted polyball. This completes the proof.
Given two k-tuples ![]() $\textbf{q}=(q_1,\ldots, q_k)$ and
$\textbf{q}=(q_1,\ldots, q_k)$ and ![]() $\textbf{p}=(p_1,\ldots, p_k)$ in
$\textbf{p}=(p_1,\ldots, p_k)$ in  ${\mathbb Z}_+^k$, where
${\mathbb Z}_+^k$, where ![]() ${\mathbb Z}_+:=\{0,1,\ldots\}$, we set
${\mathbb Z}_+:=\{0,1,\ldots\}$, we set ![]() $\textbf{q}\leq \textbf{p}$ if
$\textbf{q}\leq \textbf{p}$ if ![]() $q_i\leq p_i$ for any
$q_i\leq p_i$ for any ![]() $i\in \{1,\ldots, k\}$. We consider
$i\in \{1,\ldots, k\}$. We consider  ${\mathbb Z}_+^k$ as a directed set with respect to this partial order.
${\mathbb Z}_+^k$ as a directed set with respect to this partial order.
Theorem 2.5 Let ![]() $A:=(A_1,\ldots, A_k)\in B({\mathcal H})^{n_1+\cdots + n_k}$ with
$A:=(A_1,\ldots, A_k)\in B({\mathcal H})^{n_1+\cdots + n_k}$ with ![]() $A_i:=(A_{i,1},\ldots, A_{i,n_i})$ be a k-tuple of
$A_i:=(A_{i,1},\ldots, A_{i,n_i})$ be a k-tuple of ![]() ${\mathcal U}$-commuting operators, and let
${\mathcal U}$-commuting operators, and let ![]() $\Phi_{A_i}$ and
$\Phi_{A_i}$ and  $\Phi_{A_i}^*$ be the completely positive linear maps on
$\Phi_{A_i}^*$ be the completely positive linear maps on ![]() $B({\mathcal H})$ defined by
$B({\mathcal H})$ defined by
 \begin{equation*}
\Phi_{A_i}(X):=\sum_{j=1}^{n_i} A_iXA_i^* \quad \text{and }\quad \Phi^*_{A_i}(X):=\sum_{j=1}^{n_i} A^*_iXA_i.
\end{equation*}
\begin{equation*}
\Phi_{A_i}(X):=\sum_{j=1}^{n_i} A_iXA_i^* \quad \text{and }\quad \Phi^*_{A_i}(X):=\sum_{j=1}^{n_i} A^*_iXA_i.
\end{equation*} If ![]() $\Delta_A(I)$ is a positive trace class operator and
$\Delta_A(I)$ is a positive trace class operator and  $M_i\geq \|\Phi^*_{A_i}(I)\| \gt 0$, then the limit
$M_i\geq \|\Phi^*_{A_i}(I)\| \gt 0$, then the limit
 \begin{equation*}
\lim_{m\to\infty}\frac{1}{\left(\begin{matrix} m+k-1\\ k-1\end{matrix}\right)}\sum_{{q_1\geq 0,\ldots, q_k\geq 0}\atop {q_1+\cdots +q_k=m}} \frac{1}{M_1^{q_1}\cdots M_k^{q_k}}
\mathrm{trace\,}\left[ \Phi_{A_1}^{q_1}\circ \cdots \circ \Phi_{A_k}^{q_k}(\Delta_A(I))\right]
\end{equation*}
\begin{equation*}
\lim_{m\to\infty}\frac{1}{\left(\begin{matrix} m+k-1\\ k-1\end{matrix}\right)}\sum_{{q_1\geq 0,\ldots, q_k\geq 0}\atop {q_1+\cdots +q_k=m}} \frac{1}{M_1^{q_1}\cdots M_k^{q_k}}
\mathrm{trace\,}\left[ \Phi_{A_1}^{q_1}\circ \cdots \circ \Phi_{A_k}^{q_k}(\Delta_A(I))\right]
\end{equation*} exists and is bounded above by ![]() $\mathrm{trace\,}[\Delta_A(I)]$.
$\mathrm{trace\,}[\Delta_A(I)]$.
Proof. If ![]() $Y\geq 0$ is a trace class operator, then
$Y\geq 0$ is a trace class operator, then
 \begin{equation*}
\begin{split}
\mathrm{trace\,} [\Phi_{A_i}(Y)]&=\sum_{j=1}^{n_i} \mathrm{trace\,} (A_{i,j}YA_{i,j}^*)
= \mathrm{trace\,} \left[ \left(\sum_{j=1}^{n_i}A_{i,j}^*A_{i,j}\right)Y\right]\\
&\leq \|\Phi^*_{A_i}(I)\| \mathrm{trace\,} Y\leq M_i\mathrm{trace\,} Y
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
\mathrm{trace\,} [\Phi_{A_i}(Y)]&=\sum_{j=1}^{n_i} \mathrm{trace\,} (A_{i,j}YA_{i,j}^*)
= \mathrm{trace\,} \left[ \left(\sum_{j=1}^{n_i}A_{i,j}^*A_{i,j}\right)Y\right]\\
&\leq \|\Phi^*_{A_i}(I)\| \mathrm{trace\,} Y\leq M_i\mathrm{trace\,} Y
\end{split}
\end{equation*} for any ![]() $i\in \{1,\ldots, k\}$. Hence,
$i\in \{1,\ldots, k\}$. Hence,  $
\frac{1}{M_i} \mathrm{trace\,} [\Phi_{A_i}(Y)]\leq \mathrm{trace\,} Y$ for any
$
\frac{1}{M_i} \mathrm{trace\,} [\Phi_{A_i}(Y)]\leq \mathrm{trace\,} Y$ for any ![]() $i\in \{1,\ldots, k\}$. Consequently, since
$i\in \{1,\ldots, k\}$. Consequently, since ![]() $\Delta_A(I)$ is a positive trace class operator and A is a
$\Delta_A(I)$ is a positive trace class operator and A is a ![]() ${\mathcal U}$-commuting tuple of operators,
${\mathcal U}$-commuting tuple of operators, ![]() $\Delta_A(I)\in {\mathcal U}'$ and we can use proposition 2.3 to deduce that the multi-sequence
$\Delta_A(I)\in {\mathcal U}'$ and we can use proposition 2.3 to deduce that the multi-sequence
 \begin{equation*}
\begin{split}
s_{q_1,\ldots,q_k}&:= \frac{1}{M_1^{q_1}\cdots M_k^{q_k}}
\mathrm{trace\,}\left[ \Phi_{A_1}^{q_1}\circ \cdots \circ \Phi_{A_k}^{q_k}(\Delta_A(I))\right]\\
&=
\frac{1}{M_{\sigma(1)}^{q_1}\cdots M_{\sigma(k)}^{q_k}}
\mathrm{trace\,}\left[ \Phi_{A_{\sigma(1)}}^{q_1}\circ \cdots \circ \Phi_{A_{\sigma(k)}}^{q_k}(\Delta_A(I))\right]
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
s_{q_1,\ldots,q_k}&:= \frac{1}{M_1^{q_1}\cdots M_k^{q_k}}
\mathrm{trace\,}\left[ \Phi_{A_1}^{q_1}\circ \cdots \circ \Phi_{A_k}^{q_k}(\Delta_A(I))\right]\\
&=
\frac{1}{M_{\sigma(1)}^{q_1}\cdots M_{\sigma(k)}^{q_k}}
\mathrm{trace\,}\left[ \Phi_{A_{\sigma(1)}}^{q_1}\circ \cdots \circ \Phi_{A_{\sigma(k)}}^{q_k}(\Delta_A(I))\right]
\end{split}
\end{equation*} is decreasing with respect to each of the indices ![]() $q_1,\ldots, q_k$ and
$q_1,\ldots, q_k$ and ![]() $s_{q_1,\ldots,q_k}\leq \mathrm{trace\,}(\Delta_A(I))$. Now, it is easy to see that
$s_{q_1,\ldots,q_k}\leq \mathrm{trace\,}(\Delta_A(I))$. Now, it is easy to see that
 \begin{equation*}
\lim_{q_1\to\infty}\cdots\lim_{q_k\to\infty} s_{q_1,\ldots,q_k}
= \lim_{(q_1,\ldots, q_k)\in {\mathbb Z}_+^k} s_{q_1,\ldots,q_k}=\inf_{(q_1,\ldots, q_k)\in {\mathbb Z}_+^k} s_{q_1,\ldots,q_k}\leq \mathrm{trace\,}(\Delta_A(I)).
\end{equation*}
\begin{equation*}
\lim_{q_1\to\infty}\cdots\lim_{q_k\to\infty} s_{q_1,\ldots,q_k}
= \lim_{(q_1,\ldots, q_k)\in {\mathbb Z}_+^k} s_{q_1,\ldots,q_k}=\inf_{(q_1,\ldots, q_k)\in {\mathbb Z}_+^k} s_{q_1,\ldots,q_k}\leq \mathrm{trace\,}(\Delta_A(I)).
\end{equation*} For each ![]() $\ell\in {\mathbb Z}_+$, denote
$\ell\in {\mathbb Z}_+$, denote
 \begin{equation*}
\Omega_\ell:=\{(q_1,\ldots,q_k)\in {\mathbb Z}_+^k:\ q_1+\cdots + q_k=m \text{ and } q_1\geq \ell,\ldots, q_k\geq\ell\}.
\end{equation*}
\begin{equation*}
\Omega_\ell:=\{(q_1,\ldots,q_k)\in {\mathbb Z}_+^k:\ q_1+\cdots + q_k=m \text{ and } q_1\geq \ell,\ldots, q_k\geq\ell\}.
\end{equation*} It is easy to see that  $$\mathrm{card}\,\Omega_0=\left(\begin{matrix} m+k-1\\ k-1\end{matrix}\right)$$ and
$$\mathrm{card}\,\Omega_0=\left(\begin{matrix} m+k-1\\ k-1\end{matrix}\right)$$ and  $$
\mathrm{card}\,(\Omega\backslash \Omega_\ell)\leq k\ell \left(\begin{matrix} m+k-2\\ k-1\end{matrix}\right)$$ for
$$
\mathrm{card}\,(\Omega\backslash \Omega_\ell)\leq k\ell \left(\begin{matrix} m+k-2\\ k-1\end{matrix}\right)$$ for ![]() $\ell\in {\mathbb Z}_+$. Set
$\ell\in {\mathbb Z}_+$. Set  $y:= \inf_{(q_1,\ldots, q_k)\in {\mathbb Z}_+^k} s_{q_1,\ldots,q_k}$, and let ϵ > 0. Then, there exists
$y:= \inf_{(q_1,\ldots, q_k)\in {\mathbb Z}_+^k} s_{q_1,\ldots,q_k}$, and let ϵ > 0. Then, there exists ![]() $p\in {\mathbb N}$,
$p\in {\mathbb N}$, ![]() $p\geq 1$, such that
$p\geq 1$, such that ![]() $|s_{q_1,\ldots,q_k}-y| \lt \epsilon$ for any
$|s_{q_1,\ldots,q_k}-y| \lt \epsilon$ for any ![]() $q_1\geq p,\ldots, q_k\geq p$. Consequently, we deduce that
$q_1\geq p,\ldots, q_k\geq p$. Consequently, we deduce that
 \begin{equation*}
\begin{split}
&\left| \frac{1}{\left(\begin{matrix} m+k-1\\ k-1\end{matrix}\right)}\sum_{{q_1\geq 0,\ldots, q_k\geq 0}\atop {q_1+\cdots +q_k=m}}s_{q_1,\ldots,q_k}-y\right|
=
\left| \frac{1}{\left(\begin{matrix} m+k-1\\ k-1\end{matrix}\right)}\sum_{{q_1\geq 0,\ldots, q_k\geq 0}\atop {q_1+\cdots +q_k=m}}(s_{q_1,\ldots,q_k}-y)\right|\\
&\leq\!
\frac{1}{\left(\begin{matrix} m+k-1\\ k-1\end{matrix}\right)}\!\sum_{(q_1,\ldots, q_k)\in \Omega_0\backslash\Omega_p }\!\!|s_{q_1,\ldots,q_k}-y|
\!+\! \frac{1}{\left(\begin{matrix} m+k-1\\ k-1\end{matrix}\right)}\sum_{(q_1,\ldots, q_k)\in \Omega_p }\!\!|s_{q_1,\ldots,q_k}-y|\\
&\leq
\frac{1}{\left(\begin{matrix} m+k-1\\ k-1\end{matrix}\right)} kp \left(\begin{matrix} m+k-2\\ k-2\end{matrix}\right) \left[\mathrm{trace\,}(\Delta_A(I) +y\right] +\epsilon.
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
&\left| \frac{1}{\left(\begin{matrix} m+k-1\\ k-1\end{matrix}\right)}\sum_{{q_1\geq 0,\ldots, q_k\geq 0}\atop {q_1+\cdots +q_k=m}}s_{q_1,\ldots,q_k}-y\right|
=
\left| \frac{1}{\left(\begin{matrix} m+k-1\\ k-1\end{matrix}\right)}\sum_{{q_1\geq 0,\ldots, q_k\geq 0}\atop {q_1+\cdots +q_k=m}}(s_{q_1,\ldots,q_k}-y)\right|\\
&\leq\!
\frac{1}{\left(\begin{matrix} m+k-1\\ k-1\end{matrix}\right)}\!\sum_{(q_1,\ldots, q_k)\in \Omega_0\backslash\Omega_p }\!\!|s_{q_1,\ldots,q_k}-y|
\!+\! \frac{1}{\left(\begin{matrix} m+k-1\\ k-1\end{matrix}\right)}\sum_{(q_1,\ldots, q_k)\in \Omega_p }\!\!|s_{q_1,\ldots,q_k}-y|\\
&\leq
\frac{1}{\left(\begin{matrix} m+k-1\\ k-1\end{matrix}\right)} kp \left(\begin{matrix} m+k-2\\ k-2\end{matrix}\right) \left[\mathrm{trace\,}(\Delta_A(I) +y\right] +\epsilon.
\end{split}
\end{equation*} Taking ![]() $m\to \infty$, we deduce that
$m\to \infty$, we deduce that
 \begin{equation*}
\lim_{m\to\infty} \frac{1}{\left(\begin{matrix} m+k-1\\ k-1\end{matrix}\right)}\sum_{{q_1\geq 0,\ldots, q_k\geq 0}\atop {q_1+\cdots +q_k=m}}s_{q_1,\ldots,q_k}=y.
\end{equation*}
\begin{equation*}
\lim_{m\to\infty} \frac{1}{\left(\begin{matrix} m+k-1\\ k-1\end{matrix}\right)}\sum_{{q_1\geq 0,\ldots, q_k\geq 0}\atop {q_1+\cdots +q_k=m}}s_{q_1,\ldots,q_k}=y.
\end{equation*}This completes the proof.
Corollary 2.6. The limit in theorem 2.5 is equal to
 \begin{equation*}
\begin{split}
&\lim_{m\to\infty}\frac{1}{\left(\begin{matrix} m+k\\ k\end{matrix}\right)}\sum_{{q_1\geq 0,\ldots, q_k\geq 0}\atop {q_1+\cdots +q_k\leq m}} \frac{1}{M_1^{q_1}\cdots M_k^{q_k}}
\mathrm{trace\,}\left[ \Phi_{A_1}^{q_1}\circ \cdots \circ \Phi_{A_k}^{q_k}(\Delta_A(I))\right]
\\ &=
\lim_{q_1\to\infty}\cdots\lim_{q_k\to\infty} \frac{1}{M_{\sigma(1)}^{q_1}\cdots M_{\sigma(k)}^{q_k}} \mathrm{trace\,}\left[ \Phi_{A_{\sigma(1)}}^{q_1}\circ \cdots \circ \Phi_{A_{\sigma(k)}}^{q_k}(\Delta_A(I))\right]\\
&= \lim_{q_1\to\infty}\cdots\lim_{q_k\to\infty} \frac{1}{q_1}\sum_{s_1=0}^{q_1}\cdots \frac{1}{q_k}\sum_{s_k=0}^{q_k} \frac{1}{M_{\sigma(1)}^{s_1}\cdots M_{\sigma(k)}^{s_k}}
\mathrm{trace\,}\\
&\qquad\left[ \Phi_{A_{\sigma(1)}}^{s_1}\circ \cdots \circ \Phi_{A_{\sigma(k)}}^{s_k}(\Delta_A(I))\right]
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
&\lim_{m\to\infty}\frac{1}{\left(\begin{matrix} m+k\\ k\end{matrix}\right)}\sum_{{q_1\geq 0,\ldots, q_k\geq 0}\atop {q_1+\cdots +q_k\leq m}} \frac{1}{M_1^{q_1}\cdots M_k^{q_k}}
\mathrm{trace\,}\left[ \Phi_{A_1}^{q_1}\circ \cdots \circ \Phi_{A_k}^{q_k}(\Delta_A(I))\right]
\\ &=
\lim_{q_1\to\infty}\cdots\lim_{q_k\to\infty} \frac{1}{M_{\sigma(1)}^{q_1}\cdots M_{\sigma(k)}^{q_k}} \mathrm{trace\,}\left[ \Phi_{A_{\sigma(1)}}^{q_1}\circ \cdots \circ \Phi_{A_{\sigma(k)}}^{q_k}(\Delta_A(I))\right]\\
&= \lim_{q_1\to\infty}\cdots\lim_{q_k\to\infty} \frac{1}{q_1}\sum_{s_1=0}^{q_1}\cdots \frac{1}{q_k}\sum_{s_k=0}^{q_k} \frac{1}{M_{\sigma(1)}^{s_1}\cdots M_{\sigma(k)}^{s_k}}
\mathrm{trace\,}\\
&\qquad\left[ \Phi_{A_{\sigma(1)}}^{s_1}\circ \cdots \circ \Phi_{A_{\sigma(k)}}^{s_k}(\Delta_A(I))\right]
\end{split}
\end{equation*} for any permutation σ of the set ![]() $\{1,\ldots, k\}$.
$\{1,\ldots, k\}$.
Proof. Setting  $a_m:=\sum_{{q_1\geq 0,\ldots, q_k\geq 0}\atop {q_1+\cdots +q_k=m}} \frac{1}{M_1^{q_1}\cdots M_k^{q_k}}
\mathrm{trace\,}\left[ \Phi_{A_1}^{q_1}\circ \cdots \circ \Phi_{A_k}^{q_k}(\Delta_A(I))\right]$ and
$a_m:=\sum_{{q_1\geq 0,\ldots, q_k\geq 0}\atop {q_1+\cdots +q_k=m}} \frac{1}{M_1^{q_1}\cdots M_k^{q_k}}
\mathrm{trace\,}\left[ \Phi_{A_1}^{q_1}\circ \cdots \circ \Phi_{A_k}^{q_k}(\Delta_A(I))\right]$ and  $$b_m= \left(\begin{matrix} m+k-1\\ k-1\end{matrix}\right)$$, and taking into account that
$$b_m= \left(\begin{matrix} m+k-1\\ k-1\end{matrix}\right)$$, and taking into account that
 \begin{equation*}
\left(\begin{matrix} k-1\\ k-1\end{matrix}\right)+ \left(\begin{matrix} k\\ k-1\end{matrix}\right)+\cdots + \left(\begin{matrix} m+k-1\\ k-1\end{matrix}\right)= \left(\begin{matrix} m+k\\ k\end{matrix}\right),
\end{equation*}
\begin{equation*}
\left(\begin{matrix} k-1\\ k-1\end{matrix}\right)+ \left(\begin{matrix} k\\ k-1\end{matrix}\right)+\cdots + \left(\begin{matrix} m+k-1\\ k-1\end{matrix}\right)= \left(\begin{matrix} m+k\\ k\end{matrix}\right),
\end{equation*}we have
 \begin{align*}
\frac{a_0+a_1+\cdots + a_m}{b_0+b_1+\cdots +b_m}=& \frac{1}{\left(\begin{matrix} m+k\\ k\end{matrix}\right)}\sum_{{q_1\geq 0,\ldots, q_k\geq 0}\atop {q_1+\cdots +q_k\leq m}} \frac{1}{M_1^{q_1}\cdots M_k^{q_k}}\\
&\qquad\mathrm{trace\,}\left[\Phi_{A_1}^{q_1}\circ \cdots \circ \Phi_{A_k}^{q_k}(\Delta_A(I))\right].
\end{align*}
\begin{align*}
\frac{a_0+a_1+\cdots + a_m}{b_0+b_1+\cdots +b_m}=& \frac{1}{\left(\begin{matrix} m+k\\ k\end{matrix}\right)}\sum_{{q_1\geq 0,\ldots, q_k\geq 0}\atop {q_1+\cdots +q_k\leq m}} \frac{1}{M_1^{q_1}\cdots M_k^{q_k}}\\
&\qquad\mathrm{trace\,}\left[\Phi_{A_1}^{q_1}\circ \cdots \circ \Phi_{A_k}^{q_k}(\Delta_A(I))\right].
\end{align*} Due to theorem 2.5, ![]() $\lim_{m\to\infty}\frac{a_m}{b_m}$ exists. Consequently, denoting by y the limit in theorem 2.5 and using Stolz–Cesáro convergence theorem, we deduce that
$\lim_{m\to\infty}\frac{a_m}{b_m}$ exists. Consequently, denoting by y the limit in theorem 2.5 and using Stolz–Cesáro convergence theorem, we deduce that
 \begin{equation*}
\lim_{m\to\infty}\frac{1}{\left(\begin{matrix} m+k\\ k\end{matrix}\right)}\sum_{{q_1\geq 0,\ldots, q_k\geq 0}\atop {q_1+\cdots +q_k\leq m}} \frac{1}{M_1^{q_1}\cdots M_k^{q_k}}
\mathrm{trace\,}\left[ \Phi_{A_1}^{q_1}\circ \cdots \circ \Phi_{A_k}^{q_k}(\Delta_A(I))\right]=y.
\end{equation*}
\begin{equation*}
\lim_{m\to\infty}\frac{1}{\left(\begin{matrix} m+k\\ k\end{matrix}\right)}\sum_{{q_1\geq 0,\ldots, q_k\geq 0}\atop {q_1+\cdots +q_k\leq m}} \frac{1}{M_1^{q_1}\cdots M_k^{q_k}}
\mathrm{trace\,}\left[ \Phi_{A_1}^{q_1}\circ \cdots \circ \Phi_{A_k}^{q_k}(\Delta_A(I))\right]=y.
\end{equation*}According to the proof of theorem 2.5, we also have
 \begin{equation*}y=\lim_{q_1\to\infty}\cdots\lim_{q_k\to\infty}\frac{1}{M_{\sigma(1)}^{q_1}\cdots M_{\sigma(k)}^{q_k}}
\mathrm{trace\,}\left[ \Phi_{A_{\sigma(1)}}^{q_1}\circ \cdots \circ \Phi_{A_{\sigma(k)}}^{q_k}(\Delta_A(I))\right].
\end{equation*}
\begin{equation*}y=\lim_{q_1\to\infty}\cdots\lim_{q_k\to\infty}\frac{1}{M_{\sigma(1)}^{q_1}\cdots M_{\sigma(k)}^{q_k}}
\mathrm{trace\,}\left[ \Phi_{A_{\sigma(1)}}^{q_1}\circ \cdots \circ \Phi_{A_{\sigma(k)}}^{q_k}(\Delta_A(I))\right].
\end{equation*}The last equality in the corollary follows after a repeated application of the Stolz-Cesásro convergence theorem. We leave it to the reader.
Let ![]() $A:=(A_1,\ldots, A_k)\in B({\mathcal H})^{n_1+\cdots + n_k}$ with
$A:=(A_1,\ldots, A_k)\in B({\mathcal H})^{n_1+\cdots + n_k}$ with ![]() $A_i:=(A_{i,1},\ldots, A_{i,n_i})$ be a k-tuple of
$A_i:=(A_{i,1},\ldots, A_{i,n_i})$ be a k-tuple of ![]() ${\mathcal U}$-commuting operators and let
${\mathcal U}$-commuting operators and let ![]() $\Phi_{A_i}$ and
$\Phi_{A_i}$ and  $\Phi_{A_i}^*$ be the completely positive linear maps on
$\Phi_{A_i}^*$ be the completely positive linear maps on ![]() $B({\mathcal H})$ defined by
$B({\mathcal H})$ defined by
 \begin{equation*}
\Phi_{A_i}(X):=\sum_{j=1}^{n_i} A_iXA_i^* \quad \text{and }\quad \Phi^*_{A_i}(X):=\sum_{j=1}^{n_i} A^*_iXA_i.
\end{equation*}
\begin{equation*}
\Phi_{A_i}(X):=\sum_{j=1}^{n_i} A_iXA_i^* \quad \text{and }\quad \Phi^*_{A_i}(X):=\sum_{j=1}^{n_i} A^*_iXA_i.
\end{equation*} Throughout this paper, we assume that the defect operator ![]() $\Delta_A(I)$ is a positive trace class operator and
$\Delta_A(I)$ is a positive trace class operator and ![]() $M:=(M_1,\ldots, M_k)$ is such that
$M:=(M_1,\ldots, M_k)$ is such that  $M_i\geq \|\Phi^*_{A_i}(I)\| \gt 0$.
$M_i\geq \|\Phi^*_{A_i}(I)\| \gt 0$.
Definition 2.7. The M-curvature of A is defined by the relation
 \begin{equation*}
\mathrm{curv}_M({A}):=
\lim_{m\to\infty}\frac{1}{\left(\begin{matrix} m+k\\ k\end{matrix}\right)}\sum_{{q_1\geq 0,\ldots, q_k\geq 0}\atop {q_1+\cdots +q_k\leq m}} \frac{1}{M_1^{q_1}\cdots M_k^{q_k}}
\mathrm{trace\,}\left[ \Phi_{A_1}^{q_1}\circ \cdots \circ \Phi_{A_k}^{q_k}(\Delta_A(I))\right].
\end{equation*}
\begin{equation*}
\mathrm{curv}_M({A}):=
\lim_{m\to\infty}\frac{1}{\left(\begin{matrix} m+k\\ k\end{matrix}\right)}\sum_{{q_1\geq 0,\ldots, q_k\geq 0}\atop {q_1+\cdots +q_k\leq m}} \frac{1}{M_1^{q_1}\cdots M_k^{q_k}}
\mathrm{trace\,}\left[ \Phi_{A_1}^{q_1}\circ \cdots \circ \Phi_{A_k}^{q_k}(\Delta_A(I))\right].
\end{equation*} If  $M_i=\|\Phi^*_{A_i}(I)\|$ for any
$M_i=\|\Phi^*_{A_i}(I)\|$ for any ![]() $i\in \{1,\ldots, k\}$, the corresponding M-curvature is called
$i\in \{1,\ldots, k\}$, the corresponding M-curvature is called ![]() $*$-curvature and we use the notation
$*$-curvature and we use the notation ![]() $\mathrm{curv}_*({A})$. We remark that if A belongs to the
$\mathrm{curv}_*({A})$. We remark that if A belongs to the ![]() ${\mathcal U}$-twisted polyball, then we can take
${\mathcal U}$-twisted polyball, then we can take ![]() $M_i=n_i$, in which case the corresponding M-curvature is called curvature and we denote it by
$M_i=n_i$, in which case the corresponding M-curvature is called curvature and we denote it by ![]() $\mathrm{curv}({A})$.
$\mathrm{curv}({A})$.
Corollary 2.8. Let ![]() $A:=(A_1,\ldots, A_k)$ be a k-tuple of
$A:=(A_1,\ldots, A_k)$ be a k-tuple of ![]() ${\mathcal U}$-commuting operators such that
${\mathcal U}$-commuting operators such that ![]() $\Delta_A(I)$ is a positive trace class operator. Then the following statements hold:
$\Delta_A(I)$ is a positive trace class operator. Then the following statements hold:
(i) For any
 $M:=(M_1,\ldots, M_k)$ such that
$M:=(M_1,\ldots, M_k)$ such that  $M_i\geq \|\Phi^*_{A_i}(I)\| \gt 0$,
$M_i\geq \|\Phi^*_{A_i}(I)\| \gt 0$,
 \begin{equation*}
0\leq \mathrm{curv}_M({A})\leq \mathrm{curv}_*({A})\leq \mathrm{trace\,}\left[{\Delta_{A}}(I)\right].
\end{equation*}
\begin{equation*}
0\leq \mathrm{curv}_M({A})\leq \mathrm{curv}_*({A})\leq \mathrm{trace\,}\left[{\Delta_{A}}(I)\right].
\end{equation*}(ii) If
 $\mathrm{curv}_*({A}) \gt 0$ and there is j such that
$\mathrm{curv}_*({A}) \gt 0$ and there is j such that  $M_j \gt \|\Phi^*_{A_j}(I)\|$, then
$M_j \gt \|\Phi^*_{A_j}(I)\|$, then
 \begin{equation*}\mathrm{curv}_{M}({A})=0.\end{equation*}
\begin{equation*}\mathrm{curv}_{M}({A})=0.\end{equation*}(iii) If A is in the
 ${\mathcal U}$-twisted polyball
${\mathcal U}$-twisted polyball  $\textbf{B}^{\mathcal U}({\mathcal H})$ and
$\textbf{B}^{\mathcal U}({\mathcal H})$ and  $ \mathrm{curv} (A) \gt 0$, then
$ \mathrm{curv} (A) \gt 0$, then
 \begin{equation*} \mathrm{curv}_*({A})= \mathrm{curv}({A})\quad \text{and }\quad \|\Phi^*_{A_i}(I)\|=n_i
\end{equation*}
\begin{equation*} \mathrm{curv}_*({A})= \mathrm{curv}({A})\quad \text{and }\quad \|\Phi^*_{A_i}(I)\|=n_i
\end{equation*}for any
 $i\in \{1,\ldots, k\}$.
$i\in \{1,\ldots, k\}$.(iv) If A is in the regular
 ${\mathcal U}$-twisted polyball
${\mathcal U}$-twisted polyball  $\textbf{B}^{\mathcal U}_{reg}({\mathcal H})$, then
$\textbf{B}^{\mathcal U}_{reg}({\mathcal H})$, then
 \begin{equation*} \mathrm{curv}_*({A})\leq \mathrm{trace\,}\left[{\Delta_{A}}(I)\right]\leq \mathrm{rank}\, [{\Delta_{A}}(I)].
\end{equation*}
\begin{equation*} \mathrm{curv}_*({A})\leq \mathrm{trace\,}\left[{\Delta_{A}}(I)\right]\leq \mathrm{rank}\, [{\Delta_{A}}(I)].
\end{equation*}
Proof. Using theorem 2.5, we obtain the inequalities in item (i). To prove (ii), assume that ![]() $\mathrm{curv}_*({A}) \gt 0$ and there is j such that
$\mathrm{curv}_*({A}) \gt 0$ and there is j such that  $M_j \gt \|\Phi^*_{A_j}(I)\|$. Suppose that
$M_j \gt \|\Phi^*_{A_j}(I)\|$. Suppose that ![]() $\mathrm{curv}_{M}({A}) \gt 0$. Since
$\mathrm{curv}_{M}({A}) \gt 0$. Since ![]() $\mathrm{curv}_*({A}) \lt \infty$, we have
$\mathrm{curv}_*({A}) \lt \infty$, we have  $\frac{\mathrm{curv}_*({A})}{\mathrm{curv}_{M}({A})} \lt \infty$. On the other hand, due to theorem 2.5 and corollary 2.6,
$\frac{\mathrm{curv}_*({A})}{\mathrm{curv}_{M}({A})} \lt \infty$. On the other hand, due to theorem 2.5 and corollary 2.6,
 \begin{equation*}\mathrm{curv}_M({A})=\lim_{q_1\to\infty}\cdots\lim_{q_k\to\infty} \frac{1}{M_1^{q_1}\cdots M_k^{q_k}}\mathrm{trace\,}\left[ \Phi_{A_1}^{q_1}\circ \cdots \circ \Phi_{A_k}^{q_k}({\Delta_{A}}(I))\right].
\end{equation*}
\begin{equation*}\mathrm{curv}_M({A})=\lim_{q_1\to\infty}\cdots\lim_{q_k\to\infty} \frac{1}{M_1^{q_1}\cdots M_k^{q_k}}\mathrm{trace\,}\left[ \Phi_{A_1}^{q_1}\circ \cdots \circ \Phi_{A_k}^{q_k}({\Delta_{A}}(I))\right].
\end{equation*}Consequently,
 \begin{equation*}
\frac{\mathrm{curv}_*({A})}{\mathrm{curv}_{M}({A})}= \lim_{q_1\to\infty}\cdots\lim_{q_k\to\infty} \left( \frac{M_1}{\|\Phi^*_{A_1}(I)\|}\right)^{q_1}\cdots \left( \frac{M_k}{\|\Phi^*_{A_k}(I)\|}\right)^{q_k}=\infty,
\end{equation*}
\begin{equation*}
\frac{\mathrm{curv}_*({A})}{\mathrm{curv}_{M}({A})}= \lim_{q_1\to\infty}\cdots\lim_{q_k\to\infty} \left( \frac{M_1}{\|\Phi^*_{A_1}(I)\|}\right)^{q_1}\cdots \left( \frac{M_k}{\|\Phi^*_{A_k}(I)\|}\right)^{q_k}=\infty,
\end{equation*} a contradiction. Therefore, ![]() $\mathrm{curv}_{M}({A})=0.$
$\mathrm{curv}_{M}({A})=0.$
Now, we prove item (iii). If  $A\in \textbf{B}^{\mathcal U}({\mathcal H})$, then each Ai is a row contraction and, consequently,
$A\in \textbf{B}^{\mathcal U}({\mathcal H})$, then each Ai is a row contraction and, consequently,  $\|\Phi_{A_i}^*(I)\|\leq n_i$ for any
$\|\Phi_{A_i}^*(I)\|\leq n_i$ for any ![]() $i\in \{1,\ldots, k\}$. Due to item (i) when
$i\in \{1,\ldots, k\}$. Due to item (i) when ![]() $M_i:=n_i$, we have
$M_i:=n_i$, we have
Since ![]() $ \mathrm{curv} (A) \gt 0$, we also have
$ \mathrm{curv} (A) \gt 0$, we also have ![]() $\mathrm{curv}_*({A}) \gt 0$. Applying item (ii) when
$\mathrm{curv}_*({A}) \gt 0$. Applying item (ii) when ![]() $M_i:=n_i$, we conclude that
$M_i:=n_i$, we conclude that  $\|\Phi^*_{A_i}(I)\|=n_i$ for any
$\|\Phi^*_{A_i}(I)\|=n_i$ for any ![]() $i\in \{1,\ldots, k\}$, which implies
$i\in \{1,\ldots, k\}$, which implies ![]() $\mathrm{curv}_*({A})= \mathrm{curv}({A})$. This proves item (iii).
$\mathrm{curv}_*({A})= \mathrm{curv}({A})$. This proves item (iii).
If  $A\in \textbf{B}^{\mathcal U}_{reg}({\mathcal H})$, then the defect
$A\in \textbf{B}^{\mathcal U}_{reg}({\mathcal H})$, then the defect ![]() $\Delta_A(I)$ is a positive contraction. Consequently, we have
$\Delta_A(I)$ is a positive contraction. Consequently, we have ![]() $ \mathrm{trace\,}\left[{\Delta_{A}}(I)\right]\leq \mathrm{rank}\, [{\Delta_{A}}(I)]$, which proves item (iv). The proof is complete.
$ \mathrm{trace\,}\left[{\Delta_{A}}(I)\right]\leq \mathrm{rank}\, [{\Delta_{A}}(I)]$, which proves item (iv). The proof is complete.
Proposition 2.9. Let ![]() $A\in B({\mathcal H})^{n_1+\cdots + n_k}$ and
$A\in B({\mathcal H})^{n_1+\cdots + n_k}$ and ![]() $A' \in B({\mathcal H}')^{n_1+\cdots + n_k}$ be k-tuples of
$A' \in B({\mathcal H}')^{n_1+\cdots + n_k}$ be k-tuples of ![]() ${\mathcal U}$-commuting and
${\mathcal U}$-commuting and ![]() ${\mathcal U}'$-commuting operators, respectively, with positive trace class defect operators. Then,
${\mathcal U}'$-commuting operators, respectively, with positive trace class defect operators. Then, ![]() $A\oplus A' $ is a k-tuple of
$A\oplus A' $ is a k-tuple of ![]() ${\mathcal U}\oplus {\mathcal U}'$-commuting operators with a positive trace class defect operator and
${\mathcal U}\oplus {\mathcal U}'$-commuting operators with a positive trace class defect operator and
If, in addition, ![]() $\dim{\mathcal H}' \lt \infty$, then
$\dim{\mathcal H}' \lt \infty$, then ![]() $\mathrm{curv}_M({A}\oplus {A}')=\mathrm{curv}_M({A})$.
$\mathrm{curv}_M({A}\oplus {A}')=\mathrm{curv}_M({A})$.
Proof. It is straightforward due to either theorem 2.5 or corollary 2.6.
3. The curvature and the noncommutative Berezin kernel on  ${\mathcal U}$-twisted polyballs
${\mathcal U}$-twisted polyballs
Under the assumption that A is in the ![]() ${\mathcal U}$-twisted polyball
${\mathcal U}$-twisted polyball ![]() $ B^{\mathcal U}({\mathcal H})$ and has a positive trace class defect operator
$ B^{\mathcal U}({\mathcal H})$ and has a positive trace class defect operator ![]() $\Delta_A(I)$, we established several asymptotic formulas for the curvature invariant in terms of the noncommutative Berezin kernel associated with A. We also show that the curvature is upper semi-continuous.
$\Delta_A(I)$, we established several asymptotic formulas for the curvature invariant in terms of the noncommutative Berezin kernel associated with A. We also show that the curvature is upper semi-continuous.
Definition. We say that ![]() $V:=(V_1,\ldots, V_k)$ is a k-tuple of doubly
$V:=(V_1,\ldots, V_k)$ is a k-tuple of doubly ![]() ${\mathcal U}$-commuting row isometries
${\mathcal U}$-commuting row isometries ![]() $V_i:=[V_{i,1}\cdots V_{i,n_i}]$ with
$V_i:=[V_{i,1}\cdots V_{i,n_i}]$ with ![]() $V_{i,s}\in B({\mathcal H})$ if
$V_{i,s}\in B({\mathcal H})$ if
 \begin{equation*}
V_{i,s} \in {\mathcal U}' \quad \text{and } \quad V_{i,s}^* V_{j,t}=U_{i,j}(s,t)^*V_{j,t}V_{i,s}^*, \qquad (i,j,s,t)\in \Gamma.
\end{equation*}
\begin{equation*}
V_{i,s} \in {\mathcal U}' \quad \text{and } \quad V_{i,s}^* V_{j,t}=U_{i,j}(s,t)^*V_{j,t}V_{i,s}^*, \qquad (i,j,s,t)\in \Gamma.
\end{equation*} The above doubly ![]() ${\mathcal U}$-commutation relation implies the
${\mathcal U}$-commutation relation implies the ![]() ${\mathcal U}$-commutation relation
${\mathcal U}$-commutation relation ![]() $V_{i,s} V_{j,t}=U_{i,j}(s,t)V_{j,t}V_{i,s}$ for any
$V_{i,s} V_{j,t}=U_{i,j}(s,t)V_{j,t}V_{i,s}$ for any ![]() $(i,j,s,t)\in \Gamma$ (see [Reference Popescu27]). Therefore, V is also a
$(i,j,s,t)\in \Gamma$ (see [Reference Popescu27]). Therefore, V is also a ![]() ${\mathcal U}$-commuting k-tuple.
${\mathcal U}$-commuting k-tuple.
In what follows, we fix a set  ${\mathcal U}:=\left\{U_{i,j}(s,t)\right\}_{(i,j,s,t)\in \Gamma}\subset B({\mathcal H})$ of commuting unitary operators such that
${\mathcal U}:=\left\{U_{i,j}(s,t)\right\}_{(i,j,s,t)\in \Gamma}\subset B({\mathcal H})$ of commuting unitary operators such that ![]() $
U_{j,i}(t,s)=U_{i,j}(s,t)^*$ for
$
U_{j,i}(t,s)=U_{i,j}(s,t)^*$ for ![]() $ (i,j,s,t)\in \Gamma$. We recall the definition of the standard
$ (i,j,s,t)\in \Gamma$. We recall the definition of the standard ![]() $I\otimes {\mathcal U}$-twisted multi-shift
$I\otimes {\mathcal U}$-twisted multi-shift ![]() $\textbf{S}:=(\textbf{S}_1,\ldots, \textbf{S}_k)$ acting on the Hilbert space
$\textbf{S}:=(\textbf{S}_1,\ldots, \textbf{S}_k)$ acting on the Hilbert space  $\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal H}$, where
$\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal H}$, where  ${\mathbb F}_{n_i}^+$ is the unital free semigroup with generators
${\mathbb F}_{n_i}^+$ is the unital free semigroup with generators  $g^i_1,\ldots g_{n_i}^i$ and neutral element g i0. Let
$g^i_1,\ldots g_{n_i}^i$ and neutral element g i0. Let ![]() $\{\chi_{(\alpha_1,\ldots, \alpha_k)}\}$,
$\{\chi_{(\alpha_1,\ldots, \alpha_k)}\}$,  $\alpha_i\in {\mathbb F}_{n_i}^+$, be the orthonormal basis for
$\alpha_i\in {\mathbb F}_{n_i}^+$, be the orthonormal basis for  $\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)$. For each
$\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)$. For each ![]() $i\in \{1,\ldots, k\}$ and
$i\in \{1,\ldots, k\}$ and ![]() $s\in \{1,\ldots, n_i\}$, let
$s\in \{1,\ldots, n_i\}$, let ![]() $\textbf{S}_i:=[\textbf{S}_{i,1}\cdots \textbf{S}_{i,n_i}]$ be the row operator defined by setting
$\textbf{S}_i:=[\textbf{S}_{i,1}\cdots \textbf{S}_{i,n_i}]$ be the row operator defined by setting
 \begin{equation*}
\begin{split}
&\textbf{S}_{i,s}\left( \chi_{(\alpha_1,\ldots, \alpha_k)}\otimes h\right)\\
&\qquad \qquad :=\begin{cases} \chi_{(g_s^i\alpha_1,\alpha_2,\ldots, \alpha_k)}\otimes h, &\quad \text{if } i=1\\
\chi_{(\alpha_1,\ldots, \alpha_{i-1}, g_s^i \alpha_i, \alpha_{i+1},\ldots, \alpha_k)}\otimes \bf U_{i,1}(s,\alpha_1)\cdots \\ \qquad\bf U_{i,i-1}(s,\alpha_{i-1}) h,&\quad \text{if } i\in \{2,\ldots,k\}
\end{cases}
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
&\textbf{S}_{i,s}\left( \chi_{(\alpha_1,\ldots, \alpha_k)}\otimes h\right)\\
&\qquad \qquad :=\begin{cases} \chi_{(g_s^i\alpha_1,\alpha_2,\ldots, \alpha_k)}\otimes h, &\quad \text{if } i=1\\
\chi_{(\alpha_1,\ldots, \alpha_{i-1}, g_s^i \alpha_i, \alpha_{i+1},\ldots, \alpha_k)}\otimes \bf U_{i,1}(s,\alpha_1)\cdots \\ \qquad\bf U_{i,i-1}(s,\alpha_{i-1}) h,&\quad \text{if } i\in \{2,\ldots,k\}
\end{cases}
\end{split}
\end{equation*} for any ![]() $h\in {\mathcal H}$,
$h\in {\mathcal H}$,  $\alpha_1\in {\mathbb F}_{n_1}^+,\ldots, \alpha_{k}\in {\mathbb F}_{n_{k}}^+$, where
$\alpha_1\in {\mathbb F}_{n_1}^+,\ldots, \alpha_{k}\in {\mathbb F}_{n_{k}}^+$, where
 \begin{equation*}
\bf U_{i,j}(s, \beta)
:= \begin{cases}\prod_{b=1}^q U_{i,j}(s,j_b)&\quad \text{if }
\beta=g_{j_1}^j\cdots g_{j_q}^j\in {\mathbb F}_{n_j}^+ \\
I& \quad \text{if } \beta=g_0^j
\end{cases}
\end{equation*}
\begin{equation*}
\bf U_{i,j}(s, \beta)
:= \begin{cases}\prod_{b=1}^q U_{i,j}(s,j_b)&\quad \text{if }
\beta=g_{j_1}^j\cdots g_{j_q}^j\in {\mathbb F}_{n_j}^+ \\
I& \quad \text{if } \beta=g_0^j
\end{cases}
\end{equation*} for any ![]() $j\in \{1,\ldots, k\}$. Due to [Reference Popescu27],
$j\in \{1,\ldots, k\}$. Due to [Reference Popescu27], ![]() $\textbf{S}:=(\textbf{S}_1,\ldots, \textbf{S}_k)$ is a k-tuple of doubly
$\textbf{S}:=(\textbf{S}_1,\ldots, \textbf{S}_k)$ is a k-tuple of doubly ![]() $I\otimes{\mathcal U}$-commuting pure row isometries on the Hilbert space
$I\otimes{\mathcal U}$-commuting pure row isometries on the Hilbert space  $\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal H}$. If we need to emphasize the dependence of S on the set
$\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal H}$. If we need to emphasize the dependence of S on the set ![]() ${\mathcal U}$, we use the notation
${\mathcal U}$, we use the notation ![]() $\textbf{S}_{\mathcal U}$.
$\textbf{S}_{\mathcal U}$.
Let ![]() $A:=(A_1,\ldots, A_k) $ be a k-tuple such that its defect operator
$A:=(A_1,\ldots, A_k) $ be a k-tuple such that its defect operator
and each ![]() $A_i:=[A_{i,1}\cdots A_{i,n_i}]$ is row power bounded, i.e. there is a constant C > 0 such that
$A_i:=[A_{i,1}\cdots A_{i,n_i}]$ is row power bounded, i.e. there is a constant C > 0 such that  $\|\Phi_{A_i}^m(I)\|\leq C$ for any
$\|\Phi_{A_i}^m(I)\|\leq C$ for any ![]() $m\in {\mathbb N}$. Following [Reference Popescu28], the noncommutative Berezin kernel
$m\in {\mathbb N}$. Following [Reference Popescu28], the noncommutative Berezin kernel  $K_{A}:{\mathcal H}\to \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal H}$ associated with A is defined by setting
$K_{A}:{\mathcal H}\to \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal H}$ associated with A is defined by setting
 \begin{equation*}
K_{A}h :=\sum_{\beta_1\in {\mathbb F}_{n_1}^+,\ldots, \beta_k\in {\mathbb F}_{n_k}^+}
\chi_{(\beta_1,\ldots, \beta_k)}\otimes \Delta_{A}(I)^{1/2}A_{k,\beta_k}^*\cdots A_{1,\beta_1}^*h,\qquad h\in {\mathcal H},
\end{equation*}
\begin{equation*}
K_{A}h :=\sum_{\beta_1\in {\mathbb F}_{n_1}^+,\ldots, \beta_k\in {\mathbb F}_{n_k}^+}
\chi_{(\beta_1,\ldots, \beta_k)}\otimes \Delta_{A}(I)^{1/2}A_{k,\beta_k}^*\cdots A_{1,\beta_1}^*h,\qquad h\in {\mathcal H},
\end{equation*} where ![]() $A_{i,\beta_i}:= A_{i, p_1}\cdots A_{i,p_m}$ if
$A_{i,\beta_i}:= A_{i, p_1}\cdots A_{i,p_m}$ if  $\beta_i=g_{p_1}^i\cdots g_{p_m}^i\in {\mathbb F}_{n_i}^+$ and
$\beta_i=g_{p_1}^i\cdots g_{p_m}^i\in {\mathbb F}_{n_i}^+$ and  $A_{i, g_0^i}=I$. A simple extension of theorem 1.5 from [Reference Popescu28] is the following. We denote by
$A_{i, g_0^i}=I$. A simple extension of theorem 1.5 from [Reference Popescu28] is the following. We denote by ![]() $ vN({\mathcal U})$ the von Neumann algebra generated by
$ vN({\mathcal U})$ the von Neumann algebra generated by ![]() ${\mathcal U}$.
${\mathcal U}$.
Theorem 3.2 Let ![]() $A:=(A_1,\ldots, A_k)\in B({\mathcal H})^{n_1+\cdots+ n_k} $ be a
$A:=(A_1,\ldots, A_k)\in B({\mathcal H})^{n_1+\cdots+ n_k} $ be a ![]() ${\mathcal U}$-commuting k-tuple such that
${\mathcal U}$-commuting k-tuple such that ![]() $\Delta_A(I)\geq 0$ and each
$\Delta_A(I)\geq 0$ and each ![]() $A_i:=[A_{i,1}\cdots A_{i,n_i}]$ is row power bounded. If
$A_i:=[A_{i,1}\cdots A_{i,n_i}]$ is row power bounded. If ![]() $\textbf{S}:=(\textbf{S}_1,\ldots, \textbf{S}_k)$ with
$\textbf{S}:=(\textbf{S}_1,\ldots, \textbf{S}_k)$ with ![]() $\textbf{S}_i:=[\textbf{S}_{i,1}\cdots \textbf{S}_{i,n_i}]$ is the standard k-tuple of doubly
$\textbf{S}_i:=[\textbf{S}_{i,1}\cdots \textbf{S}_{i,n_i}]$ is the standard k-tuple of doubly ![]() $I\otimes{\mathcal U}$-commuting row isometries on the Hilbert space
$I\otimes{\mathcal U}$-commuting row isometries on the Hilbert space  $\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal H}$, then the following statements hold:
$\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal H}$, then the following statements hold:
(i) The noncommutative Berezin kernel KA is a bounded linear operator.
(ii)
 $K_A^*K_A=\lim_{q_k\to \infty}\ldots\lim_{q_1\to \infty} (id-\Phi_{A_k}^{q_k})\circ\cdots \circ (id-\Phi_{A_1}^{q_1})(I)$.
$K_A^*K_A=\lim_{q_k\to \infty}\ldots\lim_{q_1\to \infty} (id-\Phi_{A_k}^{q_k})\circ\cdots \circ (id-\Phi_{A_1}^{q_1})(I)$.(iii) For any
 $i\in \{1,\ldots, k\}$ and
$i\in \{1,\ldots, k\}$ and  $s\in \{1,\ldots, n_i\}$,
$s\in \{1,\ldots, n_i\}$,
 \begin{equation*}
K_A A_{i,s}^*=\textbf{S}_{i,s}^* K_A.
\end{equation*}
\begin{equation*}
K_A A_{i,s}^*=\textbf{S}_{i,s}^* K_A.
\end{equation*}(iv) For any
 $(i,j,s,t)\in \Gamma$,
$(i,j,s,t)\in \Gamma$,
 \begin{equation*}K_AU=(I\otimes U)K_A,\qquad U\in vN({\mathcal U}).\end{equation*}
\begin{equation*}K_AU=(I\otimes U)K_A,\qquad U\in vN({\mathcal U}).\end{equation*}
Proof. Note that
 \begin{equation*}
\begin{split}
\|K_Ah\|^2
&=
\left \lt \sum_{\beta_1\in {\mathbb F}_{n_1}^+,\ldots, \beta_k\in {\mathbb F}_{n_k}^+}
A_{1,\beta_1} \cdots A_{k,\beta_k} \Delta_{A}(I)A_{k,\beta_k}^*\cdots A_{1,\beta_1}^* h, h\right \gt \\
&= \left \lt \sum_{p_1,\ldots, p_k=0}^\infty \Phi_{A_1}^{p_1}\circ \cdots \circ \Phi_{A_k}^{p_k}[ \Delta_{A}(I)]h, h\right \gt \end{split}
\end{equation*}
\begin{equation*}
\begin{split}
\|K_Ah\|^2
&=
\left \lt \sum_{\beta_1\in {\mathbb F}_{n_1}^+,\ldots, \beta_k\in {\mathbb F}_{n_k}^+}
A_{1,\beta_1} \cdots A_{k,\beta_k} \Delta_{A}(I)A_{k,\beta_k}^*\cdots A_{1,\beta_1}^* h, h\right \gt \\
&= \left \lt \sum_{p_1,\ldots, p_k=0}^\infty \Phi_{A_1}^{p_1}\circ \cdots \circ \Phi_{A_k}^{p_k}[ \Delta_{A}(I)]h, h\right \gt \end{split}
\end{equation*} for any ![]() $h\in {\mathcal H}$. Due to proposition 2.3, for any
$h\in {\mathcal H}$. Due to proposition 2.3, for any ![]() $q_1,\ldots, q_k\in {\mathbb N}$,
$q_1,\ldots, q_k\in {\mathbb N}$,
 \begin{equation*}
\sum_{p_k=0}^{q_k-1} \cdots \sum_{p_1=0}^{q_1-1}\Phi_{A_k}^{p_k}\circ\cdots\circ \Phi_{A_1}^{p_1} (\Delta_A(I))
=(id-\Phi_{A_k}^{q_k})\circ\cdots \circ (id-\Phi_{A_1}^{q_1})(I).
\end{equation*}
\begin{equation*}
\sum_{p_k=0}^{q_k-1} \cdots \sum_{p_1=0}^{q_1-1}\Phi_{A_k}^{p_k}\circ\cdots\circ \Phi_{A_1}^{p_1} (\Delta_A(I))
=(id-\Phi_{A_k}^{q_k})\circ\cdots \circ (id-\Phi_{A_1}^{q_1})(I).
\end{equation*} Since the latter product is a sum of 2k terms of the form  $\pm \Phi_{A_{i_1}}^{q_{i_1}}\circ \cdots \circ \Phi_{A_{i_p}}^{q_{i_p}}(I)$ and there is C > 0 such that
$\pm \Phi_{A_{i_1}}^{q_{i_1}}\circ \cdots \circ \Phi_{A_{i_p}}^{q_{i_p}}(I)$ and there is C > 0 such that  $\|\Phi^m_{A_i}(I)\|\leq C$ for any
$\|\Phi^m_{A_i}(I)\|\leq C$ for any ![]() $m\in {\mathbb N}$ and
$m\in {\mathbb N}$ and ![]() $i\in \{1,\ldots,k\}$, we have
$i\in \{1,\ldots,k\}$, we have  $\|(id-\Phi_{A_k}^{q_k})\circ\cdots \circ (id-\Phi_{A_1}^{q_1})(I)\|\leq C^k 2^k$ for any
$\|(id-\Phi_{A_k}^{q_k})\circ\cdots \circ (id-\Phi_{A_1}^{q_1})(I)\|\leq C^k 2^k$ for any ![]() $q_1,\ldots, q_k\in {\mathbb Z}_+$. Consequently, taking into account that
$q_1,\ldots, q_k\in {\mathbb Z}_+$. Consequently, taking into account that  $\sum_{p_k=0}^{q_k-1} \cdots \sum_{p_1=0}^{q_1-1}\Phi_{A_k}^{p_k}\circ\cdots\circ \Phi_{A_1}^{p_1} (\Delta_A(I))$ is an increasing multi-sequence of positive operators with respect to the indices
$\sum_{p_k=0}^{q_k-1} \cdots \sum_{p_1=0}^{q_1-1}\Phi_{A_k}^{p_k}\circ\cdots\circ \Phi_{A_1}^{p_1} (\Delta_A(I))$ is an increasing multi-sequence of positive operators with respect to the indices ![]() $q_1,\ldots, q_k$, we conclude that KA is a bounded linear operator and item (ii) holds. The proof of items (iii) and (iv) is similar to the one corresponding to the particular case when A is in the regular
$q_1,\ldots, q_k$, we conclude that KA is a bounded linear operator and item (ii) holds. The proof of items (iii) and (iv) is similar to the one corresponding to the particular case when A is in the regular ![]() ${\mathcal U}$-twisted polyball (see theorem 1.5 from [Reference Popescu28]). We shall omit it.
${\mathcal U}$-twisted polyball (see theorem 1.5 from [Reference Popescu28]). We shall omit it.
Under the assumption that A is in the ![]() ${\mathcal U}$-twisted polyball
${\mathcal U}$-twisted polyball ![]() $ B^{\mathcal U}({\mathcal H})$ and has positive trace class defect operator
$ B^{\mathcal U}({\mathcal H})$ and has positive trace class defect operator ![]() $\Delta_A(I)$, we established several asymptotic formulas for the curvature invariant in terms of the noncommutative Berezin kernel associated with A.
$\Delta_A(I)$, we established several asymptotic formulas for the curvature invariant in terms of the noncommutative Berezin kernel associated with A.
For each  $(q_1,\ldots, q_k)\in {\mathbb Z}_+^k$, let
$(q_1,\ldots, q_k)\in {\mathbb Z}_+^k$, let ![]() $P_{(q_1,\ldots, q_k)}$ be the orthogonal projection of
$P_{(q_1,\ldots, q_k)}$ be the orthogonal projection of  $\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)$ onto the subspace
$\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)$ onto the subspace
 \begin{equation*}
\mathrm{span}\, \{\chi_{ (\alpha_1,\ldots, \alpha_k)}: \ \alpha_i\in {\mathbb F}_{n_i}^+, |\alpha_i|=q_i\}.
\end{equation*}
\begin{equation*}
\mathrm{span}\, \{\chi_{ (\alpha_1,\ldots, \alpha_k)}: \ \alpha_i\in {\mathbb F}_{n_i}^+, |\alpha_i|=q_i\}.
\end{equation*} We also denote by ![]() $P_{\leq (q_1,\ldots, q_k)}$ the orthogonal projection of
$P_{\leq (q_1,\ldots, q_k)}$ the orthogonal projection of  $\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)$ onto the subspace
$\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)$ onto the subspace
 \begin{equation*}
\mathrm{span}\, \{\chi_{ (\alpha_1,\ldots, \alpha_k)}: \ \alpha_i\in {\mathbb F}_{n_i}^+, |\alpha_i|\leq q_i\}.
\end{equation*}
\begin{equation*}
\mathrm{span}\, \{\chi_{ (\alpha_1,\ldots, \alpha_k)}: \ \alpha_i\in {\mathbb F}_{n_i}^+, |\alpha_i|\leq q_i\}.
\end{equation*}Theorem 3.3 Let A be in the ![]() ${\mathcal U}$-twisted polyball
${\mathcal U}$-twisted polyball  $ \textbf{B}^{\mathcal U}({\mathcal H})$ such that
$ \textbf{B}^{\mathcal U}({\mathcal H})$ such that ![]() $\Delta_A(I)$ is a positive trace class operator. Then, the M-curvature of A satisfies the asymptotic formulas
$\Delta_A(I)$ is a positive trace class operator. Then, the M-curvature of A satisfies the asymptotic formulas
 \begin{equation*}\begin{split}
\mathrm{curv}_M({A})&=
\lim_{m\to\infty}\frac{1}{\left(\begin{matrix} m+k\\ k\end{matrix}\right)}\sum_{{q_1\geq 0,\ldots, q_k\geq 0}\atop {q_1+\cdots +q_k\leq m}} \frac{
\mathrm{trace\,}\left[ {K_{A}^*} (P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal H}){K_{A}}\right]}{M_1^{q_1}\cdots M_k^{q_k}} \\
&=
\lim_{(q_1,\ldots, q_k)\in {\mathbb Z}_+^k} \frac{
\mathrm{trace\,}\left[ {K_{A}^*} (P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal H}){K_{A}}\right]}{M_1^{q_1}\cdots M_k^{q_k}} \\
&=\lim_{m\to\infty}\frac{1}{\left(\begin{matrix} m+k-1\\ k-1\end{matrix}\right)}\sum_{{q_1\geq 0,\ldots, q_k\geq 0}\atop {q_1+\cdots +q_k= m}}\frac{
\mathrm{trace\,}\left[ {K_{A}^*} (P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal H}){K_{A}}\right]}{M_1^{q_1}\cdots M_k^{q_k}}.
\end{split}
\end{equation*}
\begin{equation*}\begin{split}
\mathrm{curv}_M({A})&=
\lim_{m\to\infty}\frac{1}{\left(\begin{matrix} m+k\\ k\end{matrix}\right)}\sum_{{q_1\geq 0,\ldots, q_k\geq 0}\atop {q_1+\cdots +q_k\leq m}} \frac{
\mathrm{trace\,}\left[ {K_{A}^*} (P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal H}){K_{A}}\right]}{M_1^{q_1}\cdots M_k^{q_k}} \\
&=
\lim_{(q_1,\ldots, q_k)\in {\mathbb Z}_+^k} \frac{
\mathrm{trace\,}\left[ {K_{A}^*} (P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal H}){K_{A}}\right]}{M_1^{q_1}\cdots M_k^{q_k}} \\
&=\lim_{m\to\infty}\frac{1}{\left(\begin{matrix} m+k-1\\ k-1\end{matrix}\right)}\sum_{{q_1\geq 0,\ldots, q_k\geq 0}\atop {q_1+\cdots +q_k= m}}\frac{
\mathrm{trace\,}\left[ {K_{A}^*} (P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal H}){K_{A}}\right]}{M_1^{q_1}\cdots M_k^{q_k}}.
\end{split}
\end{equation*} If, in addition, ![]() $ M_i\geq 1$ for any
$ M_i\geq 1$ for any ![]() $i\in \{1,\ldots, k\}$, then
$i\in \{1,\ldots, k\}$, then
 \begin{equation*}
\mathrm{curv}_M({A})=\lim_{q_1\to\infty}\cdots\lim_{q_k\to\infty}\frac{
\mathrm{trace\,}\left[ {K_{A}^*} (P_{\leq (q_1,\ldots, q_k)}\otimes I_{\mathcal H}){K_{A}}\right]}{\prod_{i=1}^k(1+M_i +\cdots+ M_i^{q_i})}.
\end{equation*}
\begin{equation*}
\mathrm{curv}_M({A})=\lim_{q_1\to\infty}\cdots\lim_{q_k\to\infty}\frac{
\mathrm{trace\,}\left[ {K_{A}^*} (P_{\leq (q_1,\ldots, q_k)}\otimes I_{\mathcal H}){K_{A}}\right]}{\prod_{i=1}^k(1+M_i +\cdots+ M_i^{q_i})}.
\end{equation*}Proof. Let ![]() $\textbf{S}:=(\textbf{S}_1,\ldots, \textbf{S}_k)$, with
$\textbf{S}:=(\textbf{S}_1,\ldots, \textbf{S}_k)$, with ![]() $\textbf{S}_i:=(\textbf{S}_{i,1},\ldots,\textbf{S}_{i,n_i})$ being the standard k-tuple of doubly
$\textbf{S}_i:=(\textbf{S}_{i,1},\ldots,\textbf{S}_{i,n_i})$ being the standard k-tuple of doubly ![]() $I\otimes{\mathcal U}$-commuting row isometries on the Hilbert space
$I\otimes{\mathcal U}$-commuting row isometries on the Hilbert space  $\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal H}$. Note that
$\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal H}$. Note that
 \begin{equation*}
\begin{split}
&\textbf{S}_{i,s}^*\left( \chi_{(\alpha_1,\ldots, \alpha_k)}\otimes h\right)\\
&\qquad \qquad =\begin{cases}
\chi_{(\alpha_1,\ldots, \alpha_{i-1}, \beta_i, \alpha_{i+1},\ldots, \alpha_k)}\otimes \bf{U}_{i,1}(s,\alpha_1)^*\cdots \\ \qquad \bf{U}_{i,i-1}(s,\alpha_{i-1})^*h,&\quad \text{if } \alpha_i=g_s^i \beta_i\\
0, &\quad \text{otherwise }
\end{cases}
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
&\textbf{S}_{i,s}^*\left( \chi_{(\alpha_1,\ldots, \alpha_k)}\otimes h\right)\\
&\qquad \qquad =\begin{cases}
\chi_{(\alpha_1,\ldots, \alpha_{i-1}, \beta_i, \alpha_{i+1},\ldots, \alpha_k)}\otimes \bf{U}_{i,1}(s,\alpha_1)^*\cdots \\ \qquad \bf{U}_{i,i-1}(s,\alpha_{i-1})^*h,&\quad \text{if } \alpha_i=g_s^i \beta_i\\
0, &\quad \text{otherwise }
\end{cases}
\end{split}
\end{equation*} for any ![]() $h\in {\mathcal H}$,
$h\in {\mathcal H}$,  $\alpha_1\in {\mathbb F}_{n_1}^+,\ldots, \alpha_{k}\in {\mathbb F}_{n_{k}}^+$, and
$\alpha_1\in {\mathbb F}_{n_1}^+,\ldots, \alpha_{k}\in {\mathbb F}_{n_{k}}^+$, and  $\beta_i\in {\mathbb F}_{n_i}^+$, and, consequently,
$\beta_i\in {\mathbb F}_{n_i}^+$, and, consequently,
 \begin{equation*}
\begin{split}
&\sum_{s=1}^{n_i} \textbf{S}_{i,s}\textbf{S}_{i,s}^*\left( \chi_{(\alpha_1,\ldots, \alpha_k)}\otimes h\right)
\\
& =\begin{cases}
\chi_{(\alpha_1,\ldots, \alpha_{i-1}, \alpha_i, \alpha_{i+1},\ldots, \alpha_k)}\otimes \bf{U}_{i,1}(s,\alpha_1)\bf{U}_{i,1}(s,\alpha_1)^* \cdots \\ \qquad \bf{U}_{i,i-1}(s,\alpha_{i-1})\bf{U}_{i,i-1}(s,\alpha_{i-1})^*h,&\quad \text{if } |\alpha_i|\geq 1\\
0, &\quad \text{otherwise }
\end{cases}\\
& =\begin{cases}
\chi_{(\alpha_1,\ldots, \alpha_k)}\otimes h,&\quad \text{if } |\alpha_i|\geq 1\\
0, &\quad \text{otherwise.}
\end{cases}
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
&\sum_{s=1}^{n_i} \textbf{S}_{i,s}\textbf{S}_{i,s}^*\left( \chi_{(\alpha_1,\ldots, \alpha_k)}\otimes h\right)
\\
& =\begin{cases}
\chi_{(\alpha_1,\ldots, \alpha_{i-1}, \alpha_i, \alpha_{i+1},\ldots, \alpha_k)}\otimes \bf{U}_{i,1}(s,\alpha_1)\bf{U}_{i,1}(s,\alpha_1)^* \cdots \\ \qquad \bf{U}_{i,i-1}(s,\alpha_{i-1})\bf{U}_{i,i-1}(s,\alpha_{i-1})^*h,&\quad \text{if } |\alpha_i|\geq 1\\
0, &\quad \text{otherwise }
\end{cases}\\
& =\begin{cases}
\chi_{(\alpha_1,\ldots, \alpha_k)}\otimes h,&\quad \text{if } |\alpha_i|\geq 1\\
0, &\quad \text{otherwise.}
\end{cases}
\end{split}
\end{equation*} Since ![]() $\textbf{S}:=(\textbf{S}_1,\ldots, \textbf{S}_k) $ with
$\textbf{S}:=(\textbf{S}_1,\ldots, \textbf{S}_k) $ with ![]() $\textbf{S}_i:=(\textbf{S}_{i,1},\ldots,\textbf{S}_{i,n_i})$ is k-tuple of doubly
$\textbf{S}_i:=(\textbf{S}_{i,1},\ldots,\textbf{S}_{i,n_i})$ is k-tuple of doubly ![]() $I\otimes{\mathcal U}$-commuting row isometries and
$I\otimes{\mathcal U}$-commuting row isometries and  ${\mathcal U}:=\left\{U_{i,j}(s,t)\right\}_{(i,j,s,t)\in \Gamma}$ is a set of commuting unitary operators on a Hilbert space
${\mathcal U}:=\left\{U_{i,j}(s,t)\right\}_{(i,j,s,t)\in \Gamma}$ is a set of commuting unitary operators on a Hilbert space ![]() ${\mathcal H}$ such that
${\mathcal H}$ such that ![]() $
U_{j,i}(t,s)=U_{i,j}(s,t)^*$ for
$
U_{j,i}(t,s)=U_{i,j}(s,t)^*$ for ![]() $(i,j,s,t)\in \Gamma,
$ one can use the
$(i,j,s,t)\in \Gamma,
$ one can use the ![]() $I\otimes {\mathcal U}$-commutation relations for S to check that
$I\otimes {\mathcal U}$-commutation relations for S to check that
for any ![]() $i,j\in \{1,\ldots, k\}$, i ≠ j,
$i,j\in \{1,\ldots, k\}$, i ≠ j, ![]() $s\in \{1,\ldots, n_i\}$,
$s\in \{1,\ldots, n_i\}$, ![]() $t\in \{1,\ldots, n_j\}$. Moreover, for any
$t\in \{1,\ldots, n_j\}$. Moreover, for any ![]() $i_1,\ldots, i_p$ distinct elements in
$i_1,\ldots, i_p$ distinct elements in ![]() $\{1,\ldots, k\}$ and
$\{1,\ldots, k\}$ and  $\alpha_1\in {\mathbb F}_{n_{i_1}}^+$,…,
$\alpha_1\in {\mathbb F}_{n_{i_1}}^+$,…,  $\alpha_p\in {\mathbb F}_{n_{i_p}}^+$, one can prove that
$\alpha_p\in {\mathbb F}_{n_{i_p}}^+$, one can prove that
 \begin{equation}
\left(\textbf{S}_{i_1,\alpha_1}\textbf{S}_{i_1,\alpha_1}^*\right)\cdots \left(\textbf{S}_{i_p,\alpha_p}\textbf{S}_{i_p,\alpha_p}^*\right)
=\textbf{S}_{i_1,\alpha_1}\cdots \textbf{S}_{i_p,\alpha_p} \textbf{S}_{i_p,\alpha_p}^*\cdots \textbf{S}_{i_1,\alpha_1}^*.
\end{equation}
\begin{equation}
\left(\textbf{S}_{i_1,\alpha_1}\textbf{S}_{i_1,\alpha_1}^*\right)\cdots \left(\textbf{S}_{i_p,\alpha_p}\textbf{S}_{i_p,\alpha_p}^*\right)
=\textbf{S}_{i_1,\alpha_1}\cdots \textbf{S}_{i_p,\alpha_p} \textbf{S}_{i_p,\alpha_p}^*\cdots \textbf{S}_{i_1,\alpha_1}^*.
\end{equation}Consequently, it is easy to see that
 \begin{equation*}(id-\Phi_{\textbf{S}_1})\circ \cdots \circ (id-\Phi_{\textbf{S}_k})(I)=\prod_{i=1}^k\left(I-\sum_{s=1}^{n_i} \textbf{S}_{i,s}\textbf{S}_{i,s}^*\right)=
{P}_{\mathbb C}\otimes I_{\mathcal H},
\end{equation*}
\begin{equation*}(id-\Phi_{\textbf{S}_1})\circ \cdots \circ (id-\Phi_{\textbf{S}_k})(I)=\prod_{i=1}^k\left(I-\sum_{s=1}^{n_i} \textbf{S}_{i,s}\textbf{S}_{i,s}^*\right)=
{P}_{\mathbb C}\otimes I_{\mathcal H},
\end{equation*} where ![]() ${P}_{\mathbb C}$ is the orthogonal projection of
${P}_{\mathbb C}$ is the orthogonal projection of  $\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)$ onto
$\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)$ onto  ${\mathbb C} \subset \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)$, where
${\mathbb C} \subset \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)$, where ![]() ${\mathbb C} $ is identified with
${\mathbb C} $ is identified with  $\chi_{(g_0^1,\ldots, g_0^k)} {\mathbb C}$. On the other hand, one can check that
$\chi_{(g_0^1,\ldots, g_0^k)} {\mathbb C}$. On the other hand, one can check that
 \begin{equation*}
\begin{split}
\left(\sum_{\alpha\in {\mathbb F}_{n_i}^+, |\alpha|=q_i} \textbf{S}_{i,\alpha} \textbf{S}_{i,\alpha}^*\right)\left( \chi_{(\alpha_1,\ldots, \alpha_k)}\otimes h\right)
=\begin{cases}
\chi_{(\alpha_1,\ldots, \alpha_k)}\otimes h,&\quad \text{if } |\alpha_i|\geq q_i\\
0, &\quad \text{otherwise }
\end{cases}
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
\left(\sum_{\alpha\in {\mathbb F}_{n_i}^+, |\alpha|=q_i} \textbf{S}_{i,\alpha} \textbf{S}_{i,\alpha}^*\right)\left( \chi_{(\alpha_1,\ldots, \alpha_k)}\otimes h\right)
=\begin{cases}
\chi_{(\alpha_1,\ldots, \alpha_k)}\otimes h,&\quad \text{if } |\alpha_i|\geq q_i\\
0, &\quad \text{otherwise }
\end{cases}
\end{split}
\end{equation*} for any ![]() $q_i\in {\mathbb N}$. Hence, we deduce that
$q_i\in {\mathbb N}$. Hence, we deduce that
 \begin{equation*}
\begin{split}
&(\Phi_{\textbf{S}_i}^{q_i}-\Phi_{\textbf{S}_i}^{q_i+1})(I)\left( \chi_{(\alpha_1,\ldots, \alpha_k)}\otimes h\right)
\\
&\qquad\qquad=
\left(\sum_{\alpha\in {\mathbb F}_{n_i}^+, |\alpha|=q_i} \textbf{S}_{i,\alpha} \textbf{S}_{i,\alpha}^*
-\sum_{\alpha\in {\mathbb F}_{n_i}^+, |\alpha|=q_i+1} \textbf{S}_{i,\alpha} \textbf{S}_{i,\alpha}^*
\right)\left( \chi_{(\alpha_1,\ldots, \alpha_k)}\otimes h\right)\\
&\qquad\qquad =\begin{cases}
\chi_{(\alpha_1,\ldots, \alpha_k)}\otimes h,&\quad \text{if } |\alpha_i|= q_i\\
0, &\quad \text{otherwise. }
\end{cases}
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
&(\Phi_{\textbf{S}_i}^{q_i}-\Phi_{\textbf{S}_i}^{q_i+1})(I)\left( \chi_{(\alpha_1,\ldots, \alpha_k)}\otimes h\right)
\\
&\qquad\qquad=
\left(\sum_{\alpha\in {\mathbb F}_{n_i}^+, |\alpha|=q_i} \textbf{S}_{i,\alpha} \textbf{S}_{i,\alpha}^*
-\sum_{\alpha\in {\mathbb F}_{n_i}^+, |\alpha|=q_i+1} \textbf{S}_{i,\alpha} \textbf{S}_{i,\alpha}^*
\right)\left( \chi_{(\alpha_1,\ldots, \alpha_k)}\otimes h\right)\\
&\qquad\qquad =\begin{cases}
\chi_{(\alpha_1,\ldots, \alpha_k)}\otimes h,&\quad \text{if } |\alpha_i|= q_i\\
0, &\quad \text{otherwise. }
\end{cases}
\end{split}
\end{equation*}Consequently, using relation (3.1), we obtain
 \begin{equation}
\begin{split}
&(\Phi_{\textbf{S}_1}^{q_1}- \Phi_{\textbf{S}_1}^{q_1+1})\circ \cdots \circ (\Phi_{\textbf{S}_k}^{q_k}- \Phi_{\textbf{S}_k}^{q_k+1})(I) \\ \qquad
& \qquad =\prod_{i=1}^k \left(\sum_{\alpha\in {\mathbb F}_{n_i}^+, |\alpha|=q} \textbf{S}_{i,\alpha} \textbf{S}_{i,\alpha}^*
-\sum_{\alpha\in {\mathbb F}_{n_i}^+, |\alpha|=q_i+1} \textbf{S}_{i,\alpha} \textbf{S}_{i,\alpha}^*
\right)\\
& \qquad =P_{(q_1,\ldots, q_k)} \otimes I_{\mathcal H}.
\end{split}
\end{equation}
\begin{equation}
\begin{split}
&(\Phi_{\textbf{S}_1}^{q_1}- \Phi_{\textbf{S}_1}^{q_1+1})\circ \cdots \circ (\Phi_{\textbf{S}_k}^{q_k}- \Phi_{\textbf{S}_k}^{q_k+1})(I) \\ \qquad
& \qquad =\prod_{i=1}^k \left(\sum_{\alpha\in {\mathbb F}_{n_i}^+, |\alpha|=q} \textbf{S}_{i,\alpha} \textbf{S}_{i,\alpha}^*
-\sum_{\alpha\in {\mathbb F}_{n_i}^+, |\alpha|=q_i+1} \textbf{S}_{i,\alpha} \textbf{S}_{i,\alpha}^*
\right)\\
& \qquad =P_{(q_1,\ldots, q_k)} \otimes I_{\mathcal H}.
\end{split}
\end{equation}On the other hand, due to theorem 3.2, we have
 \begin{equation*}
K_A^*K_A=\lim_{q_k\to \infty}\ldots\lim_{q_1\to \infty} (id-\Phi_{A_k}^{q_k})\circ\cdots \circ (id-\Phi_{A_1}^{q_1})(I),
\end{equation*}
\begin{equation*}
K_A^*K_A=\lim_{q_k\to \infty}\ldots\lim_{q_1\to \infty} (id-\Phi_{A_k}^{q_k})\circ\cdots \circ (id-\Phi_{A_1}^{q_1})(I),
\end{equation*}where the limits are in the weak operator topology. Since
 \begin{equation*}
0\leq (id-\Phi_{A_k}^{q_k})\circ \cdots \circ (id-\Phi_{A_1}^{q_1})(I)
=\sum_{s_k=0}^{q_k-1}\Phi_{A_k}^{s_k}\circ\cdots \sum_{s_1=0}^{q_1-1}\Phi_{A_1}^{s_1}\circ
(id-\Phi_{A_k})\circ \cdots \circ (id-\Phi_{A_1})(I)
\end{equation*}
\begin{equation*}
0\leq (id-\Phi_{A_k}^{q_k})\circ \cdots \circ (id-\Phi_{A_1}^{q_1})(I)
=\sum_{s_k=0}^{q_k-1}\Phi_{A_k}^{s_k}\circ\cdots \sum_{s_1=0}^{q_1-1}\Phi_{A_1}^{s_1}\circ
(id-\Phi_{A_k})\circ \cdots \circ (id-\Phi_{A_1})(I)
\end{equation*} and ![]() $\Delta_A(I):=(id-\Phi_{A_k})\circ \cdots \circ (id-\Phi_{A_1})(I)\geq 0$, the sequence
$\Delta_A(I):=(id-\Phi_{A_k})\circ \cdots \circ (id-\Phi_{A_1})(I)\geq 0$, the sequence  $\{(id-\Phi_{T_k}^{q_k})\circ \cdots \circ (id-\Phi_{T_1}^{q_1})(I)\}_{(q_1,\ldots, q_k)\in {\mathbb Z}_+^k}$ is increasing with respect to each index qi. Using proposition 2.3, the fact that
$\{(id-\Phi_{T_k}^{q_k})\circ \cdots \circ (id-\Phi_{T_1}^{q_1})(I)\}_{(q_1,\ldots, q_k)\in {\mathbb Z}_+^k}$ is increasing with respect to each index qi. Using proposition 2.3, the fact that ![]() $\Phi_{A_1},\ldots, \Phi_{A_k}$ are WOT-continuous completely positive and contractive linear maps, and WOT-
$\Phi_{A_1},\ldots, \Phi_{A_k}$ are WOT-continuous completely positive and contractive linear maps, and WOT- $\lim_{q_i\to \infty} \Phi_{A_i}^{q_i}(I)$ exists for each
$\lim_{q_i\to \infty} \Phi_{A_i}^{q_i}(I)$ exists for each ![]() $i\in \{1,\ldots, k\}$, we deduce that
$i\in \{1,\ldots, k\}$, we deduce that
 \begin{equation*}
\begin{split}
(id-\Phi_{A_1})({K_{A}^*}{K_{A}})
&=\lim_{q_k\to\infty}\ldots \lim_{q_1\to\infty} (id-\Phi_{A_k}^{q_k})\circ \cdots \circ (id-\Phi_{A_1}^{q_1})\circ(id-\Phi_{A_1})(I)\\
&=\lim_{q_k\to\infty}\ldots \lim_{q_2\to\infty} (id-\Phi_{A_k}^{q_k})\circ \cdots \circ (id-\Phi_{A_2}^{q_2}) \\ \quad
&\qquad\left[\lim_{q_1\to\infty}(id-\Phi_{A_1}^{q_1})\circ(id-\Phi_{A_1})(I)\right]\\
&=\lim_{q_k\to\infty}\ldots \lim_{q_2\to\infty} (id-\Phi_{A_k}^{q_k})\circ \cdots \circ (id-\Phi_{A_2}^{q_2})\circ(id-\Phi_{A_1})(I).
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
(id-\Phi_{A_1})({K_{A}^*}{K_{A}})
&=\lim_{q_k\to\infty}\ldots \lim_{q_1\to\infty} (id-\Phi_{A_k}^{q_k})\circ \cdots \circ (id-\Phi_{A_1}^{q_1})\circ(id-\Phi_{A_1})(I)\\
&=\lim_{q_k\to\infty}\ldots \lim_{q_2\to\infty} (id-\Phi_{A_k}^{q_k})\circ \cdots \circ (id-\Phi_{A_2}^{q_2}) \\ \quad
&\qquad\left[\lim_{q_1\to\infty}(id-\Phi_{A_1}^{q_1})\circ(id-\Phi_{A_1})(I)\right]\\
&=\lim_{q_k\to\infty}\ldots \lim_{q_2\to\infty} (id-\Phi_{A_k}^{q_k})\circ \cdots \circ (id-\Phi_{A_2}^{q_2})\circ(id-\Phi_{A_1})(I).
\end{split}
\end{equation*} Consequently, composing to the left by ![]() $id-\Phi_{A_2}$, a similar reasoning leads to
$id-\Phi_{A_2}$, a similar reasoning leads to
 \begin{align*}
(id-\Phi_{A_2})\circ(id-\Phi_{A_1})({K_{A}^*}{K_{A}})=&\lim_{q_k\to\infty}\ldots \lim_{q_3\to\infty} (id-\Phi_{A_k}^{q_k})\circ \cdots \circ (id-\Phi_{A_3}^{q_3})\circ\\ &(id-\Phi_{A_1})\circ(id-\Phi_{A_2})(I).
\end{align*}
\begin{align*}
(id-\Phi_{A_2})\circ(id-\Phi_{A_1})({K_{A}^*}{K_{A}})=&\lim_{q_k\to\infty}\ldots \lim_{q_3\to\infty} (id-\Phi_{A_k}^{q_k})\circ \cdots \circ (id-\Phi_{A_3}^{q_3})\circ\\ &(id-\Phi_{A_1})\circ(id-\Phi_{A_2})(I).
\end{align*}Continuing this process, we obtain
On the other hand, due to theorem 3.2, we have ![]() ${K_{A}} {A}^*_{i,j}= \textbf{S}_{i,j}^* {K_{A}}
$ for any
${K_{A}} {A}^*_{i,j}= \textbf{S}_{i,j}^* {K_{A}}
$ for any ![]() $i\in \{1,\ldots, k\}$ and any
$i\in \{1,\ldots, k\}$ and any ![]() $j\in \{1,\ldots, n_i\}$. Consequently, we deduce that
$j\in \{1,\ldots, n_i\}$. Consequently, we deduce that
 \begin{equation*} \begin{split}
{K_{A}^*}&\left[ \Phi_{\textbf{S}_1}^{q_1}\circ \cdots \circ \Phi_{\textbf{S}_k}^{q_k}\circ(id-\Phi_{\textbf{S}_k})\circ \cdots \circ (id-\Phi_{\textbf{S}_1})(I) \right]{K_{A}}\\
&\qquad \qquad=\Phi_{A_1}^{q_1}\circ \cdots \circ \Phi_{A_k}^{q_k}\circ(id-\Phi_{A_1})\circ \cdots \circ (id-\Phi_{A_k})({K_{A}^*}{K_{A}}).
\end{split}
\end{equation*}
\begin{equation*} \begin{split}
{K_{A}^*}&\left[ \Phi_{\textbf{S}_1}^{q_1}\circ \cdots \circ \Phi_{\textbf{S}_k}^{q_k}\circ(id-\Phi_{\textbf{S}_k})\circ \cdots \circ (id-\Phi_{\textbf{S}_1})(I) \right]{K_{A}}\\
&\qquad \qquad=\Phi_{A_1}^{q_1}\circ \cdots \circ \Phi_{A_k}^{q_k}\circ(id-\Phi_{A_1})\circ \cdots \circ (id-\Phi_{A_k})({K_{A}^*}{K_{A}}).
\end{split}
\end{equation*}Hence and using relations (3.2) and (3.3), we deduce that
 \begin{equation*}
\begin{split}
{K_{A}^*} (P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal H}){K_{A}}
&={K_{A}^*}\left[ (\Phi_{\textbf{S}_1}^{q_1}- \Phi_{\textbf{S}_1}^{q_1+1})\circ \cdots \circ (\Phi_{\textbf{S}_k}^{q_k}- \Phi_{\textbf{S}_k}^{q_k+1})(I) \right]{K_{A}}\\
&={K_{A}^*}\left[ \Phi_{\textbf{S}_1}^{q_1} \circ \cdots \circ \Phi_{\textbf{S}_k}^{q_k}\circ(id-\Phi_{\textbf{S}_k})\circ \cdots \circ (id-\Phi_{\textbf{S}_1})(I) \right]{K_{A}}\\
&=\Phi_{A_1}^{q_1}\circ \cdots \circ \Phi_{A_k}^{q_k}\circ(id-\Phi_{A_1})\circ \cdots \circ (id-\Phi_{A_k})({K_{A}^*}{K_{A}})\\
&=\Phi_{A_1}^{q_1}\circ \cdots \circ \Phi_{A_k}^{q_k} ({\Delta_{A}}(I)).
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
{K_{A}^*} (P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal H}){K_{A}}
&={K_{A}^*}\left[ (\Phi_{\textbf{S}_1}^{q_1}- \Phi_{\textbf{S}_1}^{q_1+1})\circ \cdots \circ (\Phi_{\textbf{S}_k}^{q_k}- \Phi_{\textbf{S}_k}^{q_k+1})(I) \right]{K_{A}}\\
&={K_{A}^*}\left[ \Phi_{\textbf{S}_1}^{q_1} \circ \cdots \circ \Phi_{\textbf{S}_k}^{q_k}\circ(id-\Phi_{\textbf{S}_k})\circ \cdots \circ (id-\Phi_{\textbf{S}_1})(I) \right]{K_{A}}\\
&=\Phi_{A_1}^{q_1}\circ \cdots \circ \Phi_{A_k}^{q_k}\circ(id-\Phi_{A_1})\circ \cdots \circ (id-\Phi_{A_k})({K_{A}^*}{K_{A}})\\
&=\Phi_{A_1}^{q_1}\circ \cdots \circ \Phi_{A_k}^{q_k} ({\Delta_{A}}(I)).
\end{split}
\end{equation*}Therefore,
 \begin{equation}
{K_{A}^*} (P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal H}){K_{A}}=
\Phi_{A_1}^{q_1}\circ \cdots \circ \Phi_{A_k}^{q_k}({\Delta_{A}}(I))
\end{equation}
\begin{equation}
{K_{A}^*} (P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal H}){K_{A}}=
\Phi_{A_1}^{q_1}\circ \cdots \circ \Phi_{A_k}^{q_k}({\Delta_{A}}(I))
\end{equation} for any ![]() $q_1,\ldots,q_k\in {\mathbb Z}_+$. Using this relation, theorem 2.5, and corollary 2.6, we deduce the first three equalities in the theorem.
$q_1,\ldots,q_k\in {\mathbb Z}_+$. Using this relation, theorem 2.5, and corollary 2.6, we deduce the first three equalities in the theorem.
Assume now that ![]() $M_i\geq 1$ for any
$M_i\geq 1$ for any ![]() $i\in \{1,\ldots, k\}$. Using again theorem 2.5 and corollary 2.6, we have
$i\in \{1,\ldots, k\}$. Using again theorem 2.5 and corollary 2.6, we have
 \begin{equation*}\mathrm{curv}_M({A})=\lim_{q_1\to\infty}\cdots\lim_{q_k\to\infty} \frac{1}{M_1^{q_1}\cdots M_k^{q_k}}\mathrm{trace\,}\left[ \Phi_{A_1}^{q_1}\circ \cdots \circ \Phi_{A_k}^{q_k}({\Delta_{A}}(I))\right].
\end{equation*}
\begin{equation*}\mathrm{curv}_M({A})=\lim_{q_1\to\infty}\cdots\lim_{q_k\to\infty} \frac{1}{M_1^{q_1}\cdots M_k^{q_k}}\mathrm{trace\,}\left[ \Phi_{A_1}^{q_1}\circ \cdots \circ \Phi_{A_k}^{q_k}({\Delta_{A}}(I))\right].
\end{equation*}A repeated application of Stolz–Cesáro convergence theorem with respect to each limit leads to
 \begin{equation*}
\begin{split}
\mathrm{curv}_M({A})&=
\lim_{q_1\to\infty}\cdots\lim_{q_k\to\infty}
\frac{\mathrm{trace\,}\left[ \sum_{s_1=0}^{q_1}\cdots \sum_{s_k=0}^{q_k} \Phi_{A_1}^{s_1}\circ \cdots \circ \Phi_{A_k}^{s_k}({\Delta_{A}}(I))\right]}
{\prod_{i=1}^k(1+M_i+\cdots + M_i^{q_i})}.
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
\mathrm{curv}_M({A})&=
\lim_{q_1\to\infty}\cdots\lim_{q_k\to\infty}
\frac{\mathrm{trace\,}\left[ \sum_{s_1=0}^{q_1}\cdots \sum_{s_k=0}^{q_k} \Phi_{A_1}^{s_1}\circ \cdots \circ \Phi_{A_k}^{s_k}({\Delta_{A}}(I))\right]}
{\prod_{i=1}^k(1+M_i+\cdots + M_i^{q_i})}.
\end{split}
\end{equation*}Consequently, due to relation (3.4), we deduce that
 \begin{equation*}
\mathrm{curv}_M({A})=\lim_{q_1\to\infty}\cdots\lim_{q_k\to\infty}\frac{
\mathrm{trace\,}\left[ {K_{A}^*} (P_{\leq (q_1,\ldots, q_k)}\otimes I_{\mathcal H}){K_{A}}\right]}{\prod_{i=1}^k(1+M_i +\cdots+ M_i^{q_i})}.
\end{equation*}
\begin{equation*}
\mathrm{curv}_M({A})=\lim_{q_1\to\infty}\cdots\lim_{q_k\to\infty}\frac{
\mathrm{trace\,}\left[ {K_{A}^*} (P_{\leq (q_1,\ldots, q_k)}\otimes I_{\mathcal H}){K_{A}}\right]}{\prod_{i=1}^k(1+M_i +\cdots+ M_i^{q_i})}.
\end{equation*}The proof is complete.
In the particular case when ![]() $M=(M_1,\ldots, M_k)=(n_1,\ldots, n_k)$, we obtain the following asymptotic formulas for the curvature which will be used later on.
$M=(M_1,\ldots, M_k)=(n_1,\ldots, n_k)$, we obtain the following asymptotic formulas for the curvature which will be used later on.
Corollary 3.4. Let ![]() $A:=(A_1,\ldots, A_k)$ be an element in the
$A:=(A_1,\ldots, A_k)$ be an element in the ![]() ${\mathcal U}$-twisted polyball
${\mathcal U}$-twisted polyball  $ \textbf{B}^{\mathcal U}({\mathcal H})$ such that
$ \textbf{B}^{\mathcal U}({\mathcal H})$ such that ![]() $\Delta_A(I)$ is a positive trace class operator. Then, the curvature of A satisfies the asymptotic formulas
$\Delta_A(I)$ is a positive trace class operator. Then, the curvature of A satisfies the asymptotic formulas
 \begin{equation*}\begin{split}
\mathrm{curv}({A})&=
\lim_{m\to\infty}\frac{1}{\left(\begin{matrix} m+k\\ k\end{matrix}\right)}\sum_{{q_1\geq 0,\ldots, q_k\geq 0}\atop {q_1+\cdots +q_k\leq m}} \frac{
\mathrm{trace\,}\left[ {K_{A}^*} (P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal H}){K_{A}}\right]}
{\mathrm{trace\,}\left[P_{(q_1,\ldots, q_k)}\right]} \\
&=
\lim_{(q_1,\ldots, q_k)\in {\mathbb Z}_+^k} \frac{
\mathrm{trace\,}\left[ {K_{A}^*} (P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal H}){K_{A}}\right]}{\mathrm{trace\,}[P_{(q_1,\ldots, q_k)}]} \\
&=\lim_{m\to\infty}\frac{1}{\left(\begin{matrix} m+k-1\\ k-1\end{matrix}\right)}\sum_{{q_1\geq 0,\ldots, q_k\geq 0}\atop {q_1+\cdots +q_k= m}}\frac{
\mathrm{trace\,}\left[ {K_{A}^*} (P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal H}){K_{A}}\right]}{\mathrm{trace\,}[P_{(q_1,\ldots, q_k)}]}\\
&=\lim_{q_1\to\infty}\cdots\lim_{q_k\to\infty}\frac{
\mathrm{trace\,}\left[ {K_{A}^*} (P_{\leq (q_1,\ldots, q_k)}\otimes I_{\mathcal H}){K_{A}}\right]}{\mathrm{trace\,}[P_{\leq (q_1,\ldots, q_k)}]}\\
&=\lim_{m\to\infty}\frac{1}{\left(\begin{matrix} m+k\\ k\end{matrix}\right)}\sum_{{q_1\geq 0,\ldots, q_k\geq 0}\atop {q_1+\cdots +q_k\leq m}}\frac {1}{n_1^{q_1}\cdots n_k^{q_k}}{\mathrm{trace\,}\left[ \Phi_{A_1}^{q_1}\circ \cdots \circ \Phi_{A_k}^{q_k}({\Delta_{A}}(I))\right]}\\
&=\lim_{m\to\infty}\frac{1}{\left(\begin{matrix} m+k-1\\ k-1\end{matrix}\right)}\sum_{{q_1\geq 0,\ldots, q_k\geq 0}\atop {q_1+\cdots +q_k=m}} \frac{1}{n_1^{q_1}\cdots n_k^{q_k}}\mathrm{trace\,}\left[ \Phi_{A_1}^{q_1}\circ \cdots \circ \Phi_{A_k}^{q_k}({\Delta_{A}}(I))\right]\\
&= \lim_{q_1\to\infty}\cdots\lim_{q_k\to\infty}
\frac{\mathrm{trace\,}\left[(id-\Phi_{A_1}^{q_1+1})\circ \cdots \circ (id-\Phi_{A_k}^{q_k+1})(I)\right]}
{\prod_{i=1}^k(1+n_i+\cdots + n_i^{q_i})}\\
&=\lim_{(q_1,\ldots, q_k)\in {\mathbb Z}_+^k} \frac{1}{n_1^{q_1}\cdots n_k^{q_k}}\mathrm{trace\,}\left[ \Phi_{A_1}^{q_1}\circ \cdots \circ \Phi_{A_k}^{q_k}({\Delta_{A}}(I))\right].
\end{split}
\end{equation*}
\begin{equation*}\begin{split}
\mathrm{curv}({A})&=
\lim_{m\to\infty}\frac{1}{\left(\begin{matrix} m+k\\ k\end{matrix}\right)}\sum_{{q_1\geq 0,\ldots, q_k\geq 0}\atop {q_1+\cdots +q_k\leq m}} \frac{
\mathrm{trace\,}\left[ {K_{A}^*} (P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal H}){K_{A}}\right]}
{\mathrm{trace\,}\left[P_{(q_1,\ldots, q_k)}\right]} \\
&=
\lim_{(q_1,\ldots, q_k)\in {\mathbb Z}_+^k} \frac{
\mathrm{trace\,}\left[ {K_{A}^*} (P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal H}){K_{A}}\right]}{\mathrm{trace\,}[P_{(q_1,\ldots, q_k)}]} \\
&=\lim_{m\to\infty}\frac{1}{\left(\begin{matrix} m+k-1\\ k-1\end{matrix}\right)}\sum_{{q_1\geq 0,\ldots, q_k\geq 0}\atop {q_1+\cdots +q_k= m}}\frac{
\mathrm{trace\,}\left[ {K_{A}^*} (P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal H}){K_{A}}\right]}{\mathrm{trace\,}[P_{(q_1,\ldots, q_k)}]}\\
&=\lim_{q_1\to\infty}\cdots\lim_{q_k\to\infty}\frac{
\mathrm{trace\,}\left[ {K_{A}^*} (P_{\leq (q_1,\ldots, q_k)}\otimes I_{\mathcal H}){K_{A}}\right]}{\mathrm{trace\,}[P_{\leq (q_1,\ldots, q_k)}]}\\
&=\lim_{m\to\infty}\frac{1}{\left(\begin{matrix} m+k\\ k\end{matrix}\right)}\sum_{{q_1\geq 0,\ldots, q_k\geq 0}\atop {q_1+\cdots +q_k\leq m}}\frac {1}{n_1^{q_1}\cdots n_k^{q_k}}{\mathrm{trace\,}\left[ \Phi_{A_1}^{q_1}\circ \cdots \circ \Phi_{A_k}^{q_k}({\Delta_{A}}(I))\right]}\\
&=\lim_{m\to\infty}\frac{1}{\left(\begin{matrix} m+k-1\\ k-1\end{matrix}\right)}\sum_{{q_1\geq 0,\ldots, q_k\geq 0}\atop {q_1+\cdots +q_k=m}} \frac{1}{n_1^{q_1}\cdots n_k^{q_k}}\mathrm{trace\,}\left[ \Phi_{A_1}^{q_1}\circ \cdots \circ \Phi_{A_k}^{q_k}({\Delta_{A}}(I))\right]\\
&= \lim_{q_1\to\infty}\cdots\lim_{q_k\to\infty}
\frac{\mathrm{trace\,}\left[(id-\Phi_{A_1}^{q_1+1})\circ \cdots \circ (id-\Phi_{A_k}^{q_k+1})(I)\right]}
{\prod_{i=1}^k(1+n_i+\cdots + n_i^{q_i})}\\
&=\lim_{(q_1,\ldots, q_k)\in {\mathbb Z}_+^k} \frac{1}{n_1^{q_1}\cdots n_k^{q_k}}\mathrm{trace\,}\left[ \Phi_{A_1}^{q_1}\circ \cdots \circ \Phi_{A_k}^{q_k}({\Delta_{A}}(I))\right].
\end{split}
\end{equation*} We remark that in the particular case of the ![]() ${\mathcal U}$-twisted polydisk, i.e.
${\mathcal U}$-twisted polydisk, i.e. ![]() $n_1=\cdots =n_k=1$, we have
$n_1=\cdots =n_k=1$, we have  $\mathrm{trace\,}\left[P_{(q_1,\ldots, q_k)}\right]=1$, and therefore, the first of the assymptotic formulas for the curvature (see corollary 3.4) becomes
$\mathrm{trace\,}\left[P_{(q_1,\ldots, q_k)}\right]=1$, and therefore, the first of the assymptotic formulas for the curvature (see corollary 3.4) becomes
 \begin{equation*}
\mathrm{curv}(A)= \lim_{m\to\infty}\frac{
\mathrm{trace\,}\left[ {K_{A}^*} (P_{\leq m}\otimes I_{\mathcal H}){K_{A}}\right]}{\mathrm{trace\,} P_{\leq m}},
\end{equation*}
\begin{equation*}
\mathrm{curv}(A)= \lim_{m\to\infty}\frac{
\mathrm{trace\,}\left[ {K_{A}^*} (P_{\leq m}\otimes I_{\mathcal H}){K_{A}}\right]}{\mathrm{trace\,} P_{\leq m}},
\end{equation*} where ![]() $P_{\leq m}$ stands for the orthogonal projection of
$P_{\leq m}$ stands for the orthogonal projection of  $\ell^2({\mathbb Z}_+^k)$ onto
$\ell^2({\mathbb Z}_+^k)$ onto
Definition. Let ![]() $A:=(A_1,\ldots, A_k) $ with
$A:=(A_1,\ldots, A_k) $ with ![]() $A_i:=(A_{i,1},\ldots, A_{i,n_i})\in B({\mathcal H})^{n_i}$ and
$A_i:=(A_{i,1},\ldots, A_{i,n_i})\in B({\mathcal H})^{n_i}$ and ![]() $C:=(C_1,\ldots, C_k)$ with
$C:=(C_1,\ldots, C_k)$ with ![]() $C_i:=(C_{i,1},\ldots, C_{i,n_i})\in B({\mathcal H}')^{n_i}$.
$C_i:=(C_{i,1},\ldots, C_{i,n_i})\in B({\mathcal H}')^{n_i}$.
(i) We say that A is unitarily equivalent to C if there is a unitary operator
 $\Psi:{\mathcal H}\to {\mathcal H}'$ such that
$\Psi:{\mathcal H}\to {\mathcal H}'$ such that  $
\Psi A_{i,s}=C_{i,s}\Psi$ for any
$
\Psi A_{i,s}=C_{i,s}\Psi$ for any  $i\in \{1,\ldots, k\}$ and
$i\in \{1,\ldots, k\}$ and  $s\in \{1,\ldots, n_i\}$.
$s\in \{1,\ldots, n_i\}$.(ii) If A and C are
 ${\mathcal U}$-commuting and
${\mathcal U}$-commuting and  ${\mathcal W}$-commuting, respectively, we say that
${\mathcal W}$-commuting, respectively, we say that  $(A, {\mathcal U})$ is unitarily equivalent to
$(A, {\mathcal U})$ is unitarily equivalent to  $(C, {\mathcal W})$ if there is a unitary operator
$(C, {\mathcal W})$ if there is a unitary operator  $\Psi:{\mathcal H}\to {\mathcal H}'$ such that
$\Psi:{\mathcal H}\to {\mathcal H}'$ such that
 \begin{equation*}
\Psi A_{i,s}=C_{i,s}\Psi \quad \text{and }\quad \Psi U_{i,j}(s,t)=W_{i,j}(s,t)\Psi \ \text{for any } \ (i,j,s,t)\in \Gamma.
\end{equation*}
\begin{equation*}
\Psi A_{i,s}=C_{i,s}\Psi \quad \text{and }\quad \Psi U_{i,j}(s,t)=W_{i,j}(s,t)\Psi \ \text{for any } \ (i,j,s,t)\in \Gamma.
\end{equation*}
We note that if ![]() $(A, {\mathcal U})$ is unitarily equivalent to
$(A, {\mathcal U})$ is unitarily equivalent to ![]() $(C, {\mathcal W})$, then
$(C, {\mathcal W})$, then  $A\in \textbf{B}^{\mathcal U}({\mathcal H})$ has a positive trace class defect operator
$A\in \textbf{B}^{\mathcal U}({\mathcal H})$ has a positive trace class defect operator ![]() $\Delta_A(I_{\mathcal H})$ if and only if
$\Delta_A(I_{\mathcal H})$ if and only if  $C\in \textbf{B}^{\mathcal W}({\mathcal H}')$ has a positive trace class defect operator
$C\in \textbf{B}^{\mathcal W}({\mathcal H}')$ has a positive trace class defect operator ![]() $\Delta_C(I_{{\mathcal H}'})$. Using one of the asymptotic expressions for the curvature, it is easy to see that
$\Delta_C(I_{{\mathcal H}'})$. Using one of the asymptotic expressions for the curvature, it is easy to see that ![]() $\mathrm{curv}(A)=\mathrm{curv}(C)$. Therefore, the curvature is invariant under unitary equivalence of the pairs
$\mathrm{curv}(A)=\mathrm{curv}(C)$. Therefore, the curvature is invariant under unitary equivalence of the pairs ![]() $(A, {\mathcal U})$ and
$(A, {\mathcal U})$ and ![]() $(C, {\mathcal W})$. We remark that if A and C are just unitarily equivalent, then
$(C, {\mathcal W})$. We remark that if A and C are just unitarily equivalent, then ![]() $(A, {\mathcal U})$ is not necessarily unitarily equivalent to
$(A, {\mathcal U})$ is not necessarily unitarily equivalent to ![]() $(C, {\mathcal W})$ in general.
$(C, {\mathcal W})$ in general.
Theorem 3.6 Let A and ![]() $\{A^{(p)}\}_{p\in {\mathbb N}}$ be elements in the
$\{A^{(p)}\}_{p\in {\mathbb N}}$ be elements in the ![]() ${\mathcal U}$-twisted polyball
${\mathcal U}$-twisted polyball  $\textbf{B}^{\mathcal U}({\mathcal H})$ with positive defect operators and defect spaces included in a finite dimensional subspace of
$\textbf{B}^{\mathcal U}({\mathcal H})$ with positive defect operators and defect spaces included in a finite dimensional subspace of ![]() ${\mathcal H}$. If
${\mathcal H}$. If  ${K}_{A^{(p)}}{K}^*_{{A}^{(p)}}\to K_AK_A^*$ in the weak operator topology as
${K}_{A^{(p)}}{K}^*_{{A}^{(p)}}\to K_AK_A^*$ in the weak operator topology as ![]() $p\to\infty$, then
$p\to\infty$, then
 \begin{equation*}
\limsup_{p\to\infty}\mathrm{curv}({A}^{(p)})\leq \mathrm{curv}({A}).
\end{equation*}
\begin{equation*}
\limsup_{p\to\infty}\mathrm{curv}({A}^{(p)})\leq \mathrm{curv}({A}).
\end{equation*}Proof. Let ![]() ${\mathcal K}\subset {\mathcal H}$ be a subspace with
${\mathcal K}\subset {\mathcal H}$ be a subspace with ![]() $\dim {\mathcal K} \lt \infty$ such that
$\dim {\mathcal K} \lt \infty$ such that ![]() ${\mathcal D}_A\subset {\mathcal K}$ and
${\mathcal D}_A\subset {\mathcal K}$ and ![]() ${\mathcal D}_{A^{(p)}}\subset {\mathcal K}$ for any
${\mathcal D}_{A^{(p)}}\subset {\mathcal K}$ for any ![]() $p\in {\mathbb N}$. Note that
$p\in {\mathbb N}$. Note that
 \begin{equation*}
\lim_{p\to\infty}\mathrm{trace\,}\left[ (P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal K}){K_{A^{(p)}}}{K_{A^{(p)}}^*}\right]\\
=\mathrm{trace\,}\left[ (P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal K}){K_{A }}{K_{A }^*}\right]
\end{equation*}
\begin{equation*}
\lim_{p\to\infty}\mathrm{trace\,}\left[ (P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal K}){K_{A^{(p)}}}{K_{A^{(p)}}^*}\right]\\
=\mathrm{trace\,}\left[ (P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal K}){K_{A }}{K_{A }^*}\right]
\end{equation*} for any  $(q_1,\ldots, q_k)\in {\mathbb Z}_+^k$. A close look at the proof of theorem 3.3 reveals that
$(q_1,\ldots, q_k)\in {\mathbb Z}_+^k$. A close look at the proof of theorem 3.3 reveals that
 \begin{equation*}
\begin{split}
\lim_{p\to\infty}\!\mathrm{trace\,}\!\!
\left[\Phi_{A^{(p)}_1}^{q_1}\circ \cdots \circ \Phi_{A^{(p)}_k}^{q_k} (\Delta_{A^{(p)}}(I))\right]
&\!=\!\lim_{m\to\infty}\!\mathrm{trace\,}\!\!\left[{K_{A^{(p)}}^*} (P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal K}){K_{A^{(p)}}}\right]\\
&=\mathrm{trace\,}\left[ (P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal K}){K_{A }}{K_{A }^*}\right]\\
&=\mathrm{trace\,}\left[\Phi_{A_1}^{q_1}\circ \cdots \circ \Phi_{A_k}^{q_k} ({\Delta_{A }}(I))\right]
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
\lim_{p\to\infty}\!\mathrm{trace\,}\!\!
\left[\Phi_{A^{(p)}_1}^{q_1}\circ \cdots \circ \Phi_{A^{(p)}_k}^{q_k} (\Delta_{A^{(p)}}(I))\right]
&\!=\!\lim_{m\to\infty}\!\mathrm{trace\,}\!\!\left[{K_{A^{(p)}}^*} (P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal K}){K_{A^{(p)}}}\right]\\
&=\mathrm{trace\,}\left[ (P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal K}){K_{A }}{K_{A }^*}\right]\\
&=\mathrm{trace\,}\left[\Phi_{A_1}^{q_1}\circ \cdots \circ \Phi_{A_k}^{q_k} ({\Delta_{A }}(I))\right]
\end{split}
\end{equation*} for any  $(q_1,\ldots, q_k)\in {\mathbb Z}_+^k$. For each
$(q_1,\ldots, q_k)\in {\mathbb Z}_+^k$. For each ![]() $p\in {\mathbb N}$ and
$p\in {\mathbb N}$ and  $\textbf{q}:=(q_1,\ldots, q_k)\in {\mathbb Z}_+^k$, let
$\textbf{q}:=(q_1,\ldots, q_k)\in {\mathbb Z}_+^k$, let
 \begin{align*}
&a_\textbf{q}:=\frac{\mathrm{trace\,}\left[\Phi_{A_1}^{q_1}\circ \cdots \circ \Phi_{A_k}^{q_k} ({\Delta_{A }}(I))\right]}{n_1^{q_1}\cdots n_k^{q_k}}\quad \text{and } \\ &a_\textbf{q}^{(p)}:=
\frac{\mathrm{trace\,}
\left[\Phi_{A^{(p)}_1}^{q_1}\circ \cdots \circ \Phi_{A^{(p)}_k}^{q_k} (\Delta_{A^{(p)}}(I))\right]}{n_1^{q_1}\cdots n_k^{q_k}}.
\end{align*}
\begin{align*}
&a_\textbf{q}:=\frac{\mathrm{trace\,}\left[\Phi_{A_1}^{q_1}\circ \cdots \circ \Phi_{A_k}^{q_k} ({\Delta_{A }}(I))\right]}{n_1^{q_1}\cdots n_k^{q_k}}\quad \text{and } \\ &a_\textbf{q}^{(p)}:=
\frac{\mathrm{trace\,}
\left[\Phi_{A^{(p)}_1}^{q_1}\circ \cdots \circ \Phi_{A^{(p)}_k}^{q_k} (\Delta_{A^{(p)}}(I))\right]}{n_1^{q_1}\cdots n_k^{q_k}}.
\end{align*} As we saw in the proof of theorem 2.5,  $\{a_\textbf{q}\}_{\textbf{q}\in {\mathbb Z}_+^k}$ and
$\{a_\textbf{q}\}_{\textbf{q}\in {\mathbb Z}_+^k}$ and  $\{a_\textbf{q}^{(p)}\}_{\textbf{q}\in {\mathbb Z}_+^k}$ are decreasing multi-sequences with respect to the indices
$\{a_\textbf{q}^{(p)}\}_{\textbf{q}\in {\mathbb Z}_+^k}$ are decreasing multi-sequences with respect to the indices ![]() $q_1,\ldots, q_k$. Setting
$q_1,\ldots, q_k$. Setting  $a:=\lim_{\textbf{q}\in {\mathbb Z}_+^k} a_\textbf{q}$ and
$a:=\lim_{\textbf{q}\in {\mathbb Z}_+^k} a_\textbf{q}$ and  $a^{(p)}:=\lim_{\textbf{q}\in {\mathbb Z}_+^k} a_\textbf{q}^{(p)}$, we prove that
$a^{(p)}:=\lim_{\textbf{q}\in {\mathbb Z}_+^k} a_\textbf{q}^{(p)}$, we prove that  $\limsup_{p\to\infty} a^{(p)}\leq a$, by contradiction. Passing to a subsequence, we may assume that there is ϵ > 0 such that
$\limsup_{p\to\infty} a^{(p)}\leq a$, by contradiction. Passing to a subsequence, we may assume that there is ϵ > 0 such that ![]() $a^{(p)}-a\geq 2\epsilon \gt 0$ for any
$a^{(p)}-a\geq 2\epsilon \gt 0$ for any ![]() $p\in {\mathbb N}$. Taking into account that
$p\in {\mathbb N}$. Taking into account that  $a:=\lim_{\textbf{q}\in {\mathbb Z}_+^k} a_\textbf{q}$, we can find
$a:=\lim_{\textbf{q}\in {\mathbb Z}_+^k} a_\textbf{q}$, we can find ![]() $N\geq 1$ such that
$N\geq 1$ such that ![]() $|a_\textbf{q}-a| \lt \epsilon$ for any
$|a_\textbf{q}-a| \lt \epsilon$ for any  $\textbf{q}=(q_1,\ldots, q_k)\in {\mathbb Z}_+^k$ with
$\textbf{q}=(q_1,\ldots, q_k)\in {\mathbb Z}_+^k$ with ![]() $q_i\geq N$. Consequently,
$q_i\geq N$. Consequently,  $a_\textbf{q}^{(p)}\geq a^{(p)}$ and
$a_\textbf{q}^{(p)}\geq a^{(p)}$ and
 \begin{equation*}
|a_\textbf{q}^{(p)}-a_\textbf{q}|\geq
|a_\textbf{q}^{(p)} -a|-|a_\textbf{q} -a |\geq 2\epsilon-\epsilon=\epsilon,
\end{equation*}
\begin{equation*}
|a_\textbf{q}^{(p)}-a_\textbf{q}|\geq
|a_\textbf{q}^{(p)} -a|-|a_\textbf{q} -a |\geq 2\epsilon-\epsilon=\epsilon,
\end{equation*} which contradicts that  $\lim_{p\to\infty} a_\textbf{q}^{(p)}=a_\textbf{q}$. Consequently, using corollary 3.4, we deduce that
$\lim_{p\to\infty} a_\textbf{q}^{(p)}=a_\textbf{q}$. Consequently, using corollary 3.4, we deduce that
 \begin{equation*}
\limsup_{p\to\infty}\mathrm{curv}({A}^{(p)})\leq \mathrm{curv}({A}).
\end{equation*}
\begin{equation*}
\limsup_{p\to\infty}\mathrm{curv}({A}^{(p)})\leq \mathrm{curv}({A}).
\end{equation*}The proof is complete.
The next result shows that the curvature invariant is upper semi-continuous.
Theorem Let A and ![]() $\{A^{(p)}\}_{p\in {\mathbb N}}$ be elements in the
$\{A^{(p)}\}_{p\in {\mathbb N}}$ be elements in the ![]() ${\mathcal U}$-twisted polyball
${\mathcal U}$-twisted polyball  $\textbf{B}^{\mathcal U}({\mathcal H})$ such that they have positive defect operators and
$\textbf{B}^{\mathcal U}({\mathcal H})$ such that they have positive defect operators and ![]() $\mathrm{rank}\, \Delta_{A^{(p)}}(I)\leq C$ for any
$\mathrm{rank}\, \Delta_{A^{(p)}}(I)\leq C$ for any ![]() $p\in {\mathbb N}$. If
$p\in {\mathbb N}$. If ![]() ${A}^{(p)}\to A$ in the norm topology as
${A}^{(p)}\to A$ in the norm topology as ![]() $p\to \infty$, then
$p\to \infty$, then
 \begin{equation*}
\limsup_{p\to\infty}\mathrm{curv}({A}^{(p)})\leq \mathrm{curv}(A).
\end{equation*}
\begin{equation*}
\limsup_{p\to\infty}\mathrm{curv}({A}^{(p)})\leq \mathrm{curv}(A).
\end{equation*}Proof. According to the proof of theorem 3.6, it suffices to show that, for any  $(q_1,\ldots, q_k)\in {\mathbb Z}_+^k$,
$(q_1,\ldots, q_k)\in {\mathbb Z}_+^k$,
 \begin{equation*}
\begin{split}
\lim_{p\to\infty}\mathrm{trace\,}
\left[\Phi_{A^{(p)}_1}^{q_1}\circ \cdots \circ \Phi_{A^{(p)}_k}^{q_k} (\Delta_{A^{(p)}}(I))\right]
=\mathrm{trace\,}\left[\Phi_{A_1}^{q_1}\circ \cdots \circ \Phi_{A_k}^{q_k} ({\Delta_{A }}(I))\right].
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
\lim_{p\to\infty}\mathrm{trace\,}
\left[\Phi_{A^{(p)}_1}^{q_1}\circ \cdots \circ \Phi_{A^{(p)}_k}^{q_k} (\Delta_{A^{(p)}}(I))\right]
=\mathrm{trace\,}\left[\Phi_{A_1}^{q_1}\circ \cdots \circ \Phi_{A_k}^{q_k} ({\Delta_{A }}(I))\right].
\end{split}
\end{equation*} Consequently, using the fact that ![]() $\mathrm{rank}\, \Delta_{A^{(p)}}(I))\leq C$,
$\mathrm{rank}\, \Delta_{A^{(p)}}(I))\leq C$, ![]() $p\in {\mathbb N}$, for some C > 0, we have
$p\in {\mathbb N}$, for some C > 0, we have
 \begin{equation*}
\begin{split}
&\left|\mathrm{trace\,}\left[
\Phi_{A^{(p)}_1}^{q_1}\circ \cdots \circ \Phi_{A^{(p)}_k}^{q_k} (\Delta_{A^{(p)}}(I))
-
\Phi_{A_1}^{q_1}\circ \cdots \circ \Phi_{A_k}^{q_k} ({\Delta_{A }}(I))\right]\right|\\
&
\leq \|\Phi_{A^{(p)}_1}^{q_1}\circ \cdots \circ \Phi_{A^{(p)}_k}^{q_k} (\Delta_{A^{(p)}}(I))
-
\Phi_{A_1}^{q_1}\circ \cdots \circ \Phi_{A_k}^{q_k} ({\Delta_{A }}(I)) \| \\
&\qquad\qquad \times
\mathrm{rank}\, \left[\Phi_{A^{(p)}_1}^{q_1}\circ \cdots \circ \Phi_{A^{(p)}_k}^{q_k} (\Delta_{A^{(p)}}(I))-\Phi_{A_1}^{q_1}\circ \cdots \circ \Phi_{A_k}^{q_k} ({\Delta_{A }}(I))\right]\\
&\leq
n_1^{q_1}\cdots n_k^{q_k} \left(\mathrm{rank}\, [{\Delta_{A^{(p)}}}(I)]+\mathrm{rank}\, [{\Delta_{A }}(I)]\right)
\|\Phi_{A^{(p)}_1}^{q_1}\circ \cdots \circ \Phi_{A^{(p)}_k}^{q_k} (\Delta_{A^{(p)}}(I))\\
&\qquad\qquad\qquad-\Phi_{A_1}^{q_1}\circ \cdots \circ \Phi_{A_k}^{q_k} ({\Delta_{A }}(I)) \| \\
&\leq 2C n_1^{q_1}\cdots n_k^{q_k} \|\Phi_{A^{(p)}_1}^{q_1}\circ \cdots \circ \Phi_{A^{(p)}_k}^{q_k} (\Delta_{A^{(p)}}(I))
-
\Phi_{A_1}^{q_1}\circ \cdots \circ \Phi_{A_k}^{q_k} ({\Delta_{A }}(I))\|.
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
&\left|\mathrm{trace\,}\left[
\Phi_{A^{(p)}_1}^{q_1}\circ \cdots \circ \Phi_{A^{(p)}_k}^{q_k} (\Delta_{A^{(p)}}(I))
-
\Phi_{A_1}^{q_1}\circ \cdots \circ \Phi_{A_k}^{q_k} ({\Delta_{A }}(I))\right]\right|\\
&
\leq \|\Phi_{A^{(p)}_1}^{q_1}\circ \cdots \circ \Phi_{A^{(p)}_k}^{q_k} (\Delta_{A^{(p)}}(I))
-
\Phi_{A_1}^{q_1}\circ \cdots \circ \Phi_{A_k}^{q_k} ({\Delta_{A }}(I)) \| \\
&\qquad\qquad \times
\mathrm{rank}\, \left[\Phi_{A^{(p)}_1}^{q_1}\circ \cdots \circ \Phi_{A^{(p)}_k}^{q_k} (\Delta_{A^{(p)}}(I))-\Phi_{A_1}^{q_1}\circ \cdots \circ \Phi_{A_k}^{q_k} ({\Delta_{A }}(I))\right]\\
&\leq
n_1^{q_1}\cdots n_k^{q_k} \left(\mathrm{rank}\, [{\Delta_{A^{(p)}}}(I)]+\mathrm{rank}\, [{\Delta_{A }}(I)]\right)
\|\Phi_{A^{(p)}_1}^{q_1}\circ \cdots \circ \Phi_{A^{(p)}_k}^{q_k} (\Delta_{A^{(p)}}(I))\\
&\qquad\qquad\qquad-\Phi_{A_1}^{q_1}\circ \cdots \circ \Phi_{A_k}^{q_k} ({\Delta_{A }}(I)) \| \\
&\leq 2C n_1^{q_1}\cdots n_k^{q_k} \|\Phi_{A^{(p)}_1}^{q_1}\circ \cdots \circ \Phi_{A^{(p)}_k}^{q_k} (\Delta_{A^{(p)}}(I))
-
\Phi_{A_1}^{q_1}\circ \cdots \circ \Phi_{A_k}^{q_k} ({\Delta_{A }}(I))\|.
\end{split}
\end{equation*} Since ![]() $A^{(p)}\to {A}$ in the norm topology as
$A^{(p)}\to {A}$ in the norm topology as ![]() $p\to \infty$, it is clear that the later expression converges to 0. The rest of the proof is similar to that of theorem 3.6. The proof is complete.
$p\to \infty$, it is clear that the later expression converges to 0. The rest of the proof is similar to that of theorem 3.6. The proof is complete.
4. The  ${\mathcal U}$-twisted multi-shifts as universal operator models
${\mathcal U}$-twisted multi-shifts as universal operator models
In [Reference Popescu28], we proved the following classification result for the pure elements in the regular ![]() ${\mathcal U}$-twisted polyball having defect operators of finite rank. Let
${\mathcal U}$-twisted polyball having defect operators of finite rank. Let ![]() $A:=(A_1,\ldots, A_k)\in B({\mathcal H})^{n_1+\cdots +n_k}$ be a k-tuple with
$A:=(A_1,\ldots, A_k)\in B({\mathcal H})^{n_1+\cdots +n_k}$ be a k-tuple with ![]() $A_i:=[A_{i,1}\cdots A_{i,n_i}]$. Then, A is a pure k-tuple in the regular
$A_i:=[A_{i,1}\cdots A_{i,n_i}]$. Then, A is a pure k-tuple in the regular ![]() ${\mathcal U}$-twisted polyball, with
${\mathcal U}$-twisted polyball, with ![]() $\mathrm{rank}\, \Delta_A(I)=m$, where
$\mathrm{rank}\, \Delta_A(I)=m$, where ![]() $m\in {\mathbb N}$, if and only if there is a set
$m\in {\mathbb N}$, if and only if there is a set ![]() ${\mathcal W}:=\{W_{i,j}(s,t)\}_{(i,j,s,t)\in \Gamma}$ of commuting unitary operators on
${\mathcal W}:=\{W_{i,j}(s,t)\}_{(i,j,s,t)\in \Gamma}$ of commuting unitary operators on ![]() ${\mathbb C}^m$ with
${\mathbb C}^m$ with
and there is a jointly invariant subspace  ${\mathcal M}\subset \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathbb C}^m$ under the
${\mathcal M}\subset \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathbb C}^m$ under the ![]() $I\otimes{\mathcal W}$-twisted multi-shift
$I\otimes{\mathcal W}$-twisted multi-shift ![]() $\textbf{S}:=(\textbf{S}_1,\ldots, \textbf{S}_k)$ with
$\textbf{S}:=(\textbf{S}_1,\ldots, \textbf{S}_k)$ with ![]() $\textbf{S}_i:=[\textbf{S}_{i,1}\cdots \textbf{S}_{i,n_i}]$ and under
$\textbf{S}_i:=[\textbf{S}_{i,1}\cdots \textbf{S}_{i,n_i}]$ and under ![]() $I\otimes W_{i,j}(s,t)$ such that
$I\otimes W_{i,j}(s,t)$ such that ![]() $\dim [(P_{\mathbb C}\otimes I_{{\mathbb C}^m}){\mathcal M}^\perp]=m$ and, up to a unitary equivalence,
$\dim [(P_{\mathbb C}\otimes I_{{\mathbb C}^m}){\mathcal M}^\perp]=m$ and, up to a unitary equivalence,
Due to the spectral theorem, since ![]() $W_{i,j}(s,t)$ are commuting unitary operators on
$W_{i,j}(s,t)$ are commuting unitary operators on ![]() ${\mathbb C}^m$, there is an orthonormal basis
${\mathbb C}^m$, there is an orthonormal basis ![]() $\{v_1,\ldots,v_m\}$ of
$\{v_1,\ldots,v_m\}$ of ![]() ${\mathbb C}^m$ that simultaneously diagonalizes each
${\mathbb C}^m$ that simultaneously diagonalizes each ![]() $W_{i,j}(s,t)$, i.e.
$W_{i,j}(s,t)$, i.e.
 \begin{equation*}
W_{i,j}(s,t)v_p=z^{(p)}_{i,j}(s,t)v_p,\qquad z^{(p)}_{i,j}(s,t)\in {\mathbb T},
\end{equation*}
\begin{equation*}
W_{i,j}(s,t)v_p=z^{(p)}_{i,j}(s,t)v_p,\qquad z^{(p)}_{i,j}(s,t)\in {\mathbb T},
\end{equation*} for any ![]() $(i,j,s,t)\in \Gamma$ and
$(i,j,s,t)\in \Gamma$ and ![]() $p\in \{1,\ldots, m\}$. Setting
$p\in \{1,\ldots, m\}$. Setting  $\textbf{z}^{(p)}:=(z^{(p)}_{i,j}(s,t))_{(i,j,s,t)\in \Gamma}$, it is clear that each
$\textbf{z}^{(p)}:=(z^{(p)}_{i,j}(s,t))_{(i,j,s,t)\in \Gamma}$, it is clear that each ![]() ${\mathbb C} v_p$ is a reducing subspace for all
${\mathbb C} v_p$ is a reducing subspace for all ![]() $W_{i,j}(s,t)$ and
$W_{i,j}(s,t)$ and  $W_{i,j}(s,t)|_{{\mathbb C} v_p}=z^{(p)}_{i,j}(s,t) I_{{\mathbb C} v_p}$. Consequently, due to the definition of the multi-shift, we have
$W_{i,j}(s,t)|_{{\mathbb C} v_p}=z^{(p)}_{i,j}(s,t) I_{{\mathbb C} v_p}$. Consequently, due to the definition of the multi-shift, we have  $\textbf{S}=\bigoplus_{p=1}^m \textbf{S}_{\textbf{z}^{(p)}}$, i.e
$\textbf{S}=\bigoplus_{p=1}^m \textbf{S}_{\textbf{z}^{(p)}}$, i.e  $\textbf{S}_{i,s}=\bigoplus_{p=1}^m (\textbf{S}_{\textbf{z}^{(p)}})_{i,s}$. Therefore, the
$\textbf{S}_{i,s}=\bigoplus_{p=1}^m (\textbf{S}_{\textbf{z}^{(p)}})_{i,s}$. Therefore, the ![]() $I\otimes{\mathcal W}$-twisted multi-shift S is a direct sum of multi-shifts
$I\otimes{\mathcal W}$-twisted multi-shift S is a direct sum of multi-shifts  $\textbf{S}_\textbf{z}\in B(\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+))$ with scalar weights
$\textbf{S}_\textbf{z}\in B(\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+))$ with scalar weights ![]() $\textbf{z}=(z_{i,j}(s,t))_{(i,j,s,t)\in \Gamma}$, where
$\textbf{z}=(z_{i,j}(s,t))_{(i,j,s,t)\in \Gamma}$, where ![]() $z_{i,j}(s,t)\in {\mathbb T}$ and
$z_{i,j}(s,t)\in {\mathbb T}$ and  $z_{j,i}(t,s)=\overline{z_{i,j}(s,t})$ for
$z_{j,i}(t,s)=\overline{z_{i,j}(s,t})$ for ![]() $(i,j,s,t)\in \Gamma$.
$(i,j,s,t)\in \Gamma$.
In particular, according to Corollary 3.5 from [Reference Popescu28], A is a pure k-tuple in the regular ![]() ${\mathcal U}$-twisted polyball, with
${\mathcal U}$-twisted polyball, with ![]() $\mathrm{rank}\, \Delta_A(I)=1$ if and only if there is a set
$\mathrm{rank}\, \Delta_A(I)=1$ if and only if there is a set ![]() $\textbf{z}=(z_{i,j}(s,t))_{(i,j,s,t)\in \Gamma}$ of complex numbers in the torus
$\textbf{z}=(z_{i,j}(s,t))_{(i,j,s,t)\in \Gamma}$ of complex numbers in the torus ![]() ${\mathbb T}$ with
${\mathbb T}$ with
 \begin{equation*}
z_{j,i}(t,s)=\overline{z_{i,j}(s,t)},\qquad (i,j,s,t)\in \Gamma,
\end{equation*}
\begin{equation*}
z_{j,i}(t,s)=\overline{z_{i,j}(s,t)},\qquad (i,j,s,t)\in \Gamma,
\end{equation*} and a jointly invariant subspace  ${\mathcal M}\subset \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)$ under the standard multi-shift
${\mathcal M}\subset \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)$ under the standard multi-shift ![]() $\textbf{S}_\textbf{z}$ such that
$\textbf{S}_\textbf{z}$ such that ![]() $\dim [P_{\mathbb C}{\mathcal M}^\perp]=1$ and, up to a unitary equivalence,
$\dim [P_{\mathbb C}{\mathcal M}^\perp]=1$ and, up to a unitary equivalence,
If ![]() ${\mathcal M}'$ is another jointly co-invariant subspace under
${\mathcal M}'$ is another jointly co-invariant subspace under ![]() $(\textbf{S}_\textbf{z})_{i,s}$, then
$(\textbf{S}_\textbf{z})_{i,s}$, then ![]() $
P_{{\mathcal M}^\perp} \textbf{S}_\textbf{z}|_{{\mathcal M}^\perp}$ and
$
P_{{\mathcal M}^\perp} \textbf{S}_\textbf{z}|_{{\mathcal M}^\perp}$ and  $P_{{{\mathcal M}'}^\perp} \textbf{S}_\textbf{z}|_{{{\mathcal M}'}^\perp} $ are unitarily equivalent if and only if
$P_{{{\mathcal M}'}^\perp} \textbf{S}_\textbf{z}|_{{{\mathcal M}'}^\perp} $ are unitarily equivalent if and only if ![]() ${\mathcal M}^{\perp}={{\mathcal M}'}^\perp$. As a consequence of the next result, we deduce that if
${\mathcal M}^{\perp}={{\mathcal M}'}^\perp$. As a consequence of the next result, we deduce that if ![]() $\textbf{S}_\textbf{z}$ and
$\textbf{S}_\textbf{z}$ and ![]() ${\textbf{S}}_\textbf{z}\prime$ are the standard multi-shifts associated with the scalar weights z and
${\textbf{S}}_\textbf{z}\prime$ are the standard multi-shifts associated with the scalar weights z and ![]() $\textbf{z}\prime$, respectively,
$\textbf{z}\prime$, respectively, ![]() $\textbf{S}_\textbf{z}$ is unitarily equivalent
$\textbf{S}_\textbf{z}$ is unitarily equivalent ![]() ${\textbf{S}}_\textbf{z}\prime$ if and only if
${\textbf{S}}_\textbf{z}\prime$ if and only if ![]() $\textbf{z}=\textbf{z}\prime$.
$\textbf{z}=\textbf{z}\prime$.
Theorem 4.1 Let ![]() $\textbf{S}_{\mathcal U}$ and
$\textbf{S}_{\mathcal U}$ and ![]() $\textbf{S}_{{\mathcal U}'}$ be the standard multi-shifts associated with
$\textbf{S}_{{\mathcal U}'}$ be the standard multi-shifts associated with ![]() ${\mathcal U}\subset B({\mathcal H})$ and
${\mathcal U}\subset B({\mathcal H})$ and ![]() ${\mathcal U}'\subset B({\mathcal H}')$, respectively. Then,
${\mathcal U}'\subset B({\mathcal H}')$, respectively. Then, ![]() $\textbf{S}_{\mathcal U}$ is jointly similar to
$\textbf{S}_{\mathcal U}$ is jointly similar to ![]() $\textbf{S}_{{\mathcal U}'}$ if and only if there is an invertible operator
$\textbf{S}_{{\mathcal U}'}$ if and only if there is an invertible operator ![]() $W\in B({\mathcal H},{\mathcal H}')$ such that
$W\in B({\mathcal H},{\mathcal H}')$ such that  $U_{i,j}(s,t)=W^{-1}U_{i,j}'(s,t)W$ for any
$U_{i,j}(s,t)=W^{-1}U_{i,j}'(s,t)W$ for any ![]() $(i,j,s,t)\in \Gamma$.
$(i,j,s,t)\in \Gamma$.
Moreover, ![]() $\textbf{S}_{\mathcal U}$ is unitarily equivalent
$\textbf{S}_{\mathcal U}$ is unitarily equivalent ![]() $\textbf{S}_{{\mathcal U}'}$ if and only if there is a unitary operator
$\textbf{S}_{{\mathcal U}'}$ if and only if there is a unitary operator ![]() $W\in B({\mathcal H},{\mathcal H}')$ such that
$W\in B({\mathcal H},{\mathcal H}')$ such that ![]() $U_{i,j}(s,t)=W^*U_{i,j}'(s,t)W$.
$U_{i,j}(s,t)=W^*U_{i,j}'(s,t)W$.
Proof. Let ![]() $\{\chi_{\bf\alpha}\}_{\bf\alpha} $ with
$\{\chi_{\bf\alpha}\}_{\bf\alpha} $ with  $\bf\alpha:=(\alpha_1,\ldots, \alpha_k)\in {\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+$ be the orthonormal basis for the Hilbert space
$\bf\alpha:=(\alpha_1,\ldots, \alpha_k)\in {\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+$ be the orthonormal basis for the Hilbert space  $\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)$. Recall that
$\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)$. Recall that ![]() $\textbf{S}_{\mathcal U}=((\textbf{S}_{\mathcal U})_1,\ldots, (\textbf{S}_{\mathcal U})_k)$ with
$\textbf{S}_{\mathcal U}=((\textbf{S}_{\mathcal U})_1,\ldots, (\textbf{S}_{\mathcal U})_k)$ with ![]() $(\textbf{S}_{\mathcal U})_i:=[(\textbf{S}_{\mathcal U})_{i,1}\cdots (\textbf{S}_{\mathcal U})_{i,n_i}]$, where
$(\textbf{S}_{\mathcal U})_i:=[(\textbf{S}_{\mathcal U})_{i,1}\cdots (\textbf{S}_{\mathcal U})_{i,n_i}]$, where
 \begin{equation*}
\begin{split}
&(\textbf{S}_{\mathcal U})_{i,s}\left( \chi_{(\alpha_1,\ldots, \alpha_k)}\otimes h\right)\\
&\qquad \qquad :=\begin{cases} \chi_{(g_s^i\alpha_1,\alpha_2,\ldots, \alpha_k)}\otimes h, &\quad \text{if } i=1\\
\chi_{(\alpha_1,\ldots, \alpha_{i-1}, g_s^i \alpha_i, \alpha_{i+1},\ldots, \alpha_k)}\otimes \bf U_{i,1}(s,\alpha_1)\cdots \\ \qquad\bf U_{i,i-1}(s,\alpha_{i-1}) h,&\quad \text{if } i\in \{2,\ldots,k\}
\end{cases}
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
&(\textbf{S}_{\mathcal U})_{i,s}\left( \chi_{(\alpha_1,\ldots, \alpha_k)}\otimes h\right)\\
&\qquad \qquad :=\begin{cases} \chi_{(g_s^i\alpha_1,\alpha_2,\ldots, \alpha_k)}\otimes h, &\quad \text{if } i=1\\
\chi_{(\alpha_1,\ldots, \alpha_{i-1}, g_s^i \alpha_i, \alpha_{i+1},\ldots, \alpha_k)}\otimes \bf U_{i,1}(s,\alpha_1)\cdots \\ \qquad\bf U_{i,i-1}(s,\alpha_{i-1}) h,&\quad \text{if } i\in \{2,\ldots,k\}
\end{cases}
\end{split}
\end{equation*} for any ![]() $h\in {\mathcal H}$,
$h\in {\mathcal H}$,  $\alpha_1\in {\mathbb F}_{n_1}^+,\ldots, \alpha_{k}\in {\mathbb F}_{n_{k}}^+$, where
$\alpha_1\in {\mathbb F}_{n_1}^+,\ldots, \alpha_{k}\in {\mathbb F}_{n_{k}}^+$, where
 \begin{equation*}
\bf U_{i,j}(s, \beta)
:= \begin{cases}\prod_{b=1}^q U_{i,j}(s,j_b)&\quad \text{if }
\beta=g_{j_1}^j\cdots g_{j_q}^j\in {\mathbb F}_{n_j}^+ \\
I& \quad \text{if } \beta=g_0^j
\end{cases}
\end{equation*}
\begin{equation*}
\bf U_{i,j}(s, \beta)
:= \begin{cases}\prod_{b=1}^q U_{i,j}(s,j_b)&\quad \text{if }
\beta=g_{j_1}^j\cdots g_{j_q}^j\in {\mathbb F}_{n_j}^+ \\
I& \quad \text{if } \beta=g_0^j
\end{cases}
\end{equation*} for any ![]() $j\in \{1,\ldots, k\}$.
$j\in \{1,\ldots, k\}$.
Assume that there is an invertible operator  $X\in \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal H}\to \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal H}' $ such that
$X\in \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal H}\to \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal H}' $ such that
for any ![]() $i\in \{1,\ldots, k\}$ and
$i\in \{1,\ldots, k\}$ and ![]() $s\in \{1,\ldots, n_i\}$. Let
$s\in \{1,\ldots, n_i\}$. Let  $[X_{\bf\alpha,\bf\beta}]_{\bf\alpha,\bf\beta\in {\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+}$ be the operator block matrix of X, where
$[X_{\bf\alpha,\bf\beta}]_{\bf\alpha,\bf\beta\in {\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+}$ be the operator block matrix of X, where ![]() $\left \lt X_{\bf\alpha,\bf\beta}h,h'\right \gt =\left \lt X (\chi_{\bf\beta}\otimes h, \chi_{\bf\alpha}\otimes h'\right \gt $ for any
$\left \lt X_{\bf\alpha,\bf\beta}h,h'\right \gt =\left \lt X (\chi_{\bf\beta}\otimes h, \chi_{\bf\alpha}\otimes h'\right \gt $ for any ![]() $h\in {\mathcal H}$ and
$h\in {\mathcal H}$ and ![]() $h'\in {\mathcal H}'$. Note that
$h'\in {\mathcal H}'$. Note that
 \begin{equation*}
\begin{split}
\left \lt X(\textbf{S}_{\mathcal U})_{1,s}(\chi_{\bf\alpha}\otimes h), (\chi_{\bf\beta}\otimes h')\right \gt &=\left \lt X(\chi_{(g^1_s\alpha_1,\ldots, \alpha_k)}\otimes h), (\chi_{(\beta_1,\ldots, \beta_k)}\otimes h')\right \gt \\
&= \left \lt X_{(\beta_1,\ldots, \beta_k), (g^1_s\alpha_1,\ldots, \alpha_k)}h, h'\right \gt \end{split}
\end{equation*}
\begin{equation*}
\begin{split}
\left \lt X(\textbf{S}_{\mathcal U})_{1,s}(\chi_{\bf\alpha}\otimes h), (\chi_{\bf\beta}\otimes h')\right \gt &=\left \lt X(\chi_{(g^1_s\alpha_1,\ldots, \alpha_k)}\otimes h), (\chi_{(\beta_1,\ldots, \beta_k)}\otimes h')\right \gt \\
&= \left \lt X_{(\beta_1,\ldots, \beta_k), (g^1_s\alpha_1,\ldots, \alpha_k)}h, h'\right \gt \end{split}
\end{equation*}and
 \begin{equation*}
\begin{split}
&\left \lt (\textbf{S}_{{\mathcal U}'})_{1,s} X(\chi_{\bf\alpha}\otimes h), (\chi_{\bf\beta}\otimes h')\right \gt \\
&=\left \lt X(\chi_{\bf\alpha}\otimes h), (\textbf{S}_{{\mathcal U}'})_{1,s}^*(\chi_{\bf\beta}\otimes h')\right \gt \\
&=\begin{cases} \left \lt X(\chi_{(\alpha_1,\ldots, \alpha_k)}\otimes h), (\chi_{(\gamma_1,\beta_2,\ldots, \beta_k)}\otimes h')\right \gt &\quad \text{if } \beta_1=g^1_s \gamma_1 \text{ for some } \gamma_1\in {\mathbb F}_{n_1}^+\\
0&\quad \text{otherwise }
\end{cases}\\
&=
\begin{cases}
X_{(\gamma_1,\beta_2,\ldots, \beta_k), (\alpha_1,\ldots, \alpha_k)}&\quad \text{if } \beta_1=g^1_s \gamma_1 \text{ for some } \gamma_1\in {\mathbb F}_{n_1}^+\\
0&\quad \text{otherwise}.
\end{cases}
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
&\left \lt (\textbf{S}_{{\mathcal U}'})_{1,s} X(\chi_{\bf\alpha}\otimes h), (\chi_{\bf\beta}\otimes h')\right \gt \\
&=\left \lt X(\chi_{\bf\alpha}\otimes h), (\textbf{S}_{{\mathcal U}'})_{1,s}^*(\chi_{\bf\beta}\otimes h')\right \gt \\
&=\begin{cases} \left \lt X(\chi_{(\alpha_1,\ldots, \alpha_k)}\otimes h), (\chi_{(\gamma_1,\beta_2,\ldots, \beta_k)}\otimes h')\right \gt &\quad \text{if } \beta_1=g^1_s \gamma_1 \text{ for some } \gamma_1\in {\mathbb F}_{n_1}^+\\
0&\quad \text{otherwise }
\end{cases}\\
&=
\begin{cases}
X_{(\gamma_1,\beta_2,\ldots, \beta_k), (\alpha_1,\ldots, \alpha_k)}&\quad \text{if } \beta_1=g^1_s \gamma_1 \text{ for some } \gamma_1\in {\mathbb F}_{n_1}^+\\
0&\quad \text{otherwise}.
\end{cases}
\end{split}
\end{equation*}Consequently, due to relation (4.1), we must have
 \begin{equation*}
X_{(g^1_s \gamma_1,\beta_2,\ldots, \beta_k), (g^1_s\sigma_1,\alpha_2, \ldots, \alpha_k)}=
X_{(\gamma_1,\beta_2,\ldots, \beta_k), (\sigma_1,\alpha_2, \ldots, \alpha_k)}, \;\;\; \gamma_1,\sigma_1\in {\mathbb F}_{n_1}^+, \alpha_i,\beta_i\in {\mathbb F}_{n_i}^+,
\end{equation*}
\begin{equation*}
X_{(g^1_s \gamma_1,\beta_2,\ldots, \beta_k), (g^1_s\sigma_1,\alpha_2, \ldots, \alpha_k)}=
X_{(\gamma_1,\beta_2,\ldots, \beta_k), (\sigma_1,\alpha_2, \ldots, \alpha_k)}, \;\;\; \gamma_1,\sigma_1\in {\mathbb F}_{n_1}^+, \alpha_i,\beta_i\in {\mathbb F}_{n_i}^+,
\end{equation*}and
 \begin{equation*}
X_{(\beta_1,\ldots, \beta_k), (\alpha_1,\ldots, \alpha_k)}=0\qquad \text{if } \ \beta_1\neq \alpha_1, \alpha_i, \beta_i\in {\mathbb F}_{n_i}^+.
\end{equation*}
\begin{equation*}
X_{(\beta_1,\ldots, \beta_k), (\alpha_1,\ldots, \alpha_k)}=0\qquad \text{if } \ \beta_1\neq \alpha_1, \alpha_i, \beta_i\in {\mathbb F}_{n_i}^+.
\end{equation*} Consequently, if ![]() $\beta_1=\alpha_1$, then
$\beta_1=\alpha_1$, then
 \begin{equation}
X_{(\beta_1,\beta_2, \ldots, \beta_k), (\alpha_1, \alpha_2, \ldots, \alpha_k)}=
X_{(g_0^1,\beta_2, \ldots, \beta_k), (g_0^1, \alpha_2, \ldots, \alpha_k)}
\end{equation}
\begin{equation}
X_{(\beta_1,\beta_2, \ldots, \beta_k), (\alpha_1, \alpha_2, \ldots, \alpha_k)}=
X_{(g_0^1,\beta_2, \ldots, \beta_k), (g_0^1, \alpha_2, \ldots, \alpha_k)}
\end{equation} for any  $\alpha_2,\beta_2\in {\mathbb F}_{n_2}^+,\ldots, \alpha_k,\beta_k\in {\mathbb F}_{n_k}^+$.
$\alpha_2,\beta_2\in {\mathbb F}_{n_2}^+,\ldots, \alpha_k,\beta_k\in {\mathbb F}_{n_k}^+$.
Now, fix ![]() $i\in \{2,\ldots, k\}$ and
$i\in \{2,\ldots, k\}$ and ![]() $t\in \{1,\ldots, n_i\}$. As above, using the definition of the standard multi-shifts, we deduce that
$t\in \{1,\ldots, n_i\}$. As above, using the definition of the standard multi-shifts, we deduce that
 \begin{equation*}
\begin{split}
&\left \lt X(\textbf{S}_{\mathcal U})_{i,t}(\chi_{\bf\alpha}\otimes h), (\chi_{\bf\beta}\otimes h')\right \gt \\
&=\left \lt X(\chi_{(\alpha_1,\ldots,\alpha_{i-1}, g^i_t\alpha_i,\alpha_{i+1},\ldots, \alpha_k)}\otimes \bf U_{i,1}(t,\alpha_1)\cdots \bf U_{i,i-1}(t,\alpha_{i-1})h), (\chi_{(\beta_1,\ldots, \beta_k)}\otimes h') \right \gt \\
&= \left \lt X_{(\beta_1,\ldots, \beta_k), (\alpha_1,\ldots,\alpha_{i-1}, g^i_t\alpha_i,\alpha_{i+1},\ldots, \alpha_k)}\bf U_{i,1}(t,\alpha_1)\cdots \bf U_{i,i-1}(t,\alpha_{i-1})h, h'\right \gt \end{split}
\end{equation*}
\begin{equation*}
\begin{split}
&\left \lt X(\textbf{S}_{\mathcal U})_{i,t}(\chi_{\bf\alpha}\otimes h), (\chi_{\bf\beta}\otimes h')\right \gt \\
&=\left \lt X(\chi_{(\alpha_1,\ldots,\alpha_{i-1}, g^i_t\alpha_i,\alpha_{i+1},\ldots, \alpha_k)}\otimes \bf U_{i,1}(t,\alpha_1)\cdots \bf U_{i,i-1}(t,\alpha_{i-1})h), (\chi_{(\beta_1,\ldots, \beta_k)}\otimes h') \right \gt \\
&= \left \lt X_{(\beta_1,\ldots, \beta_k), (\alpha_1,\ldots,\alpha_{i-1}, g^i_t\alpha_i,\alpha_{i+1},\ldots, \alpha_k)}\bf U_{i,1}(t,\alpha_1)\cdots \bf U_{i,i-1}(t,\alpha_{i-1})h, h'\right \gt \end{split}
\end{equation*}and
 \begin{equation*}
\begin{split}
&\left \lt (\textbf{S}_{{\mathcal U}'})_{i,t} X(\chi_{\bf\alpha}\otimes h), (\chi_{\bf\beta}\otimes h')\right \gt \\
&=\left \lt X(\chi_{\bf\alpha}\otimes h), (\textbf{S}_{{\mathcal U}'})_{i,t}^*(\chi_{\bf\beta}\otimes h')\right \gt \\
&=\begin{cases} \bigg \lt X(\chi_{(\alpha_1,\ldots, \alpha_k)}\otimes h),(\chi_{(\beta_1,\ldots, \beta_{i-1},\gamma_i,\beta_{i+1},\ldots, \beta_k)}\otimes \\ \qquad \bf U'_{i,1}(t,\beta_1)^*\cdots \bf U'_{i,i-1}(t,\beta_{i-1})^*h')\bigg \gt &\ \text{if } \beta_i=g^i_t \gamma_i, \gamma_i\in {\mathbb F}_{n_i}^+\\
0&\ \text{otherwise }
\end{cases}\\
&=
\begin{cases}
\bigg \lt \bf U'_{i,1}(t,\beta_1)\cdots \bf U'_{i,i-1}(t,\beta_{i-1}) \\ \qquad X_{(\beta_1,\ldots, \beta_{i-1},\gamma_i,\beta_{i+1},\ldots, \beta_k), (\alpha_1,\ldots, \alpha_k)},h'\bigg \gt &\ \text{if } \beta_i=g^i_t \gamma_i \text{with } \gamma_i\in {\mathbb F}_{n_i}^+\\
0&\ \text{otherwise}.
\end{cases}
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
&\left \lt (\textbf{S}_{{\mathcal U}'})_{i,t} X(\chi_{\bf\alpha}\otimes h), (\chi_{\bf\beta}\otimes h')\right \gt \\
&=\left \lt X(\chi_{\bf\alpha}\otimes h), (\textbf{S}_{{\mathcal U}'})_{i,t}^*(\chi_{\bf\beta}\otimes h')\right \gt \\
&=\begin{cases} \bigg \lt X(\chi_{(\alpha_1,\ldots, \alpha_k)}\otimes h),(\chi_{(\beta_1,\ldots, \beta_{i-1},\gamma_i,\beta_{i+1},\ldots, \beta_k)}\otimes \\ \qquad \bf U'_{i,1}(t,\beta_1)^*\cdots \bf U'_{i,i-1}(t,\beta_{i-1})^*h')\bigg \gt &\ \text{if } \beta_i=g^i_t \gamma_i, \gamma_i\in {\mathbb F}_{n_i}^+\\
0&\ \text{otherwise }
\end{cases}\\
&=
\begin{cases}
\bigg \lt \bf U'_{i,1}(t,\beta_1)\cdots \bf U'_{i,i-1}(t,\beta_{i-1}) \\ \qquad X_{(\beta_1,\ldots, \beta_{i-1},\gamma_i,\beta_{i+1},\ldots, \beta_k), (\alpha_1,\ldots, \alpha_k)},h'\bigg \gt &\ \text{if } \beta_i=g^i_t \gamma_i \text{with } \gamma_i\in {\mathbb F}_{n_i}^+\\
0&\ \text{otherwise}.
\end{cases}
\end{split}
\end{equation*}Now, using relation (4.1), we deduce that
 \begin{equation*}
X_{(\beta_1,\ldots, \beta_i,\ldots,\beta_k), (\alpha_1,\ldots,\alpha_i,\ldots, \alpha_k)}=0\qquad \text{if } \ \beta_i\neq \alpha_i, \alpha_j, \beta_j\in {\mathbb F}_{n_j}^+
\end{equation*}
\begin{equation*}
X_{(\beta_1,\ldots, \beta_i,\ldots,\beta_k), (\alpha_1,\ldots,\alpha_i,\ldots, \alpha_k)}=0\qquad \text{if } \ \beta_i\neq \alpha_i, \alpha_j, \beta_j\in {\mathbb F}_{n_j}^+
\end{equation*}and
 \begin{equation*}
\begin{split}
&X_{(\beta_1,\ldots, g_t^i\gamma_i,\ldots,\beta_k), (\alpha_1,\ldots, g_t^i\sigma_i,\ldots, \alpha_k)} \bf U_{i,1}(t, \alpha_1)\cdots \bf U_{i,i-1}(t, \alpha_{i-1})\\
&\qquad \qquad = \bf U'_{i,1}(t, \beta_1)\cdots \bf U'_{i,i-1}(t, \beta_{i-1})
X_{(\beta_1,\ldots, \gamma_i,\ldots,\beta_k), (\alpha_1,\ldots, \sigma_i,\ldots, \alpha_k)}.
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
&X_{(\beta_1,\ldots, g_t^i\gamma_i,\ldots,\beta_k), (\alpha_1,\ldots, g_t^i\sigma_i,\ldots, \alpha_k)} \bf U_{i,1}(t, \alpha_1)\cdots \bf U_{i,i-1}(t, \alpha_{i-1})\\
&\qquad \qquad = \bf U'_{i,1}(t, \beta_1)\cdots \bf U'_{i,i-1}(t, \beta_{i-1})
X_{(\beta_1,\ldots, \gamma_i,\ldots,\beta_k), (\alpha_1,\ldots, \sigma_i,\ldots, \alpha_k)}.
\end{split}
\end{equation*} Consequently, if ![]() $\beta_i=\alpha_i$, then
$\beta_i=\alpha_i$, then
 \begin{equation}\begin{split}
&X_{(\beta_1,\ldots, \beta_i,\ldots,\beta_k), (\alpha_1,\ldots, \alpha_i,\ldots, \alpha_k)}
\bf U_{i,1}(\beta_i, \alpha_1)\cdots \bf U_{i,i-1}(\beta_i, \alpha_{i-1})\\
&\qquad \qquad= \bf U'_{i,1}(\beta_i, \beta_1)\cdots \bf U'_{i,i-1}(\beta_i, \beta_{i-1})
X_{(\beta_1,\ldots, g_0^i,\ldots,\beta_k), (\alpha_1,\ldots, g_0^i,\ldots, \alpha_k)}
\end{split}
\end{equation}
\begin{equation}\begin{split}
&X_{(\beta_1,\ldots, \beta_i,\ldots,\beta_k), (\alpha_1,\ldots, \alpha_i,\ldots, \alpha_k)}
\bf U_{i,1}(\beta_i, \alpha_1)\cdots \bf U_{i,i-1}(\beta_i, \alpha_{i-1})\\
&\qquad \qquad= \bf U'_{i,1}(\beta_i, \beta_1)\cdots \bf U'_{i,i-1}(\beta_i, \beta_{i-1})
X_{(\beta_1,\ldots, g_0^i,\ldots,\beta_k), (\alpha_1,\ldots, g_0^i,\ldots, \alpha_k)}
\end{split}
\end{equation}where
 \begin{equation*} \bf U_{i,j}(\beta_i, \alpha_j)= \prod_{b=1}^q\bf U_{i,j}(j_b, \alpha_j)\qquad \text{if } \ \beta_i=g_{j_1}^i\cdots g_{j_q}^i\in {\mathbb F}_{n_i}^+, \alpha_j\in {\mathbb F}_{n_j}^+,
\end{equation*}
\begin{equation*} \bf U_{i,j}(\beta_i, \alpha_j)= \prod_{b=1}^q\bf U_{i,j}(j_b, \alpha_j)\qquad \text{if } \ \beta_i=g_{j_1}^i\cdots g_{j_q}^i\in {\mathbb F}_{n_i}^+, \alpha_j\in {\mathbb F}_{n_j}^+,
\end{equation*} and ![]() $ \bf U_{i,j}(\beta_i, \alpha_j)=I$ if
$ \bf U_{i,j}(\beta_i, \alpha_j)=I$ if ![]() $\beta_i=g_0^i$.
$\beta_i=g_0^i$.
Due to the above results, if there is ![]() $i\in \{1,\ldots, k\}$ such that
$i\in \{1,\ldots, k\}$ such that ![]() $\alpha_i\neq \beta_i$, then
$\alpha_i\neq \beta_i$, then ![]() $X_{(\beta_1,\ldots, \beta_k), (\alpha_1,\ldots, \alpha_k)}=0$. Therefore, the non-zero entries of the operator block matrix
$X_{(\beta_1,\ldots, \beta_k), (\alpha_1,\ldots, \alpha_k)}=0$. Therefore, the non-zero entries of the operator block matrix  $[X_{\bf\alpha,\bf\beta}]_{\bf\alpha,\bf\beta\in {\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+}$ are those on the diagonal, that is,
$[X_{\bf\alpha,\bf\beta}]_{\bf\alpha,\bf\beta\in {\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+}$ are those on the diagonal, that is, ![]() $X_{(\alpha_1,\ldots, \alpha_k), (\alpha_1,\ldots, \alpha_k)}$. Using relations (4.2) and (4.3), we deduce that
$X_{(\alpha_1,\ldots, \alpha_k), (\alpha_1,\ldots, \alpha_k)}$. Using relations (4.2) and (4.3), we deduce that
 \begin{equation}
\begin{split}
X_{(\alpha_1,\ldots, \alpha_k), (\alpha_1,\ldots, \alpha_k)}
&=X_{(g_0^1,\alpha_2,\ldots, \alpha_k), (g_0^1,\alpha_2,\ldots, \alpha_k)}
=X_{(g_0^1, g_0^2,\alpha_3,\ldots, \alpha_k), (g_0^1, g_0^2,\alpha_3,\ldots, \alpha_k)}\\
&=\cdots= X_{(g_0^1, g_0^2, \ldots, g_0^k), (g_0^1, g_0^2,\ldots, g_0^k)}
\end{split}
\end{equation}
\begin{equation}
\begin{split}
X_{(\alpha_1,\ldots, \alpha_k), (\alpha_1,\ldots, \alpha_k)}
&=X_{(g_0^1,\alpha_2,\ldots, \alpha_k), (g_0^1,\alpha_2,\ldots, \alpha_k)}
=X_{(g_0^1, g_0^2,\alpha_3,\ldots, \alpha_k), (g_0^1, g_0^2,\alpha_3,\ldots, \alpha_k)}\\
&=\cdots= X_{(g_0^1, g_0^2, \ldots, g_0^k), (g_0^1, g_0^2,\ldots, g_0^k)}
\end{split}
\end{equation} for any  $\alpha_i\in {\mathbb F}_{n_i}^+$. Since X is a an invertible operator,
$\alpha_i\in {\mathbb F}_{n_i}^+$. Since X is a an invertible operator,  $X_{(g_0^1, \ldots, g_0^k), (g_0^1, \ldots, g_0^k)}\in B({\mathcal H},{\mathcal H}') $ must be invertible as well.
$X_{(g_0^1, \ldots, g_0^k), (g_0^1, \ldots, g_0^k)}\in B({\mathcal H},{\mathcal H}') $ must be invertible as well.
Now, let ![]() $i\in \{2,\ldots, k\}$ and let
$i\in \{2,\ldots, k\}$ and let ![]() $j\in \{1,\ldots, k-1\}$ be such that i > j. In what follows, we show that
$j\in \{1,\ldots, k-1\}$ be such that i > j. In what follows, we show that  $\bf U_{i,j}(s,t)=\bf U'_{i,j}(s,t)$ for any
$\bf U_{i,j}(s,t)=\bf U'_{i,j}(s,t)$ for any ![]() $s\in \{1,\ldots, n_i\}$ and
$s\in \{1,\ldots, n_i\}$ and ![]() $t\in \{1,\ldots, n_j\}$. Indeed, take
$t\in \{1,\ldots, n_j\}$. Indeed, take ![]() $\alpha_i=g_s^i$,
$\alpha_i=g_s^i$,  $\alpha_j=g_t^j$, and
$\alpha_j=g_t^j$, and ![]() $\alpha_p=g_0^p$ for any
$\alpha_p=g_0^p$ for any ![]() $p\in \{1,\ldots, k\}$ with p ≠ i and p ≠ j. Applying relations (4.3) and (4.4), we obtain
$p\in \{1,\ldots, k\}$ with p ≠ i and p ≠ j. Applying relations (4.3) and (4.4), we obtain
 \begin{equation*}
\begin{split}
&X_{(\alpha_1,\ldots, \alpha_k), (\alpha_1,\ldots, \alpha_k)} \bf U_{i,1}(g_s^i,g_0^1)\cdots \bf U_{i,j}(g_s^i, g_t^j)\cdots \bf U_{i,i-1}(g_s^i,g_0^{i-1})
\\
&= \bf U'_{i,1}(g_s^i,g_0^1)\cdots \bf U'_{i,j}(g_s^i, g_t^j)\cdots \bf U'_{i,i-1}(g_s^i,g_0^{i-1}) \\ &\qquad
X_{(\alpha_1,\ldots,\alpha_{i-1},g_0^i,\alpha_{i+1}\ldots \alpha_k), (\alpha_1,\ldots,\alpha_{i-1},g_0^i, \alpha_{i+1},\ldots \alpha_k)},
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
&X_{(\alpha_1,\ldots, \alpha_k), (\alpha_1,\ldots, \alpha_k)} \bf U_{i,1}(g_s^i,g_0^1)\cdots \bf U_{i,j}(g_s^i, g_t^j)\cdots \bf U_{i,i-1}(g_s^i,g_0^{i-1})
\\
&= \bf U'_{i,1}(g_s^i,g_0^1)\cdots \bf U'_{i,j}(g_s^i, g_t^j)\cdots \bf U'_{i,i-1}(g_s^i,g_0^{i-1}) \\ &\qquad
X_{(\alpha_1,\ldots,\alpha_{i-1},g_0^i,\alpha_{i+1}\ldots \alpha_k), (\alpha_1,\ldots,\alpha_{i-1},g_0^i, \alpha_{i+1},\ldots \alpha_k)},
\end{split}
\end{equation*}which implies
 \begin{equation*}
X_{(\alpha_1,\ldots, \alpha_k), (\alpha_1,\ldots, \alpha_k)}{\bf U_{i,j}(s,t)}= {\bf U'_{i,j}(s,t)} X_{(g_0^1, \ldots, g_0^k), (g_0^1,\ldots, g_0^k)}.
\end{equation*}
\begin{equation*}
X_{(\alpha_1,\ldots, \alpha_k), (\alpha_1,\ldots, \alpha_k)}{\bf U_{i,j}(s,t)}= {\bf U'_{i,j}(s,t)} X_{(g_0^1, \ldots, g_0^k), (g_0^1,\ldots, g_0^k)}.
\end{equation*} Consequently, again using relation (4.4), i.e.  $X_{(\alpha_1,\ldots, \alpha_k), (\alpha_1,\ldots, \alpha_k)}=X_{(g_0^1, \ldots, g_0^k), (g_0^1,\ldots, g_0^k)}:=W$, we deduce that
$X_{(\alpha_1,\ldots, \alpha_k), (\alpha_1,\ldots, \alpha_k)}=X_{(g_0^1, \ldots, g_0^k), (g_0^1,\ldots, g_0^k)}:=W$, we deduce that  $W{\bf U_{i,j}(s,t)}= {\bf U'_{i,j}(s,t)}W$, which proves our assertion. The converse is obviously true. In a similar manner, one can show that
$W{\bf U_{i,j}(s,t)}= {\bf U'_{i,j}(s,t)}W$, which proves our assertion. The converse is obviously true. In a similar manner, one can show that ![]() $\textbf{S}_{\mathcal U}$ is unitarily equivalent
$\textbf{S}_{\mathcal U}$ is unitarily equivalent ![]() $\textbf{S}_{{\mathcal U}'}$ if and only if there is a unitary operator
$\textbf{S}_{{\mathcal U}'}$ if and only if there is a unitary operator ![]() $W\in B({\mathcal H},{\mathcal H}')$ such that
$W\in B({\mathcal H},{\mathcal H}')$ such that ![]() $U_{i,j}(s,t)=W^*U_{i,j}'(s,t)W$ for any
$U_{i,j}(s,t)=W^*U_{i,j}'(s,t)W$ for any ![]() $(i,j,s,t)\in \Gamma$. The proof is complete.
$(i,j,s,t)\in \Gamma$. The proof is complete.
Corollary 4.2. Let ![]() $\textbf{S}_\textbf{z}$ and
$\textbf{S}_\textbf{z}$ and ![]() $\textbf{S}_\textbf{z'}$ be the standard multi-shifts associated with the scalar weights z and
$\textbf{S}_\textbf{z'}$ be the standard multi-shifts associated with the scalar weights z and ![]() $\textbf{z}'$, respectively. Then,
$\textbf{z}'$, respectively. Then, ![]() $\textbf{S}_\textbf{z}$ is unitarily equivalent
$\textbf{S}_\textbf{z}$ is unitarily equivalent ![]() $\textbf{S}_\textbf{z'}$ if and only if
$\textbf{S}_\textbf{z'}$ if and only if ![]() $\textbf{z}=\textbf{z'}$.
$\textbf{z}=\textbf{z'}$.
5. Curvature operator on the  ${\mathcal U}$-twisted polyball and some classification results
${\mathcal U}$-twisted polyball and some classification results
In this section, we prove that if A is an element in the ![]() ${\mathcal U}$-twisted polyball
${\mathcal U}$-twisted polyball  $ \textbf{B}^{\mathcal U}({\mathcal H})$ which admits characteristic function
$ \textbf{B}^{\mathcal U}({\mathcal H})$ which admits characteristic function ![]() $\Theta_A$ and the defect
$\Theta_A$ and the defect ![]() $\Delta_A(I)$ is a positive finite rank operator, then we can introduce a trace class curvature operator whose trace is exactly the curvature of A. This result is used to show that the curvature invariant detects the elements in
$\Delta_A(I)$ is a positive finite rank operator, then we can introduce a trace class curvature operator whose trace is exactly the curvature of A. This result is used to show that the curvature invariant detects the elements in ![]() $B({\mathcal H})^{n_1+\cdots + n_k}$ which are unitarily equivalent to a
$B({\mathcal H})^{n_1+\cdots + n_k}$ which are unitarily equivalent to a ![]() $I\otimes{\mathcal U}$-twisted multi-shift S of finite rank defect operator and completely classify them. We also show that the curvature invariant completely classifies the finite rank Beurling type jointly invariant subspace under S and
$I\otimes{\mathcal U}$-twisted multi-shift S of finite rank defect operator and completely classify them. We also show that the curvature invariant completely classifies the finite rank Beurling type jointly invariant subspace under S and ![]() $I\otimes {\mathcal U}$.
$I\otimes {\mathcal U}$.
We recall that
 \begin{equation*}
N_{\leq (q_1,\ldots, q_k)}:=\sum_{s_i\in {\mathbb Z}_+, s_i\leq q_i} \frac{1}{n_1^{s_1}\cdots n_k^{s_k}}
P_{(s_1,\ldots, s_k)},
\end{equation*}
\begin{equation*}
N_{\leq (q_1,\ldots, q_k)}:=\sum_{s_i\in {\mathbb Z}_+, s_i\leq q_i} \frac{1}{n_1^{s_1}\cdots n_k^{s_k}}
P_{(s_1,\ldots, s_k)},
\end{equation*} where ![]() $P_{(s_1,\ldots, s_k)}$ is the orthogonal projection of
$P_{(s_1,\ldots, s_k)}$ is the orthogonal projection of  $\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)$ onto the subspace
$\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)$ onto the subspace
 \begin{equation*}
\mathrm{span}\, \{\chi_{ (\alpha_1,\ldots, \alpha_k)}: \ \alpha_i\in {\mathbb F}_{n_i}^+, |\alpha_i|=s_i\}.
\end{equation*}
\begin{equation*}
\mathrm{span}\, \{\chi_{ (\alpha_1,\ldots, \alpha_k)}: \ \alpha_i\in {\mathbb F}_{n_i}^+, |\alpha_i|=s_i\}.
\end{equation*}Theorem 5.1 Let A be an element in the ![]() ${\mathcal U}$-twisted polyball
${\mathcal U}$-twisted polyball  $ \textbf{B}^{\mathcal U}({\mathcal H})$ such that
$ \textbf{B}^{\mathcal U}({\mathcal H})$ such that ![]() $\Delta_A(I)$ is a positive trace class operator. Then,
$\Delta_A(I)$ is a positive trace class operator. Then,
 \begin{equation*}
\mathrm{curv}({A})=\lim_{(q_1,\ldots, q_k)\in {\mathbb Z}_+^k} \mathrm{trace\,}\left[ \Delta_\textbf{S}(K_A K_A^*) (N_{\leq (q_1,\ldots, q_k)}\otimes I_{\mathcal H})\right],
\end{equation*}
\begin{equation*}
\mathrm{curv}({A})=\lim_{(q_1,\ldots, q_k)\in {\mathbb Z}_+^k} \mathrm{trace\,}\left[ \Delta_\textbf{S}(K_A K_A^*) (N_{\leq (q_1,\ldots, q_k)}\otimes I_{\mathcal H})\right],
\end{equation*}where KA is the noncommutative Berezin kernel of A.
Proof. Fix ![]() $j\in \{1,\ldots, k\}$, and let
$j\in \{1,\ldots, k\}$, and let  $\alpha_j\in {\mathbb F}_{n_j}^+$ with
$\alpha_j\in {\mathbb F}_{n_j}^+$ with ![]() $|\alpha_j|=s_j\leq q_j\in {\mathbb Z}_+$. Denote by
$|\alpha_j|=s_j\leq q_j\in {\mathbb Z}_+$. Denote by  $P^{(j)}_{q_j}$ the orthogonal projection of
$P^{(j)}_{q_j}$ the orthogonal projection of  $\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)$ onto
$\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)$ onto
 \begin{equation*}
\overline{\mathrm{span}} \left\{\chi_{(\beta_1,\ldots, \beta_k)}: \ \beta_1\in {\mathbb F}_{n_1}^+,\ldots, \beta_k\in {\mathbb F}_{n_k}^+ \text{and } |\beta_j|=q_j\right\}.
\end{equation*}
\begin{equation*}
\overline{\mathrm{span}} \left\{\chi_{(\beta_1,\ldots, \beta_k)}: \ \beta_1\in {\mathbb F}_{n_1}^+,\ldots, \beta_k\in {\mathbb F}_{n_k}^+ \text{and } |\beta_j|=q_j\right\}.
\end{equation*} Using the definition of the ![]() $I\otimes {\mathcal U}$-twisted multi-shift S on
$I\otimes {\mathcal U}$-twisted multi-shift S on  $B(\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal H}$, we have
$B(\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal H}$, we have
 \begin{equation*}
\begin{split}
&\textbf{S}_{j,\alpha_j}^*(P^{(j)}_{q_j}\otimes I_{\mathcal H})( \chi_{(\beta_1,\ldots, \beta_k)}\otimes h)\\
&=
\begin{cases}
\textbf{S}_{j,\alpha_j}^*(\chi_{(\beta_1,\ldots, \beta_k)}\otimes h) &\quad \text{if } |\beta_j|=q_j\\
0, &\quad \text{otherwise}
\end{cases}
\\
&=
\begin{cases}
\chi_{(\beta_1,\ldots, \beta_{j-1}, \gamma_j, \beta_{j+1},\ldots, \beta_k)}\otimes \bf{U}_{j,1}(\alpha_j,\beta_1)^*\cdots \bf{U}_{j,j-1}(\alpha_j,\beta_{j-1})^*h,&\quad \text{if } \beta_j=\alpha_j\gamma_j\\
0, &\quad \text{otherwise}
\end{cases}
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
&\textbf{S}_{j,\alpha_j}^*(P^{(j)}_{q_j}\otimes I_{\mathcal H})( \chi_{(\beta_1,\ldots, \beta_k)}\otimes h)\\
&=
\begin{cases}
\textbf{S}_{j,\alpha_j}^*(\chi_{(\beta_1,\ldots, \beta_k)}\otimes h) &\quad \text{if } |\beta_j|=q_j\\
0, &\quad \text{otherwise}
\end{cases}
\\
&=
\begin{cases}
\chi_{(\beta_1,\ldots, \beta_{j-1}, \gamma_j, \beta_{j+1},\ldots, \beta_k)}\otimes \bf{U}_{j,1}(\alpha_j,\beta_1)^*\cdots \bf{U}_{j,j-1}(\alpha_j,\beta_{j-1})^*h,&\quad \text{if } \beta_j=\alpha_j\gamma_j\\
0, &\quad \text{otherwise}
\end{cases}
\end{split}
\end{equation*} if ![]() $j\geq 2$, where
$j\geq 2$, where
 \begin{equation*}
\textbf{U}_{j,p}(\alpha_j, \beta_p):=\prod_{b=1}^{s_j} \textbf{U}_{j,p}(j_b, \beta_p)
\end{equation*}
\begin{equation*}
\textbf{U}_{j,p}(\alpha_j, \beta_p):=\prod_{b=1}^{s_j} \textbf{U}_{j,p}(j_b, \beta_p)
\end{equation*} for each ![]() $p\in \{1,\ldots, j-1\}$,
$p\in \{1,\ldots, j-1\}$,  $\alpha_j=g_{j_1}^j\cdots g_{j_{s_j}}^j\in {\mathbb F}_{n_j}^+$ and
$\alpha_j=g_{j_1}^j\cdots g_{j_{s_j}}^j\in {\mathbb F}_{n_j}^+$ and  $\beta_p\in {\mathbb F}_{n_p}^+$. If j = 1, we have
$\beta_p\in {\mathbb F}_{n_p}^+$. If j = 1, we have
 \begin{equation*}
\begin{split}
\textbf{S}_{1,\alpha_1}^*(P^{(1)}_{q_1}\otimes I_{\mathcal H})( \chi_{(\beta_1,\ldots, \beta_k)}\otimes h) = \begin{cases}
\chi_{( \gamma_1, \beta_2,\ldots, \beta_k)}\otimes h,&\quad \text{if } \beta_1=\alpha_1\gamma_1\\
0, &\quad \text{otherwise}.
\end{cases}
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
\textbf{S}_{1,\alpha_1}^*(P^{(1)}_{q_1}\otimes I_{\mathcal H})( \chi_{(\beta_1,\ldots, \beta_k)}\otimes h) = \begin{cases}
\chi_{( \gamma_1, \beta_2,\ldots, \beta_k)}\otimes h,&\quad \text{if } \beta_1=\alpha_1\gamma_1\\
0, &\quad \text{otherwise}.
\end{cases}
\end{split}
\end{equation*} Consequently, if ![]() $j\geq 2$, we deduce that
$j\geq 2$, we deduce that
 \begin{equation*}
\begin{split}
&(P^{(j)}_{q_j-s_j}\otimes I_{\mathcal H}) \textbf{S}_{j,\alpha_j}^*( \chi_{(\beta_1,\ldots, \beta_k)}\otimes h)\\
&=
\begin{cases}
(P^{(j)}_{q_j-s_j}\otimes I_{\mathcal H})\bigg(\chi_{(\beta_1,\ldots, \beta_{j-1}, \gamma_j, \beta_{j+1},\ldots, \beta_k)}\otimes \bf{U}_{j,1}(\alpha_j,\beta_1)^*\cdots \\ \qquad \bf{U}_{j,j-1}(\alpha_j,\beta_{j-1})^*h\bigg),&\quad \text{if } \beta_j=\alpha_j\gamma_j\\
0, &\quad \text{otherwise}
\end{cases}\\
&=
\begin{cases}
\chi_{(\beta_1,\ldots, \beta_{j-1}, \gamma_j, \beta_{j+1},\ldots, \beta_k)}\otimes \bf{U}_{j,1}(\alpha_j,\beta_1)^*\cdots \bf{U}_{j,j-1}(\alpha_j,\beta_{j-1})^*h,&\quad \text{if } \beta_j=\alpha_j\gamma_j\\
0, &\quad \text{otherwise}.
\end{cases}
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
&(P^{(j)}_{q_j-s_j}\otimes I_{\mathcal H}) \textbf{S}_{j,\alpha_j}^*( \chi_{(\beta_1,\ldots, \beta_k)}\otimes h)\\
&=
\begin{cases}
(P^{(j)}_{q_j-s_j}\otimes I_{\mathcal H})\bigg(\chi_{(\beta_1,\ldots, \beta_{j-1}, \gamma_j, \beta_{j+1},\ldots, \beta_k)}\otimes \bf{U}_{j,1}(\alpha_j,\beta_1)^*\cdots \\ \qquad \bf{U}_{j,j-1}(\alpha_j,\beta_{j-1})^*h\bigg),&\quad \text{if } \beta_j=\alpha_j\gamma_j\\
0, &\quad \text{otherwise}
\end{cases}\\
&=
\begin{cases}
\chi_{(\beta_1,\ldots, \beta_{j-1}, \gamma_j, \beta_{j+1},\ldots, \beta_k)}\otimes \bf{U}_{j,1}(\alpha_j,\beta_1)^*\cdots \bf{U}_{j,j-1}(\alpha_j,\beta_{j-1})^*h,&\quad \text{if } \beta_j=\alpha_j\gamma_j\\
0, &\quad \text{otherwise}.
\end{cases}
\end{split}
\end{equation*}On the other hand, if j = 1, we have
 \begin{equation*}
(P^{(1)}_{q_1-s_1}\otimes I_{\mathcal H}) \textbf{S}_{1,\alpha_1}^*( \chi_{(\beta_1,\ldots, \beta_k)}\otimes h)=
\begin{cases}
\chi_{( \gamma_1, \beta_2,\ldots, \beta_k)}\otimes h,&\quad \text{if } \beta_1=\alpha_1\gamma_1\\
0, &\quad \text{otherwise}.
\end{cases}
\end{equation*}
\begin{equation*}
(P^{(1)}_{q_1-s_1}\otimes I_{\mathcal H}) \textbf{S}_{1,\alpha_1}^*( \chi_{(\beta_1,\ldots, \beta_k)}\otimes h)=
\begin{cases}
\chi_{( \gamma_1, \beta_2,\ldots, \beta_k)}\otimes h,&\quad \text{if } \beta_1=\alpha_1\gamma_1\\
0, &\quad \text{otherwise}.
\end{cases}
\end{equation*}The above relations imply
 \begin{equation*}
\textbf{S}_{j,\alpha_j}^*(P^{(j)}_{q_j}\otimes I_{\mathcal H})=(P^{(j)}_{q_j-s_j}\otimes I_{\mathcal H}) \textbf{S}_{j,\alpha_j}^*,
\end{equation*}
\begin{equation*}
\textbf{S}_{j,\alpha_j}^*(P^{(j)}_{q_j}\otimes I_{\mathcal H})=(P^{(j)}_{q_j-s_j}\otimes I_{\mathcal H}) \textbf{S}_{j,\alpha_j}^*,
\end{equation*} for any  $\alpha_j\in {\mathbb F}_{n_j}^+$ with
$\alpha_j\in {\mathbb F}_{n_j}^+$ with ![]() $|\alpha_j|=s_j\leq q_j\in {\mathbb Z}_+$. Since
$|\alpha_j|=s_j\leq q_j\in {\mathbb Z}_+$. Since  $P_{(s_1,\ldots, s_k)}=P^{(1)}_{s_1}\cdots P^{(k)}_{s_k}$ and taking into account that
$P_{(s_1,\ldots, s_k)}=P^{(1)}_{s_1}\cdots P^{(k)}_{s_k}$ and taking into account that  $\Phi^{* s_i}_{\textbf{S}_i}(I)=n_i^{s_i} I$, we obtain
$\Phi^{* s_i}_{\textbf{S}_i}(I)=n_i^{s_i} I$, we obtain
 \begin{equation}
\begin{split}
\Phi_{\textbf{S}_1}^{* s_1}\circ\cdots \circ \Phi_{\textbf{S}_k}^{* s_k} \left(P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal H}\right)
& =\left(P_{(q_1-s_1,\ldots, q_k-s_k)}\otimes I_{\mathcal H}\right) \Phi_{\textbf{S}_1}^{* s_1}\circ\cdots \circ \Phi_{\textbf{S}_k}^{* s_k}(I)\\
&=n_1^{s_1}\cdots n_k^{s_k} \left(P_{(q_1-s_1,\ldots, q_k-s_k)}\otimes I_{\mathcal H}\right)
\end{split}
\end{equation}
\begin{equation}
\begin{split}
\Phi_{\textbf{S}_1}^{* s_1}\circ\cdots \circ \Phi_{\textbf{S}_k}^{* s_k} \left(P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal H}\right)
& =\left(P_{(q_1-s_1,\ldots, q_k-s_k)}\otimes I_{\mathcal H}\right) \Phi_{\textbf{S}_1}^{* s_1}\circ\cdots \circ \Phi_{\textbf{S}_k}^{* s_k}(I)\\
&=n_1^{s_1}\cdots n_k^{s_k} \left(P_{(q_1-s_1,\ldots, q_k-s_k)}\otimes I_{\mathcal H}\right)
\end{split}
\end{equation} for any ![]() $s_1\leq q_1,\ldots, s_k\leq q_k$. Using proposition 2.3, we have
$s_1\leq q_1,\ldots, s_k\leq q_k$. Using proposition 2.3, we have
 \begin{equation*}
X=\sum_{s_1=0}^{\infty} \cdots \sum_{s_k=0}^{\infty}\Phi_{\textbf{S}_1}^{s_1}\circ\cdots\circ \Phi_{\textbf{S}_k}^{s_k} (\Delta_\textbf{S}(X))
\end{equation*}
\begin{equation*}
X=\sum_{s_1=0}^{\infty} \cdots \sum_{s_k=0}^{\infty}\Phi_{\textbf{S}_1}^{s_1}\circ\cdots\circ \Phi_{\textbf{S}_k}^{s_k} (\Delta_\textbf{S}(X))
\end{equation*} for any ![]() $X\in (I\otimes {\mathcal U})'$. Hence,
$X\in (I\otimes {\mathcal U})'$. Hence,
 \begin{equation*}
(P_{(q_1,\ldots, q_k)} \otimes I_{\mathcal H}) X=(P_{(q_1,\ldots, q_k)} \otimes I_{\mathcal H}) \sum_{s_1=0}^{q_1} \cdots \sum_{s_k=0}^{q_k}\Phi_{\textbf{S}_1}^{s_1}\circ\cdots\circ \Phi_{\textbf{S}_k}^{s_k} (\Delta_\textbf{S}(X)).
\end{equation*}
\begin{equation*}
(P_{(q_1,\ldots, q_k)} \otimes I_{\mathcal H}) X=(P_{(q_1,\ldots, q_k)} \otimes I_{\mathcal H}) \sum_{s_1=0}^{q_1} \cdots \sum_{s_k=0}^{q_k}\Phi_{\textbf{S}_1}^{s_1}\circ\cdots\circ \Phi_{\textbf{S}_k}^{s_k} (\Delta_\textbf{S}(X)).
\end{equation*}Now, using this relation and (5.1), we deduce that
 \begin{equation*}
\begin{split}
&\mathrm{trace\,} \left[(P_{(q_1,\ldots, q_k)} \otimes I_{\mathcal H}) X\right]\\
&=\sum_{s_1=0}^{q_1} \cdots \sum_{s_k=0}^{q_k}
\mathrm{trace\,}\\ & \qquad\left[ (P_{(q_1,\ldots, q_k)} \otimes I_{\mathcal H}) \sum_{|\alpha_1|=s_1,\ldots, |\alpha_k|=s_k} \textbf{S}_{1,\alpha_1}\cdots \textbf{S}_{k,\alpha_k }\Delta_\textbf{S}(X)\textbf{S}_{k,\alpha_k }^*\cdots
\textbf{S}_{1,\alpha_1}^*
\right]\\
&=
\sum_{s_1=0}^{q_1} \cdots \sum_{s_k=0}^{q_k}
\mathrm{trace\,}\\ & \qquad\left[ \sum_{|\alpha_1|=s_1,\ldots, |\alpha_k|=s_k}
\textbf{S}_{k,\alpha_k }^* \cdots \textbf{S}_{1,\alpha_1}^*(P_{(q_1,\ldots, q_k)} \otimes I_{\mathcal H}) \textbf{S}_{1,\alpha_1}\cdots \textbf{S}_{k,\alpha_k }\Delta_\textbf{S}(X)
\right]\\
&=
\sum_{s_1=0}^{q_1} \cdots \sum_{s_k=0}^{q_k}
\mathrm{trace\,}\left[ \Delta_\textbf{S}(X) \Phi_{\textbf{S}_k}^{* s_k}\circ\cdots \circ \Phi_{\textbf{S}_1}^{* s_1} \left(P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal H}\right)
\right]\\
&=
\mathrm{trace\,} \left[ \Delta_\textbf{S}(X) \sum_{s_1=0}^{q_1} \cdots \sum_{s_k=0}^{q_k}
n_1^{s_1}\cdots n_k^{s_k} \left(P_{(q_1-s_1,\ldots, q_k-s_k)}\otimes I_{\mathcal H}\right)\right]
\\
&=
\mathrm{trace\,} \left\{\Delta_\textbf{S}(X) \left[\left(\sum_{s_1=0}^{q_1} n_1^{s_1} P^{(1)}_{q_1-s_1}\right)\cdots \left(\sum_{s_k=0}^{q_k} n_k^{s_k} P^{(k)}_{q_k-s_k}\right)
\otimes I_{\mathcal H} \right]\right\}.
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
&\mathrm{trace\,} \left[(P_{(q_1,\ldots, q_k)} \otimes I_{\mathcal H}) X\right]\\
&=\sum_{s_1=0}^{q_1} \cdots \sum_{s_k=0}^{q_k}
\mathrm{trace\,}\\ & \qquad\left[ (P_{(q_1,\ldots, q_k)} \otimes I_{\mathcal H}) \sum_{|\alpha_1|=s_1,\ldots, |\alpha_k|=s_k} \textbf{S}_{1,\alpha_1}\cdots \textbf{S}_{k,\alpha_k }\Delta_\textbf{S}(X)\textbf{S}_{k,\alpha_k }^*\cdots
\textbf{S}_{1,\alpha_1}^*
\right]\\
&=
\sum_{s_1=0}^{q_1} \cdots \sum_{s_k=0}^{q_k}
\mathrm{trace\,}\\ & \qquad\left[ \sum_{|\alpha_1|=s_1,\ldots, |\alpha_k|=s_k}
\textbf{S}_{k,\alpha_k }^* \cdots \textbf{S}_{1,\alpha_1}^*(P_{(q_1,\ldots, q_k)} \otimes I_{\mathcal H}) \textbf{S}_{1,\alpha_1}\cdots \textbf{S}_{k,\alpha_k }\Delta_\textbf{S}(X)
\right]\\
&=
\sum_{s_1=0}^{q_1} \cdots \sum_{s_k=0}^{q_k}
\mathrm{trace\,}\left[ \Delta_\textbf{S}(X) \Phi_{\textbf{S}_k}^{* s_k}\circ\cdots \circ \Phi_{\textbf{S}_1}^{* s_1} \left(P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal H}\right)
\right]\\
&=
\mathrm{trace\,} \left[ \Delta_\textbf{S}(X) \sum_{s_1=0}^{q_1} \cdots \sum_{s_k=0}^{q_k}
n_1^{s_1}\cdots n_k^{s_k} \left(P_{(q_1-s_1,\ldots, q_k-s_k)}\otimes I_{\mathcal H}\right)\right]
\\
&=
\mathrm{trace\,} \left\{\Delta_\textbf{S}(X) \left[\left(\sum_{s_1=0}^{q_1} n_1^{s_1} P^{(1)}_{q_1-s_1}\right)\cdots \left(\sum_{s_k=0}^{q_k} n_k^{s_k} P^{(k)}_{q_k-s_k}\right)
\otimes I_{\mathcal H} \right]\right\}.
\end{split}
\end{equation*}Hence, we obtain
 \begin{equation}
\begin{split}
&\frac{\mathrm{trace\,} \left[(P_{(q_1,\ldots, q_k)} \otimes I_{\mathcal H}) X\right]}{n_1^{q_1}\cdots n_k^{q_k}}\\
&=
\mathrm{trace\,} \left\{\Delta_\textbf{S}(X) \left[\left(\sum_{s_1=0}^{q_1} \frac{1}{n_1^{s_1}} P^{(1)}_{s_1}\right)\cdots \left(\sum_{s_k=0}^{q_k} \frac{1}{n_k^{s_k}} P^{(k)}_{s_k}\right)
\otimes I_{\mathcal H} \right]\right\}\\
&=
\mathrm{trace\,} \left[ \Delta_\textbf{S}(X) \sum_{s_i\in {\mathbb Z}_+, s_i\leq q_i} \frac{1}{n_1^{s_1}\cdots n_k^{s_k}}
P_{(s_1,\ldots, s_k)}\otimes I_{\mathcal H}
\right]\\
&=\mathrm{trace\,}\left[ \Delta_\textbf{S}(X) (N_{\leq (q_1,\ldots, q_k)}\otimes I_{\mathcal H})\right]
\end{split}
\end{equation}
\begin{equation}
\begin{split}
&\frac{\mathrm{trace\,} \left[(P_{(q_1,\ldots, q_k)} \otimes I_{\mathcal H}) X\right]}{n_1^{q_1}\cdots n_k^{q_k}}\\
&=
\mathrm{trace\,} \left\{\Delta_\textbf{S}(X) \left[\left(\sum_{s_1=0}^{q_1} \frac{1}{n_1^{s_1}} P^{(1)}_{s_1}\right)\cdots \left(\sum_{s_k=0}^{q_k} \frac{1}{n_k^{s_k}} P^{(k)}_{s_k}\right)
\otimes I_{\mathcal H} \right]\right\}\\
&=
\mathrm{trace\,} \left[ \Delta_\textbf{S}(X) \sum_{s_i\in {\mathbb Z}_+, s_i\leq q_i} \frac{1}{n_1^{s_1}\cdots n_k^{s_k}}
P_{(s_1,\ldots, s_k)}\otimes I_{\mathcal H}
\right]\\
&=\mathrm{trace\,}\left[ \Delta_\textbf{S}(X) (N_{\leq (q_1,\ldots, q_k)}\otimes I_{\mathcal H})\right]
\end{split}
\end{equation} for any ![]() $X\in (I\otimes {\mathcal U})'$. Since
$X\in (I\otimes {\mathcal U})'$. Since ![]() $K_AU_{i,j}(s,t)=(I\otimes U_{i,j}(s,t))K_A$ for any
$K_AU_{i,j}(s,t)=(I\otimes U_{i,j}(s,t))K_A$ for any ![]() $(i,j,s,t)\in \Gamma$, it is clear that
$(i,j,s,t)\in \Gamma$, it is clear that ![]() $K_AK_A^*\in (I\otimes {\mathcal U})'$. Using corollary 3.4 and relation (5.2) when
$K_AK_A^*\in (I\otimes {\mathcal U})'$. Using corollary 3.4 and relation (5.2) when ![]() $X= K_AK_A^*$, we obtain
$X= K_AK_A^*$, we obtain
 \begin{equation}
\begin{split}
\mathrm{curv}({A})&=
\lim_{(q_1,\ldots, q_k)\in {\mathbb Z}_+^k} \frac{
\mathrm{trace\,}\left[ {K_{A}^*} (P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal H}){K_{A}}\right]}{\mathrm{trace\,}[P_{(q_1,\ldots, q_k)}]}\\
&= \lim_{(q_1,\ldots, q_k)\in {\mathbb Z}_+^k}\mathrm{trace\,}\left[ \Delta_\textbf{S}(K_AK_A^*) (N_{\leq (q_1,\ldots, q_k)}\otimes I_{\mathcal H})\right]. \\
\end{split}
\end{equation}
\begin{equation}
\begin{split}
\mathrm{curv}({A})&=
\lim_{(q_1,\ldots, q_k)\in {\mathbb Z}_+^k} \frac{
\mathrm{trace\,}\left[ {K_{A}^*} (P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal H}){K_{A}}\right]}{\mathrm{trace\,}[P_{(q_1,\ldots, q_k)}]}\\
&= \lim_{(q_1,\ldots, q_k)\in {\mathbb Z}_+^k}\mathrm{trace\,}\left[ \Delta_\textbf{S}(K_AK_A^*) (N_{\leq (q_1,\ldots, q_k)}\otimes I_{\mathcal H})\right]. \\
\end{split}
\end{equation}This completes the proof.
Theorem 5.2 Let ![]() $A:=(A_1,\ldots, A_k)$ be an element in the
$A:=(A_1,\ldots, A_k)$ be an element in the ![]() ${\mathcal U}$-twisted polyball
${\mathcal U}$-twisted polyball  $ \textbf{B}^{\mathcal U}({\mathcal H})$ such that
$ \textbf{B}^{\mathcal U}({\mathcal H})$ such that ![]() $\Delta_A(I)$ is a positive finite rank operator and
$\Delta_A(I)$ is a positive finite rank operator and ![]() $\Delta_\textbf{S}(I-K_A K_A^*)\geq 0$. Then, the curvature operator
$\Delta_\textbf{S}(I-K_A K_A^*)\geq 0$. Then, the curvature operator ![]() $ \Delta_\textbf{S}(K_A K_A^*) (N\otimes I_{\mathcal H}) $ is trace class and
$ \Delta_\textbf{S}(K_A K_A^*) (N\otimes I_{\mathcal H}) $ is trace class and
where
 \begin{equation*}
N:=\sum_{(s_1,\ldots, s_k)\in {\mathbb Z}_+^k} \frac{1}{n_1^{s_1}\cdots n_k^{s_k}}
P_{(s_1,\ldots, s_k)}.
\end{equation*}
\begin{equation*}
N:=\sum_{(s_1,\ldots, s_k)\in {\mathbb Z}_+^k} \frac{1}{n_1^{s_1}\cdots n_k^{s_k}}
P_{(s_1,\ldots, s_k)}.
\end{equation*}Proof. Let ![]() ${\mathcal D}_A:=\Delta_A(I){\mathcal H}$, and note that
${\mathcal D}_A:=\Delta_A(I){\mathcal H}$, and note that
 \begin{equation*}
\begin{split} \frac{
\mathrm{trace\,}\left[ {(P_{(q_1,\ldots, q_k)}\otimes I_{{\mathcal D}_A})(I-{K_{A}K_{A}^*} )}\right]}{n^{q_1}\cdots n_k^{q_k}}
&\leq \|I-{K_{A}K_{A}^*} \| \frac{
\mathrm{trace\,}\left[ {(P_{(q_1,\ldots, q_k)}\otimes I_{{\mathcal D}_A})}\right]}{n^{q_1}\cdots n_k^{q_k}}\\
&\leq \|I-{K_{A}K_{A}^*} \| \dim {\mathcal D}_A.
\end{split}
\end{equation*}
\begin{equation*}
\begin{split} \frac{
\mathrm{trace\,}\left[ {(P_{(q_1,\ldots, q_k)}\otimes I_{{\mathcal D}_A})(I-{K_{A}K_{A}^*} )}\right]}{n^{q_1}\cdots n_k^{q_k}}
&\leq \|I-{K_{A}K_{A}^*} \| \frac{
\mathrm{trace\,}\left[ {(P_{(q_1,\ldots, q_k)}\otimes I_{{\mathcal D}_A})}\right]}{n^{q_1}\cdots n_k^{q_k}}\\
&\leq \|I-{K_{A}K_{A}^*} \| \dim {\mathcal D}_A.
\end{split}
\end{equation*} Hence, and using relation (5.2) when ![]() $X:=I-K_AK_A^*\in (I\otimes{\mathcal U})'$, we obtain
$X:=I-K_AK_A^*\in (I\otimes{\mathcal U})'$, we obtain
 \begin{equation*}
\mathrm{trace\,}\left[ \Delta_\textbf{S}(I-K_AK_A^*) (N_{\leq (q_1,\ldots, q_k)}\otimes I_{\mathcal H})\right]
\leq \|I-{K_{A}K_{A}^*} \| \dim {\mathcal D}_A.
\end{equation*}
\begin{equation*}
\mathrm{trace\,}\left[ \Delta_\textbf{S}(I-K_AK_A^*) (N_{\leq (q_1,\ldots, q_k)}\otimes I_{\mathcal H})\right]
\leq \|I-{K_{A}K_{A}^*} \| \dim {\mathcal D}_A.
\end{equation*} Since ![]() $\{N_{\leq (q_1,\ldots, q_k)}\}$ is an increasing multi-sequence of positive operators converging to N, we deduce that
$\{N_{\leq (q_1,\ldots, q_k)}\}$ is an increasing multi-sequence of positive operators converging to N, we deduce that
 \begin{equation}
\begin{split}
\mathrm{trace\,}\left[ \Delta_\textbf{S}(I-K_AK_A^*) (N \otimes I_{\mathcal H})\right]
&\!=\!\! \lim_{(q_1,\ldots, q_k)\in {\mathbb Z}_+^k}\!\!\mathrm{trace\,}\!\!\left[\!\Delta_\textbf{S}(I\!-\!K_AK_A^*) (N_{\leq (q_1,\ldots, q_k)}\otimes I_{\mathcal H})\!\right] \\
&\leq \|I-{K_{A}K_{A}^*} \| \dim {\mathcal D}_A.
\end{split}
\end{equation}
\begin{equation}
\begin{split}
\mathrm{trace\,}\left[ \Delta_\textbf{S}(I-K_AK_A^*) (N \otimes I_{\mathcal H})\right]
&\!=\!\! \lim_{(q_1,\ldots, q_k)\in {\mathbb Z}_+^k}\!\!\mathrm{trace\,}\!\!\left[\!\Delta_\textbf{S}(I\!-\!K_AK_A^*) (N_{\leq (q_1,\ldots, q_k)}\otimes I_{\mathcal H})\!\right] \\
&\leq \|I-{K_{A}K_{A}^*} \| \dim {\mathcal D}_A.
\end{split}
\end{equation} Consequently, ![]() $ \Delta_\textbf{S}(I-K_AK_A^*) (N \otimes I_{\mathcal H})$ is a trace class operator. On the other hand, we have
$ \Delta_\textbf{S}(I-K_AK_A^*) (N \otimes I_{\mathcal H})$ is a trace class operator. On the other hand, we have
 \begin{equation}
\begin{split}
\mathrm{trace\,} \left[\Delta_\textbf{S}(K_AK_A^*)(N\otimes I_{\mathcal H})\right]
&= \mathrm{trace\,}[\Delta_\textbf{S}(I)(N\otimes I_{{\mathcal D}_A})]\\& \qquad- \mathrm{trace\,} \left[\Delta_\textbf{S}(I-K_AK_A^*)(N\otimes I_{{\mathcal D}_A})\right]\\
&=
\mathrm{trace\,}[P_{\mathbb C}\otimes I_{{\mathcal D}_A}]-\mathrm{trace\,} \left[\Delta_\textbf{S}(I-K_AK_A^*)(N\otimes I_{{\mathcal D}_A})\right]\\
&=\mathrm{rank}\, \Delta_A(I)-\mathrm{trace\,} \left[\Delta_\textbf{S}(I-K_AK_A^*)(N\otimes I_{{\mathcal D}_A})\right].
\end{split}
\end{equation}
\begin{equation}
\begin{split}
\mathrm{trace\,} \left[\Delta_\textbf{S}(K_AK_A^*)(N\otimes I_{\mathcal H})\right]
&= \mathrm{trace\,}[\Delta_\textbf{S}(I)(N\otimes I_{{\mathcal D}_A})]\\& \qquad- \mathrm{trace\,} \left[\Delta_\textbf{S}(I-K_AK_A^*)(N\otimes I_{{\mathcal D}_A})\right]\\
&=
\mathrm{trace\,}[P_{\mathbb C}\otimes I_{{\mathcal D}_A}]-\mathrm{trace\,} \left[\Delta_\textbf{S}(I-K_AK_A^*)(N\otimes I_{{\mathcal D}_A})\right]\\
&=\mathrm{rank}\, \Delta_A(I)-\mathrm{trace\,} \left[\Delta_\textbf{S}(I-K_AK_A^*)(N\otimes I_{{\mathcal D}_A})\right].
\end{split}
\end{equation} This shows that ![]() $ \Delta_\textbf{S}(K_AK_A^*)(N\otimes I_{\mathcal H})$ is a trace class operator. Similarly, we obtain
$ \Delta_\textbf{S}(K_AK_A^*)(N\otimes I_{\mathcal H})$ is a trace class operator. Similarly, we obtain
 \begin{equation}
\begin{split}
&\mathrm{trace\,}\left[ \Delta_\textbf{S}(K_AK_A^*)(N_{\leq (q_1,\ldots, q_k)}\otimes I_{\mathcal H})\right]\\
&\qquad =
\mathrm{rank}\, \Delta_A(I)-\mathrm{trace\,} \left[\Delta_\textbf{S}(I-K_AK_A^*)(N_{\leq (q_1,\ldots, q_k)}\otimes I_{{\mathcal D}_A})\right].
\end{split}
\end{equation}
\begin{equation}
\begin{split}
&\mathrm{trace\,}\left[ \Delta_\textbf{S}(K_AK_A^*)(N_{\leq (q_1,\ldots, q_k)}\otimes I_{\mathcal H})\right]\\
&\qquad =
\mathrm{rank}\, \Delta_A(I)-\mathrm{trace\,} \left[\Delta_\textbf{S}(I-K_AK_A^*)(N_{\leq (q_1,\ldots, q_k)}\otimes I_{{\mathcal D}_A})\right].
\end{split}
\end{equation}Using relations (5.3), (5.6), (5.4), and (5.5), we obtain
 \begin{equation*}
\begin{split}
\mathrm{curv}({A})&= \lim_{(q_1,\ldots, q_k)\in {\mathbb Z}_+^k} \mathrm{trace\,} \left[\Delta_\textbf{S}(K_AK_A^*)(N_{\leq (q_1,\ldots, q_k)}\otimes I_{\mathcal H})\right]\\
&= \mathrm{rank}\, \Delta_A(I)-
\lim_{(q_1,\ldots, q_k)\in {\mathbb Z}_+^k}\mathrm{trace\,} \left[\Delta_\textbf{S}(I-K_AK_A^*)(N_{\leq (q_1,\ldots, q_k)}\otimes I_{{\mathcal D}_A})\right]\\
&= \mathrm{rank}\, \Delta_A(I)- \mathrm{trace\,} \left[\Delta_\textbf{S}(I-K_AK_A^*)(N\otimes I_{{\mathcal D}_A})\right]\\
& = \mathrm{trace\,}\left[ \Delta_\textbf{S}(K_AK_A^*)(N\otimes I_{\mathcal H})\right].
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
\mathrm{curv}({A})&= \lim_{(q_1,\ldots, q_k)\in {\mathbb Z}_+^k} \mathrm{trace\,} \left[\Delta_\textbf{S}(K_AK_A^*)(N_{\leq (q_1,\ldots, q_k)}\otimes I_{\mathcal H})\right]\\
&= \mathrm{rank}\, \Delta_A(I)-
\lim_{(q_1,\ldots, q_k)\in {\mathbb Z}_+^k}\mathrm{trace\,} \left[\Delta_\textbf{S}(I-K_AK_A^*)(N_{\leq (q_1,\ldots, q_k)}\otimes I_{{\mathcal D}_A})\right]\\
&= \mathrm{rank}\, \Delta_A(I)- \mathrm{trace\,} \left[\Delta_\textbf{S}(I-K_AK_A^*)(N\otimes I_{{\mathcal D}_A})\right]\\
& = \mathrm{trace\,}\left[ \Delta_\textbf{S}(K_AK_A^*)(N\otimes I_{\mathcal H})\right].
\end{split}
\end{equation*}The proof is complete.
Let ![]() $\textbf{S}_{\mathcal V}$ be the standard k-tuple of doubly
$\textbf{S}_{\mathcal V}$ be the standard k-tuple of doubly ![]() $I\otimes {\mathcal V}$-commuting pure isometries on the Hilbert space
$I\otimes {\mathcal V}$-commuting pure isometries on the Hilbert space  $ \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal L}$, and let
$ \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal L}$, and let ![]() $\textbf{S}_{\mathcal W}$ be the standard k-tuple of doubly
$\textbf{S}_{\mathcal W}$ be the standard k-tuple of doubly ![]() $I\otimes {\mathcal W}$-commuting pure isometries on the Hilbert space
$I\otimes {\mathcal W}$-commuting pure isometries on the Hilbert space  $ \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal K}$. A bounded linear operator
$ \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal K}$. A bounded linear operator  $M:\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal L}\to \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal K}$ is called multi-analytic with respect to the multi-shifts
$M:\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal L}\to \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal K}$ is called multi-analytic with respect to the multi-shifts ![]() $\textbf{S}_{\mathcal V}$ and
$\textbf{S}_{\mathcal V}$ and ![]() $\textbf{S}_{\mathcal W}$ if
$\textbf{S}_{\mathcal W}$ if
and
If, in addition, M is a partial isometry, we call it an inner multi-analytic operator.
Definition. We say that an element A in the ![]() ${\mathcal U}$-twisted polyball
${\mathcal U}$-twisted polyball  $\textbf{B}^{\mathcal U}({\mathcal H})$ with
$\textbf{B}^{\mathcal U}({\mathcal H})$ with ![]() $\Delta_A(I)\geq 0$ has a characteristic function if there is a multi-analytic operator
$\Delta_A(I)\geq 0$ has a characteristic function if there is a multi-analytic operator  $\Theta_A: \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal K}\to \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal D}_A$ with respect to the multi-shifts
$\Theta_A: \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal K}\to \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal D}_A$ with respect to the multi-shifts ![]() $\textbf{ S}_{{\mathcal W}}$ and
$\textbf{ S}_{{\mathcal W}}$ and  $\textbf{S}_{{\mathcal U}|_{{\mathcal D}_A}}$ such that
$\textbf{S}_{{\mathcal U}|_{{\mathcal D}_A}}$ such that ![]() $K_AK_A^*+\Theta_A \Theta_A^*=I$.
$K_AK_A^*+\Theta_A \Theta_A^*=I$.
We remark that, since ![]() $K_AK_A^*$ is in the commutant of
$K_AK_A^*$ is in the commutant of ![]() $I\otimes {\mathcal U}$, we can apply theorem 6.1 from [Reference Popescu28], to conclude that an element
$I\otimes {\mathcal U}$, we can apply theorem 6.1 from [Reference Popescu28], to conclude that an element  $A\in \textbf{B}^{\mathcal U}({\mathcal H})$ with
$A\in \textbf{B}^{\mathcal U}({\mathcal H})$ with ![]() $\Delta_A(I)\geq 0$ has a characteristic function if and only if
$\Delta_A(I)\geq 0$ has a characteristic function if and only if ![]() $\Delta_{\textbf{S}_{\mathcal U}}(I-K_A K_A^*)\geq 0$.
$\Delta_{\textbf{S}_{\mathcal U}}(I-K_A K_A^*)\geq 0$.
Corollary 5.4. If A is an element in the ![]() ${\mathcal U}$-twisted polyball
${\mathcal U}$-twisted polyball  $ \textbf{B}^{\mathcal U}({\mathcal H})$ which has characteristic function
$ \textbf{B}^{\mathcal U}({\mathcal H})$ which has characteristic function ![]() $\Theta_A$ and finite rank defect operator
$\Theta_A$ and finite rank defect operator ![]() $\Delta_A(I)\geq 0$, then
$\Delta_A(I)\geq 0$, then
Proof. Since A has a characteristic function, there is a multi-analytic operator  $\Theta_A: \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal L}\to \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal D}_A$ such that
$\Theta_A: \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal L}\to \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal D}_A$ such that ![]() $K_AK_A^*+\Theta_A \Theta_A^*=I$. Due to theorem 5.2 and its proof, we have
$K_AK_A^*+\Theta_A \Theta_A^*=I$. Due to theorem 5.2 and its proof, we have
 \begin{equation*}
\begin{split}
\mathrm{curv}({A})&= \mathrm{rank}\, \Delta_A(I)- \mathrm{trace\,} [\Delta_\textbf{S}(I-K_AK_A^*)(N\otimes I_{{\mathcal D}_A})]\\
&=\mathrm{rank}\, \Delta_A(I)- \mathrm{trace\,} [\Delta_\textbf{S}(\Theta_A\Theta_A^*)(N\otimes I_{{\mathcal D}_A})]\\
&=\mathrm{rank}\, \Delta_A(I)- \mathrm{trace\,}[\Theta_A \Delta_\textbf{S}(I)\Theta_A^*(N\otimes I_{{\mathcal D}_A})]\\
&=\mathrm{rank}\, \Delta_A(I)-\mathrm{trace\,}[\Theta_A(P_{\mathbb C}\otimes I)\Theta_A^*(N\otimes I_{\mathcal H})].
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
\mathrm{curv}({A})&= \mathrm{rank}\, \Delta_A(I)- \mathrm{trace\,} [\Delta_\textbf{S}(I-K_AK_A^*)(N\otimes I_{{\mathcal D}_A})]\\
&=\mathrm{rank}\, \Delta_A(I)- \mathrm{trace\,} [\Delta_\textbf{S}(\Theta_A\Theta_A^*)(N\otimes I_{{\mathcal D}_A})]\\
&=\mathrm{rank}\, \Delta_A(I)- \mathrm{trace\,}[\Theta_A \Delta_\textbf{S}(I)\Theta_A^*(N\otimes I_{{\mathcal D}_A})]\\
&=\mathrm{rank}\, \Delta_A(I)-\mathrm{trace\,}[\Theta_A(P_{\mathbb C}\otimes I)\Theta_A^*(N\otimes I_{\mathcal H})].
\end{split}
\end{equation*}This completes the proof.
In what follows, we show that the curvature invariant detects the elements in ![]() $B({\mathcal H})^{n_1+\cdots + n_k}$ which are unitarily equivalent to
$B({\mathcal H})^{n_1+\cdots + n_k}$ which are unitarily equivalent to ![]() $I\otimes {\mathcal W}$-twisted multi-shifts
$I\otimes {\mathcal W}$-twisted multi-shifts ![]() $\textbf{S}_{\mathcal W}$ of finite rank defect operator, i.e. acting on
$\textbf{S}_{\mathcal W}$ of finite rank defect operator, i.e. acting on  $\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal K}$ with
$\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal K}$ with ![]() $\dim {\mathcal K} \lt \infty$.
$\dim {\mathcal K} \lt \infty$.
Theorem 5.5 Let ![]() $A\in B({\mathcal H})^{n_1+\cdots + n_k}$. Then A is unitarily equivalent to an
$A\in B({\mathcal H})^{n_1+\cdots + n_k}$. Then A is unitarily equivalent to an ![]() $I\otimes {\mathcal W}$-twisted multi-shift
$I\otimes {\mathcal W}$-twisted multi-shift ![]() $\textbf{S}_{\mathcal W}$ acting on
$\textbf{S}_{\mathcal W}$ acting on  $\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal K}$ with
$\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal K}$ with ![]() $\dim {\mathcal K} \lt \infty$ if and only if A is a pure element in a regular
$\dim {\mathcal K} \lt \infty$ if and only if A is a pure element in a regular ![]() ${\mathcal U}$-twisted polyball
${\mathcal U}$-twisted polyball  $\textbf{B}_{reg}^{\mathcal U} ({\mathcal H})$ such that A has a characteristic function and
$\textbf{B}_{reg}^{\mathcal U} ({\mathcal H})$ such that A has a characteristic function and
In this case, the noncommutative Berezin kernel  $K_A:{\mathcal H}\to \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal D}_A$ is a unitary operator and
$K_A:{\mathcal H}\to \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal D}_A$ is a unitary operator and
 \begin{equation*}
A_{i,s}=K_A^*(\textbf{S}_{{\mathcal U}|_{{\mathcal D}_A}})_{i,s} K_A
\end{equation*}
\begin{equation*}
A_{i,s}=K_A^*(\textbf{S}_{{\mathcal U}|_{{\mathcal D}_A}})_{i,s} K_A
\end{equation*} for any ![]() $i\in \{1,\ldots, k\}$ and
$i\in \{1,\ldots, k\}$ and ![]() $s\in \{1,\ldots, n_i\}$.
$s\in \{1,\ldots, n_i\}$.
Proof. Let ![]() $A\in B({\mathcal H})^{n_1+\cdots + n_k}$, and assume that A is unitarily equivalent to an
$A\in B({\mathcal H})^{n_1+\cdots + n_k}$, and assume that A is unitarily equivalent to an ![]() $I\otimes {\mathcal W}$-twisted multi-shift
$I\otimes {\mathcal W}$-twisted multi-shift ![]() $\textbf{S}_{\mathcal W}$ acting on
$\textbf{S}_{\mathcal W}$ acting on  $\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal K}$ with
$\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal K}$ with ![]() $\dim {\mathcal K} \lt \infty$. Then, there is a unitary operator
$\dim {\mathcal K} \lt \infty$. Then, there is a unitary operator  $\Psi:{\mathcal H}\to \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal K}$ such that
$\Psi:{\mathcal H}\to \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal K}$ such that ![]() $A_{i,s}=\Psi^* (\textbf{S}_{{\mathcal W}})_{i,s}\Psi$ for any
$A_{i,s}=\Psi^* (\textbf{S}_{{\mathcal W}})_{i,s}\Psi$ for any ![]() $i\in \{1,\ldots, k\}$ and
$i\in \{1,\ldots, k\}$ and ![]() $s\in \{1,\ldots, n_i\}$. Note that
$s\in \{1,\ldots, n_i\}$. Note that ![]() $\Delta_A(I)=\Psi^* \Delta_{\textbf{S}_{{\mathcal W}}}(I) \Psi\geq 0$ and
$\Delta_A(I)=\Psi^* \Delta_{\textbf{S}_{{\mathcal W}}}(I) \Psi\geq 0$ and
 \begin{equation*}
\mathrm{rank}\, \Delta_A(I)= \mathrm{rank}\, \Delta_{\textbf{S}_{{\mathcal W}}}(I)=\mathrm{rank}\, (P_{\mathbb C}\otimes I_{\mathcal K})=\dim {\mathcal K}.
\end{equation*}
\begin{equation*}
\mathrm{rank}\, \Delta_A(I)= \mathrm{rank}\, \Delta_{\textbf{S}_{{\mathcal W}}}(I)=\mathrm{rank}\, (P_{\mathbb C}\otimes I_{\mathcal K})=\dim {\mathcal K}.
\end{equation*} Since ![]() $\textbf{S}_{{\mathcal W}}$ is a pure k-tuple of row isometries which are doubly
$\textbf{S}_{{\mathcal W}}$ is a pure k-tuple of row isometries which are doubly ![]() $(I\otimes {\mathcal W})$-commuting, it is easy to see that A is a pure k-tuple of row isometries which are doubly
$(I\otimes {\mathcal W})$-commuting, it is easy to see that A is a pure k-tuple of row isometries which are doubly ![]() ${\mathcal U}$-commuting, where
${\mathcal U}$-commuting, where ![]() ${\mathcal U}=\{U_{i,j}(s,t)\}$ is defined by setting
${\mathcal U}=\{U_{i,j}(s,t)\}$ is defined by setting ![]() $U_{i,j}(s,t):=\Psi^* (I\otimes W_{i,j}(s,t))\Psi$. Therefore, A is a pure element in the regular
$U_{i,j}(s,t):=\Psi^* (I\otimes W_{i,j}(s,t))\Psi$. Therefore, A is a pure element in the regular ![]() ${\mathcal U}$-twisted polyball
${\mathcal U}$-twisted polyball  $\textbf{B}^{\mathcal U}_{reg}({\mathcal H})$. On the other hand, using the definition of the
$\textbf{B}^{\mathcal U}_{reg}({\mathcal H})$. On the other hand, using the definition of the ![]() $I\otimes {\mathcal W}$-twisted multi-shift
$I\otimes {\mathcal W}$-twisted multi-shift ![]() $\textbf{S}:=\textbf{S}_{\mathcal W}$ acting on
$\textbf{S}:=\textbf{S}_{\mathcal W}$ acting on  $\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal K}$, one can show that the noncommutative Berezin kernel
$\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal K}$, one can show that the noncommutative Berezin kernel ![]() $K_\textbf{S}$ can be identified with the identity on
$K_\textbf{S}$ can be identified with the identity on  $\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal K}$. Indeed, we have
$\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal K}$. Indeed, we have  $K_\textbf{S}: \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal K}\to \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal D}_\textbf{S}$. Under the identification of
$K_\textbf{S}: \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal K}\to \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal D}_\textbf{S}$. Under the identification of  ${\mathbb C}\chi_{(g_0^1,\ldots, g_0^k)}$ with
${\mathbb C}\chi_{(g_0^1,\ldots, g_0^k)}$ with ![]() ${\mathbb C}$, we have
${\mathbb C}$, we have ![]() $\Delta_\textbf{S}(I)=P_{\mathbb C}\otimes I_{\mathcal K}$ and
$\Delta_\textbf{S}(I)=P_{\mathbb C}\otimes I_{\mathcal K}$ and ![]() ${\mathcal D}_\textbf{S}={\mathbb C}\otimes {\mathcal K}={\mathcal K}$. Since
${\mathcal D}_\textbf{S}={\mathbb C}\otimes {\mathcal K}={\mathcal K}$. Since
 \begin{equation*}
K_\textbf{S} (\chi_{(\alpha_1,\ldots, \alpha_k)}\otimes h) :=\!\!\sum_{\beta_1\in {\mathbb F}_{n_1}^+,\ldots, \beta_k\in {\mathbb F}_{n_k}^+}\!\!
\chi_{(\beta_1,\ldots, \beta_k)}\otimes (P_{\mathbb C}\otimes I_{\mathcal K})\textbf{S}_{k,\beta_k}^*\cdots \textbf{S}_{1,\beta_1}^*(\chi_{(\alpha_1,\ldots, \alpha_k)}\otimes h),
\end{equation*}
\begin{equation*}
K_\textbf{S} (\chi_{(\alpha_1,\ldots, \alpha_k)}\otimes h) :=\!\!\sum_{\beta_1\in {\mathbb F}_{n_1}^+,\ldots, \beta_k\in {\mathbb F}_{n_k}^+}\!\!
\chi_{(\beta_1,\ldots, \beta_k)}\otimes (P_{\mathbb C}\otimes I_{\mathcal K})\textbf{S}_{k,\beta_k}^*\cdots \textbf{S}_{1,\beta_1}^*(\chi_{(\alpha_1,\ldots, \alpha_k)}\otimes h),
\end{equation*} for ![]() $h\in {\mathcal K}$, and
$h\in {\mathcal K}$, and
 \begin{equation*}
(P_{\mathbb C}\otimes I_{\mathcal K})\textbf{S}_{k,\beta_k}^*\cdots \textbf{S}_{1,\beta_1}^*(\chi_{(\alpha_1,\ldots, \alpha_k)}\otimes h)
=\begin{cases}
\chi_{(g_0^1,\ldots, g_0^k)}\otimes h,&\quad \text{if } \alpha_1=\beta_1,\ldots, \alpha_k=\beta_k
\\
0, &\quad \text{otherwise},
\end{cases}
\end{equation*}
\begin{equation*}
(P_{\mathbb C}\otimes I_{\mathcal K})\textbf{S}_{k,\beta_k}^*\cdots \textbf{S}_{1,\beta_1}^*(\chi_{(\alpha_1,\ldots, \alpha_k)}\otimes h)
=\begin{cases}
\chi_{(g_0^1,\ldots, g_0^k)}\otimes h,&\quad \text{if } \alpha_1=\beta_1,\ldots, \alpha_k=\beta_k
\\
0, &\quad \text{otherwise},
\end{cases}
\end{equation*} using the above-mentioned identification, we obtain ![]() $K_\textbf{S} (\chi_{(\alpha_1,\ldots, \alpha_k)}\otimes h) = \chi_{(\alpha_1,\ldots, \alpha_k)}\otimes h$, which proves our assertion. Now, taking into account that A is unitarily equivalent to S, Corollary 3.4 implies
$K_\textbf{S} (\chi_{(\alpha_1,\ldots, \alpha_k)}\otimes h) = \chi_{(\alpha_1,\ldots, \alpha_k)}\otimes h$, which proves our assertion. Now, taking into account that A is unitarily equivalent to S, Corollary 3.4 implies
 \begin{align*}
\mathrm{curv}(A)= & \mathrm{curv}(\textbf{S})=\lim_{q_1\to\infty}\cdots\lim_{q_k\to\infty}\frac{
\mathrm{trace\,}\left[ {K_\textbf{S}^*} (P_{\leq (q_1,\ldots, q_k)}\otimes I_{\mathcal K}){K_\textbf{S}}\right]}{\mathrm{trace\,}[P_{\leq (q_1,\ldots, q_k)}]}\\ & \qquad=\dim{\mathcal K}= \mathrm{rank}\, \Delta_A(I).
\end{align*}
\begin{align*}
\mathrm{curv}(A)= & \mathrm{curv}(\textbf{S})=\lim_{q_1\to\infty}\cdots\lim_{q_k\to\infty}\frac{
\mathrm{trace\,}\left[ {K_\textbf{S}^*} (P_{\leq (q_1,\ldots, q_k)}\otimes I_{\mathcal K}){K_\textbf{S}}\right]}{\mathrm{trace\,}[P_{\leq (q_1,\ldots, q_k)}]}\\ & \qquad=\dim{\mathcal K}= \mathrm{rank}\, \Delta_A(I).
\end{align*} On the other hand, since ![]() $K_\textbf{S} K_\textbf{S}^*=I$, we have
$K_\textbf{S} K_\textbf{S}^*=I$, we have ![]() $\Theta_\textbf{S}=0$ as a characteristic function of S. This completes the proof of the direct implication.
$\Theta_\textbf{S}=0$ as a characteristic function of S. This completes the proof of the direct implication.
To prove the converse, assume that A is a pure element in a regular ![]() ${\mathcal U}$-twisted polyball
${\mathcal U}$-twisted polyball  $\textbf{B}_{reg}^{\mathcal U} ({\mathcal H})$ such that A has a characteristic function and
$\textbf{B}_{reg}^{\mathcal U} ({\mathcal H})$ such that A has a characteristic function and ![]() $ \mathrm{curv}({A})=\mathrm{rank}\, \Delta_A(I) \lt \infty.
$ Therefore, there is a multi-analytic
$ \mathrm{curv}({A})=\mathrm{rank}\, \Delta_A(I) \lt \infty.
$ Therefore, there is a multi-analytic  $\Theta_A:\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal E}\to \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal D}_A$ with respect to the multi-shifts
$\Theta_A:\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal E}\to \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal D}_A$ with respect to the multi-shifts ![]() $\textbf{S}_{\mathcal W}$ and
$\textbf{S}_{\mathcal W}$ and  $\textbf{S}_{{\mathcal U}|_{{\mathcal D}_A}}$, i.e.
$\textbf{S}_{{\mathcal U}|_{{\mathcal D}_A}}$, i.e.
 \begin{equation*}
\Theta_A(\textbf{S}_{\mathcal W})_{i,s} =(\textbf{S}_{{\mathcal U}|_{{\mathcal D}_A}})_{i,s} \Theta_A, \qquad i\in\{1,\ldots, k\}, s\in \{1,\ldots, n_i\}
\end{equation*}
\begin{equation*}
\Theta_A(\textbf{S}_{\mathcal W})_{i,s} =(\textbf{S}_{{\mathcal U}|_{{\mathcal D}_A}})_{i,s} \Theta_A, \qquad i\in\{1,\ldots, k\}, s\in \{1,\ldots, n_i\}
\end{equation*}and
such that ![]() $K_A K_A^*+\Theta_A \Theta_A^*=I$. Since A is pure, the noncommutative Berezin kernel is an isometry and, consequently,
$K_A K_A^*+\Theta_A \Theta_A^*=I$. Since A is pure, the noncommutative Berezin kernel is an isometry and, consequently, ![]() $\Theta_A$ is a partial isometry. We remark that
$\Theta_A$ is a partial isometry. We remark that
 \begin{equation*}
\mathrm{range}\,\Theta_A^*=\left\{x\in \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal E}: \ \|\Theta_A(x)\|=\|x\|\right\}
\end{equation*}
\begin{equation*}
\mathrm{range}\,\Theta_A^*=\left\{x\in \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal E}: \ \|\Theta_A(x)\|=\|x\|\right\}
\end{equation*} is the initial space of ![]() $\Theta_A$ which is invariant under all the isometries
$\Theta_A$ which is invariant under all the isometries ![]() $(\textbf{S}_{\mathcal W})_{i,s}$, due to the fact that
$(\textbf{S}_{\mathcal W})_{i,s}$, due to the fact that  $
\Theta_A(\textbf{S}_{\mathcal W})_{i,s} =(\textbf{S}_{{\mathcal U}|_{{\mathcal D}_A}})_{i,s} \Theta_A$. Moreover, since
$
\Theta_A(\textbf{S}_{\mathcal W})_{i,s} =(\textbf{S}_{{\mathcal U}|_{{\mathcal D}_A}})_{i,s} \Theta_A$. Moreover, since  $\left(\mathrm{range}\,\Theta_A^*\right)^\perp=\ker \Theta_A$, it is clear that
$\left(\mathrm{range}\,\Theta_A^*\right)^\perp=\ker \Theta_A$, it is clear that  $\left(\mathrm{range}\,\Theta_A^*\right)^\perp$ is invariant under all isometries
$\left(\mathrm{range}\,\Theta_A^*\right)^\perp$ is invariant under all isometries ![]() $(\textbf{S}_{\mathcal W})_{i,s}$, and consequently, it is jointly reducing for these operators. Due to the fact that
$(\textbf{S}_{\mathcal W})_{i,s}$, and consequently, it is jointly reducing for these operators. Due to the fact that
the subspace  $\left(\mathrm{range}\,\Theta_A^*\right)^\perp$ is also reducing for the operators in
$\left(\mathrm{range}\,\Theta_A^*\right)^\perp$ is also reducing for the operators in ![]() $I\otimes {\mathcal W}$.
$I\otimes {\mathcal W}$.
Since the support of ![]() $\Theta_A$ is defined as the smallest reducing subspace
$\Theta_A$ is defined as the smallest reducing subspace  $\mathrm{supp}(\Theta_A)\subset \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal E}$ under the operators
$\mathrm{supp}(\Theta_A)\subset \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal E}$ under the operators ![]() $(\textbf{S}_{\mathcal W})_{i,s}$ containing the co-invariant subspace
$(\textbf{S}_{\mathcal W})_{i,s}$ containing the co-invariant subspace ![]() $\mathrm{range}\,\Theta_A^*$, we conclude that
$\mathrm{range}\,\Theta_A^*$, we conclude that ![]() $\mathrm{supp}(\Theta_A)=\mathrm{range}\,\Theta_A^*$. Note that
$\mathrm{supp}(\Theta_A)=\mathrm{range}\,\Theta_A^*$. Note that ![]() $\Phi:=\Theta_A|_{\mathrm{supp}(\Theta_A)}$ is an isometric operator and
$\Phi:=\Theta_A|_{\mathrm{supp}(\Theta_A)}$ is an isometric operator and ![]() $\Phi\Phi^*=\Theta_A\Theta_A^*$. According to theorem 3.1 from [Reference Popescu28],
$\Phi\Phi^*=\Theta_A\Theta_A^*$. According to theorem 3.1 from [Reference Popescu28],  $\mathrm{supp}(\Theta_A)=\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal L}$, where
$\mathrm{supp}(\Theta_A)=\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal L}$, where  ${\mathcal L}:=\overline{(P_{\mathbb C}\otimes I_{\mathcal E})\mathrm{range}\,\Theta_A^*}\subset {\mathcal E}$.
${\mathcal L}:=\overline{(P_{\mathbb C}\otimes I_{\mathcal E})\mathrm{range}\,\Theta_A^*}\subset {\mathcal E}$.
Since  $\Delta_{\textbf{S}_{\mathcal W}}(I):=(id-\Phi_{(\textbf{S}_{\mathcal W})_1})\circ\cdots \circ (id-\Phi_{(\textbf{S}_{\mathcal W})_k})(I)=P_{\mathbb C}\otimes I_{\mathcal E}$ and
$\Delta_{\textbf{S}_{\mathcal W}}(I):=(id-\Phi_{(\textbf{S}_{\mathcal W})_1})\circ\cdots \circ (id-\Phi_{(\textbf{S}_{\mathcal W})_k})(I)=P_{\mathbb C}\otimes I_{\mathcal E}$ and ![]() $\mathrm{range}\,\Theta_A^*$ is a reducing subspace under all unitary operators
$\mathrm{range}\,\Theta_A^*$ is a reducing subspace under all unitary operators ![]() $I\otimes W_{i,j}(s,t)$, we deduce that
$I\otimes W_{i,j}(s,t)$, we deduce that
 \begin{equation*}
\begin{split}
W_{i,j}(s,t)(P_{\mathbb C}\otimes I_{\mathcal E})\mathrm{range}\,\Theta_A^*&=(I\otimes W_{i,j}(s,t))\Delta_{\textbf{S}_{\mathcal W}}(I)\mathrm{range}\,\Theta_A^*\\
&=\Delta_{\textbf{S}_{\mathcal W}}(I)(I\otimes W_{i,j}(s,t))\mathrm{range}\,\Theta_A^*\\
&=\Delta_{\textbf{S}_{\mathcal W}}(I)\mathrm{range}\,\Theta_A^*.
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
W_{i,j}(s,t)(P_{\mathbb C}\otimes I_{\mathcal E})\mathrm{range}\,\Theta_A^*&=(I\otimes W_{i,j}(s,t))\Delta_{\textbf{S}_{\mathcal W}}(I)\mathrm{range}\,\Theta_A^*\\
&=\Delta_{\textbf{S}_{\mathcal W}}(I)(I\otimes W_{i,j}(s,t))\mathrm{range}\,\Theta_A^*\\
&=\Delta_{\textbf{S}_{\mathcal W}}(I)\mathrm{range}\,\Theta_A^*.
\end{split}
\end{equation*} Hence, the subspace ![]() ${\mathcal L}$ is reducing for all the unitaries
${\mathcal L}$ is reducing for all the unitaries ![]() $W_{i,j}(s,t)$. Since
$W_{i,j}(s,t)$. Since
 \begin{equation*}
\Theta_A(\textbf{S}_{\mathcal W})_{i,s} =(\textbf{S}_{{\mathcal U}|_{{\mathcal D}_A}})_{i,s} \Theta_A \ \text{and } \ \Theta_A(I\otimes W_{i,j}(s,t))=(I\otimes U_{i,j}(s,t)|_{{\mathcal D}_A})\Theta_A,
\end{equation*}
\begin{equation*}
\Theta_A(\textbf{S}_{\mathcal W})_{i,s} =(\textbf{S}_{{\mathcal U}|_{{\mathcal D}_A}})_{i,s} \Theta_A \ \text{and } \ \Theta_A(I\otimes W_{i,j}(s,t))=(I\otimes U_{i,j}(s,t)|_{{\mathcal D}_A})\Theta_A,
\end{equation*} taking the restriction to the support of ![]() $\Theta_A$, we obtain
$\Theta_A$, we obtain
 \begin{equation*}
\Phi (\textbf{S}_{{\mathcal W}|_{\mathcal L}})_{i,s}=(\textbf{S}_{{\mathcal U}|_{{\mathcal D}_A}})_{i,s}\Phi \ \text{and } \ \Phi(I\otimes W_{i,j}(s,t)|_{\mathcal L})=(I\otimes U_{i,j}(s,t)|_{{\mathcal D}_A})\Phi.
\end{equation*}
\begin{equation*}
\Phi (\textbf{S}_{{\mathcal W}|_{\mathcal L}})_{i,s}=(\textbf{S}_{{\mathcal U}|_{{\mathcal D}_A}})_{i,s}\Phi \ \text{and } \ \Phi(I\otimes W_{i,j}(s,t)|_{\mathcal L})=(I\otimes U_{i,j}(s,t)|_{{\mathcal D}_A})\Phi.
\end{equation*} Consequently, ![]() $\Phi$ is a multi-analytic operator with respect to the multi-shifts
$\Phi$ is a multi-analytic operator with respect to the multi-shifts ![]() $\textbf{S}_{{\mathcal W}|_{\mathcal L}}$ and
$\textbf{S}_{{\mathcal W}|_{\mathcal L}}$ and  $\textbf{S}_{{\mathcal U}|_{{\mathcal D}_A}}$. Due to corollary 5.4 and its proof, we have
$\textbf{S}_{{\mathcal U}|_{{\mathcal D}_A}}$. Due to corollary 5.4 and its proof, we have
 \begin{equation*}
\begin{split}
\mathrm{curv}({A})&= \mathrm{rank}\, \Delta_A(I)- \mathrm{trace\,} [\Delta_{\textbf{S}_{{\mathcal U} |_{{\mathcal D}_A}}}(\Theta_A\Theta_A^*)(N\otimes I_{{\mathcal D}_A})]\\
&= \mathrm{rank}\, \Delta_A(I)- \mathrm{trace\,} [\Delta_{\textbf{S}_{{\mathcal U} |_{{\mathcal D}_A}}}(\Phi\Phi^*)(N\otimes I_{{\mathcal D}_A})]\\
&=\mathrm{rank}\, \Delta_A(I)- \mathrm{trace\,}[(\Phi \Delta_{\textbf{S}_{{\mathcal W}|_{{\mathcal L}}}}(I)\Phi^*)(N\otimes I_{{\mathcal D}_A})]\\
&=\mathrm{rank}\, \Delta_A(I)-\mathrm{trace\,}[\Phi(P_{\mathbb C}\otimes I_{\mathcal L})\Phi^*(N\otimes I_{{\mathcal D}_A})].
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
\mathrm{curv}({A})&= \mathrm{rank}\, \Delta_A(I)- \mathrm{trace\,} [\Delta_{\textbf{S}_{{\mathcal U} |_{{\mathcal D}_A}}}(\Theta_A\Theta_A^*)(N\otimes I_{{\mathcal D}_A})]\\
&= \mathrm{rank}\, \Delta_A(I)- \mathrm{trace\,} [\Delta_{\textbf{S}_{{\mathcal U} |_{{\mathcal D}_A}}}(\Phi\Phi^*)(N\otimes I_{{\mathcal D}_A})]\\
&=\mathrm{rank}\, \Delta_A(I)- \mathrm{trace\,}[(\Phi \Delta_{\textbf{S}_{{\mathcal W}|_{{\mathcal L}}}}(I)\Phi^*)(N\otimes I_{{\mathcal D}_A})]\\
&=\mathrm{rank}\, \Delta_A(I)-\mathrm{trace\,}[\Phi(P_{\mathbb C}\otimes I_{\mathcal L})\Phi^*(N\otimes I_{{\mathcal D}_A})].
\end{split}
\end{equation*} Since ![]() $ \mathrm{curv}({A})=\mathrm{rank}\, \Delta_A(I) \lt \infty$, we must have
$ \mathrm{curv}({A})=\mathrm{rank}\, \Delta_A(I) \lt \infty$, we must have ![]() $\mathrm{trace\,}[\Phi(P_{\mathbb C}\otimes I_{\mathcal L})\Phi^*(N\otimes I_{{\mathcal D}_A})]=0$, which implies
$\mathrm{trace\,}[\Phi(P_{\mathbb C}\otimes I_{\mathcal L})\Phi^*(N\otimes I_{{\mathcal D}_A})]=0$, which implies ![]() $\Phi(P_{\mathbb C}\otimes I_{\mathcal L})\Phi^*(N\otimes I_{{\mathcal D}_A})=0$. Hence, we deduce that
$\Phi(P_{\mathbb C}\otimes I_{\mathcal L})\Phi^*(N\otimes I_{{\mathcal D}_A})=0$. Hence, we deduce that ![]() $\Phi(P_{\mathbb C}\otimes I_{\mathcal L})\Phi^*(P_{(q_1,\ldots, q_k)}\otimes I_{{\mathcal D}_A})=0$ for any
$\Phi(P_{\mathbb C}\otimes I_{\mathcal L})\Phi^*(P_{(q_1,\ldots, q_k)}\otimes I_{{\mathcal D}_A})=0$ for any  $(q_1,\ldots, q_k)\in {\mathbb Z}_+^k$. Therefore,
$(q_1,\ldots, q_k)\in {\mathbb Z}_+^k$. Therefore, ![]() $\Phi(P_{\mathbb C}\otimes I_{\mathcal L})\Phi^*=0$. Taking into account that Ψ is an isometric multi-analytic operator with respect to the multi-shifts
$\Phi(P_{\mathbb C}\otimes I_{\mathcal L})\Phi^*=0$. Taking into account that Ψ is an isometric multi-analytic operator with respect to the multi-shifts ![]() $\textbf{S}_{{\mathcal W}|_{\mathcal L}}$ and
$\textbf{S}_{{\mathcal W}|_{\mathcal L}}$ and  $\textbf{S}_{{\mathcal U}|_{{\mathcal D}_A}}$, we deduce that
$\textbf{S}_{{\mathcal U}|_{{\mathcal D}_A}}$, we deduce that ![]() $\Phi(P_{\mathbb C}\otimes I_{\mathcal L})=0$ and, consequently,
$\Phi(P_{\mathbb C}\otimes I_{\mathcal L})=0$ and, consequently, ![]() $\Phi=0$. On the other hand, using the fact that
$\Phi=0$. On the other hand, using the fact that ![]() $\Phi\Phi^*=\Theta_A\Theta_A^*$ and
$\Phi\Phi^*=\Theta_A\Theta_A^*$ and ![]() $K_A K_A^*+\Theta_A \Theta_A^*=I$, we infer that
$K_A K_A^*+\Theta_A \Theta_A^*=I$, we infer that ![]() $K_A K_A^*=I$. Since A is pure, we have
$K_A K_A^*=I$. Since A is pure, we have ![]() $K_A^* K_A=I$, which shows that KA is a unitary operator. Due to theorem 3.2, we have
$K_A^* K_A=I$, which shows that KA is a unitary operator. Due to theorem 3.2, we have
 \begin{equation*}
A_{i,s}=K_A^*(\textbf{S}_{{\mathcal U}|_{{\mathcal D}_A}})_{i,s} K_A
\end{equation*}
\begin{equation*}
A_{i,s}=K_A^*(\textbf{S}_{{\mathcal U}|_{{\mathcal D}_A}})_{i,s} K_A
\end{equation*} for any ![]() $i\in \{1,\ldots, k\}$ and
$i\in \{1,\ldots, k\}$ and ![]() $s\in \{1,\ldots, n_i\}$. This completes the proof.
$s\in \{1,\ldots, n_i\}$. This completes the proof.
Let ![]() $\textbf{S}_\textbf{z}$ be the standard multi-shift associated with the scalar weights z. Then,
$\textbf{S}_\textbf{z}$ be the standard multi-shift associated with the scalar weights z. Then,
Proof. From the proof of theorem 5.5, we have ![]() $\mathrm{curv}(\textbf{S}_\textbf{z})=\mathrm{rank}\, \Delta_{\textbf{S}_\textbf{z}}(I)=1$. Using corollary 2.8, we complete the proof.
$\mathrm{curv}(\textbf{S}_\textbf{z})=\mathrm{rank}\, \Delta_{\textbf{S}_\textbf{z}}(I)=1$. Using corollary 2.8, we complete the proof.
Let ![]() $\textbf{S}_{\mathcal W}$ be the standard k-tuple of doubly
$\textbf{S}_{\mathcal W}$ be the standard k-tuple of doubly ![]() $I\otimes {\mathcal W}$-commuting pure isometries on the Hilbert space
$I\otimes {\mathcal W}$-commuting pure isometries on the Hilbert space  $ \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal K}$. We say that
$ \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal K}$. We say that  ${\mathcal M}\subset \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal K}$ is a Beurling type [Reference Beurling3] jointly invariant subspace under the operators
${\mathcal M}\subset \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal K}$ is a Beurling type [Reference Beurling3] jointly invariant subspace under the operators ![]() $(\textbf{S}_{\mathcal W})_{i,s}$ and
$(\textbf{S}_{\mathcal W})_{i,s}$ and ![]() $I\otimes W_{i,j}(s,t)$, where
$I\otimes W_{i,j}(s,t)$, where ![]() $i\in\{1,\ldots, k\}$,
$i\in\{1,\ldots, k\}$, ![]() $s\in \{1,\ldots, n_i\}$, and
$s\in \{1,\ldots, n_i\}$, and ![]() $(i,j,s,t)\in \Gamma$, if there are a Hilbert space
$(i,j,s,t)\in \Gamma$, if there are a Hilbert space ![]() ${\mathcal L}$, a standard k-tuple
${\mathcal L}$, a standard k-tuple ![]() $\textbf{S}_{\mathcal U}$ of doubly
$\textbf{S}_{\mathcal U}$ of doubly ![]() $I\otimes {\mathcal U}$-commuting pure isometries on the Hilbert space
$I\otimes {\mathcal U}$-commuting pure isometries on the Hilbert space  $ \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal L}$, and an inner multi-analytic operator
$ \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal L}$, and an inner multi-analytic operator  $\Psi: \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal L}\to
\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal K}$ with respect to the multi-shifts
$\Psi: \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal L}\to
\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal K}$ with respect to the multi-shifts ![]() $\textbf{S}_{\mathcal U}$ and
$\textbf{S}_{\mathcal U}$ and ![]() $\textbf{S}_{\mathcal W}$ such that
$\textbf{S}_{\mathcal W}$ such that
 \begin{equation*}
{\mathcal M}=\Psi \left(\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal L}\right).
\end{equation*}
\begin{equation*}
{\mathcal M}=\Psi \left(\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal L}\right).
\end{equation*} In what follows, we use the notation ![]() $\textbf{S}_{\mathcal W}|_{\mathcal M}$ for the restriction of
$\textbf{S}_{\mathcal W}|_{\mathcal M}$ for the restriction of ![]() $\textbf{S}_{\mathcal W}$ to an invariant subspace
$\textbf{S}_{\mathcal W}$ to an invariant subspace ![]() ${\mathcal M}$ under all the operators
${\mathcal M}$ under all the operators ![]() $(\textbf{S}_{\mathcal W})_{i,s}$ and
$(\textbf{S}_{\mathcal W})_{i,s}$ and ![]() $I\otimes W_{i,j}(s,t)$. In [Reference Popescu28], we proved that the following statements are equivalent:
$I\otimes W_{i,j}(s,t)$. In [Reference Popescu28], we proved that the following statements are equivalent:
(i)
 ${\mathcal M}$ is a Beurling type jointly invariant subspace under the operators
${\mathcal M}$ is a Beurling type jointly invariant subspace under the operators  $(\textbf{S}_{\mathcal W})_{i,s}$ and
$(\textbf{S}_{\mathcal W})_{i,s}$ and  $I\otimes W_{i,j}(s,t)$.
$I\otimes W_{i,j}(s,t)$.(ii)
 $(id-\Phi_{(\textbf{S}_{\mathcal W})_1})\circ\cdots \circ (id-\Phi_{(\textbf{S}_{\mathcal W})_k})(P_{\mathcal M})\geq 0$.
$(id-\Phi_{(\textbf{S}_{\mathcal W})_1})\circ\cdots \circ (id-\Phi_{(\textbf{S}_{\mathcal W})_k})(P_{\mathcal M})\geq 0$.(iii) The k-tuple
 $\textbf{S}_{\mathcal W}|_{\mathcal M}$ is doubly
$\textbf{S}_{\mathcal W}|_{\mathcal M}$ is doubly  $(I\otimes {\mathcal W})|_{\mathcal M}$-commuting.
$(I\otimes {\mathcal W})|_{\mathcal M}$-commuting.(iv) There is an isometric multi-analytic operator
 $\Psi: \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal L}\to
\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal K}$ with respect to the standard multi-shifts
$\Psi: \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal L}\to
\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal K}$ with respect to the standard multi-shifts  $\textbf{S}_{\mathcal U}$ and
$\textbf{S}_{\mathcal U}$ and  $\textbf{S}_{\mathcal W}$ such that
$\textbf{S}_{\mathcal W}$ such that
 \begin{equation*}
{\mathcal M}=\Psi \left(\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal L}\right).
\end{equation*}
\begin{equation*}
{\mathcal M}=\Psi \left(\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal L}\right).
\end{equation*}
If ![]() ${\mathcal M}$ is a Beurling type jointly invariant subspace under
${\mathcal M}$ is a Beurling type jointly invariant subspace under ![]() $\textbf{S}_{\mathcal W}$ and
$\textbf{S}_{\mathcal W}$ and ![]() $I\otimes {\mathcal W}$, we say that it has a finite rank if
$I\otimes {\mathcal W}$, we say that it has a finite rank if ![]() $\textbf{S}_{\mathcal W}|_{\mathcal M}$ has a finite rank defect operator.
$\textbf{S}_{\mathcal W}|_{\mathcal M}$ has a finite rank defect operator.
Definition 5.7. Let ![]() $\textbf{S}_{\mathcal W}$ be the standard k-tuple of doubly
$\textbf{S}_{\mathcal W}$ be the standard k-tuple of doubly ![]() $I\otimes {\mathcal W}$-commuting row isometries on the Hilbert space
$I\otimes {\mathcal W}$-commuting row isometries on the Hilbert space  $ \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal K}$, and let
$ \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal K}$, and let ![]() ${\mathcal M}$ and
${\mathcal M}$ and ![]() ${\mathcal N}$ be invariant subspaces under
${\mathcal N}$ be invariant subspaces under ![]() $\textbf{S}_{\mathcal W}$ and
$\textbf{S}_{\mathcal W}$ and ![]() $I\otimes {\mathcal W}$. We say that
$I\otimes {\mathcal W}$. We say that ![]() $ {\mathcal M}$ and
$ {\mathcal M}$ and ![]() ${\mathcal N}$ are unitarily equivalent if there is a unitary operator
${\mathcal N}$ are unitarily equivalent if there is a unitary operator ![]() $\Gamma:{\mathcal M}\to {\mathcal N}$ such that
$\Gamma:{\mathcal M}\to {\mathcal N}$ such that
Proposition 5.8. Let ![]() ${\mathcal M}$ and
${\mathcal M}$ and ![]() ${\mathcal N}$ be finite rank Beurling type jointly invariant subspace under
${\mathcal N}$ be finite rank Beurling type jointly invariant subspace under ![]() $\textbf{S}_{\mathcal W}$ and
$\textbf{S}_{\mathcal W}$ and ![]() $I\otimes {\mathcal W}$. If
$I\otimes {\mathcal W}$. If ![]() ${\mathcal M}$ and
${\mathcal M}$ and ![]() ${\mathcal N}$ are unitarily equivalent, then
${\mathcal N}$ are unitarily equivalent, then
 \begin{equation*}
\mathrm{curv} (\textbf{S}_{\mathcal W}|_{\mathcal M})= \mathrm{rank}\, \Delta_{\textbf{S}_{\mathcal W}|_{\mathcal M}}(I_{\mathcal M})= \mathrm{curv} (\textbf{S}_{\mathcal W}|_{\mathcal N})=\mathrm{rank}\, \Delta_{\textbf{S}_{\mathcal W}|_{\mathcal N}}(I_{\mathcal N}).
\end{equation*}
\begin{equation*}
\mathrm{curv} (\textbf{S}_{\mathcal W}|_{\mathcal M})= \mathrm{rank}\, \Delta_{\textbf{S}_{\mathcal W}|_{\mathcal M}}(I_{\mathcal M})= \mathrm{curv} (\textbf{S}_{\mathcal W}|_{\mathcal N})=\mathrm{rank}\, \Delta_{\textbf{S}_{\mathcal W}|_{\mathcal N}}(I_{\mathcal N}).
\end{equation*}Proof. Due to the remarks preceding definition 5.7, ![]() $\textbf{S}_{\mathcal W}|_{\mathcal M}$ is a doubly
$\textbf{S}_{\mathcal W}|_{\mathcal M}$ is a doubly ![]() $(I\otimes {\mathcal W})|_{\mathcal M}$-commuting k-tuple of pure row isometry and there is an isometric multi-analytic operator
$(I\otimes {\mathcal W})|_{\mathcal M}$-commuting k-tuple of pure row isometry and there is an isometric multi-analytic operator  $\Psi: \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal L}\to
\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal K}$ with respect to the standard multi-shifts
$\Psi: \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal L}\to
\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal K}$ with respect to the standard multi-shifts ![]() $\textbf{S}_{\mathcal U}$ and
$\textbf{S}_{\mathcal U}$ and ![]() $\textbf{S}_{\mathcal W}$ such that
$\textbf{S}_{\mathcal W}$ such that
 \begin{equation*}
{\mathcal M}=\Psi \left(\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal L}\right).
\end{equation*}
\begin{equation*}
{\mathcal M}=\Psi \left(\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal L}\right).
\end{equation*} Consequently, ![]() $P_{\mathcal M}=\Psi\Psi^*$ and
$P_{\mathcal M}=\Psi\Psi^*$ and
 \begin{equation*}
\Delta_{\textbf{S}_{\mathcal W}|_{\mathcal M}}(I_{\mathcal M})=\Delta_{\textbf{S}_{\mathcal W}|_{\mathcal M}}(P_{\mathcal M})=\Psi \Delta_{\textbf{S}_{\mathcal U}}(I)\Psi^*|_{\mathcal M}=\Psi(P_{\mathbb C}\otimes I_{\mathcal L})\Psi^*|_{\mathcal M}.
\end{equation*}
\begin{equation*}
\Delta_{\textbf{S}_{\mathcal W}|_{\mathcal M}}(I_{\mathcal M})=\Delta_{\textbf{S}_{\mathcal W}|_{\mathcal M}}(P_{\mathcal M})=\Psi \Delta_{\textbf{S}_{\mathcal U}}(I)\Psi^*|_{\mathcal M}=\Psi(P_{\mathbb C}\otimes I_{\mathcal L})\Psi^*|_{\mathcal M}.
\end{equation*} Using the latter relation and taking into account that Ψ is an isometry, we can prove that  $\mathrm{rank}\, \Delta_{\textbf{S}_{\mathcal W}|_{\mathcal M}}(I_{\mathcal M})=\dim {\mathcal L}$. Indeed, if
$\mathrm{rank}\, \Delta_{\textbf{S}_{\mathcal W}|_{\mathcal M}}(I_{\mathcal M})=\dim {\mathcal L}$. Indeed, if ![]() $\{w_\sigma\}_{\sigma\in\Sigma}$ is an orthonormal basis for the subspace
$\{w_\sigma\}_{\sigma\in\Sigma}$ is an orthonormal basis for the subspace ![]() ${\mathcal L}$, then
${\mathcal L}$, then
 \begin{equation*}\{\Psi(\chi_{(\alpha_1,\ldots, \alpha_k)}\otimes w_\sigma):\ \sigma\in \Sigma, (\alpha_1,\ldots, \alpha_k)\in {\mathbb F}_{n_1}^+\times \cdots\times {\mathbb F}_{n_k}^+\}
\end{equation*}
\begin{equation*}\{\Psi(\chi_{(\alpha_1,\ldots, \alpha_k)}\otimes w_\sigma):\ \sigma\in \Sigma, (\alpha_1,\ldots, \alpha_k)\in {\mathbb F}_{n_1}^+\times \cdots\times {\mathbb F}_{n_k}^+\}
\end{equation*} is an orthonormal basis for ![]() ${\mathcal M}$. Moreover,
${\mathcal M}$. Moreover, ![]() $\overline{\Psi(P_{\mathbb C}\otimes I_{\mathcal L})\Psi^*|_{\mathcal M}}$ is equal to the closure of the range of the defect operator
$\overline{\Psi(P_{\mathbb C}\otimes I_{\mathcal L})\Psi^*|_{\mathcal M}}$ is equal to the closure of the range of the defect operator  $\Delta_{\textbf{S}_{\mathcal W}|_{\mathcal M}}(I_{\mathcal M})$ and also coincides with the closed linear span of the vectors
$\Delta_{\textbf{S}_{\mathcal W}|_{\mathcal M}}(I_{\mathcal M})$ and also coincides with the closed linear span of the vectors ![]() $\{\Psi(1\otimes w_\sigma):\ \sigma\in \Sigma\}$. Therefore,
$\{\Psi(1\otimes w_\sigma):\ \sigma\in \Sigma\}$. Therefore,
 \begin{equation*}\mathrm{rank}\, \Delta_{\textbf{S}_{\mathcal W}|_{\mathcal M}}(I_{\mathcal M})=\mathrm{card}\, \Sigma= \dim {\mathcal L}.
\end{equation*}
\begin{equation*}\mathrm{rank}\, \Delta_{\textbf{S}_{\mathcal W}|_{\mathcal M}}(I_{\mathcal M})=\mathrm{card}\, \Sigma= \dim {\mathcal L}.
\end{equation*} Now, we prove that ![]() $\mathrm{curv} (\textbf{S}_{\mathcal W}|_{\mathcal M})=\dim {\mathcal L}$. As in the proof of theorem 3.3, using the definition of the
$\mathrm{curv} (\textbf{S}_{\mathcal W}|_{\mathcal M})=\dim {\mathcal L}$. As in the proof of theorem 3.3, using the definition of the ![]() $I\otimes {\mathcal W}$-twisted multi-shift
$I\otimes {\mathcal W}$-twisted multi-shift ![]() $\textbf{S}:=\textbf{S}_{\mathcal U}$ acting on
$\textbf{S}:=\textbf{S}_{\mathcal U}$ acting on  $\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal L}$, one can show that
$\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal L}$, one can show that
 \begin{equation*}
\begin{split}
\Phi^{q_i+1}_{\textbf{S}_i}(I)\left( \chi_{(\alpha_1,\ldots, \alpha_k)}\otimes h\right)
=\begin{cases}
\chi_{(\alpha_1,\ldots, \alpha_k)}\otimes h,&\quad \text{if } |\alpha_i|\geq q_i+1\\
0, &\quad \text{otherwise }
\end{cases}
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
\Phi^{q_i+1}_{\textbf{S}_i}(I)\left( \chi_{(\alpha_1,\ldots, \alpha_k)}\otimes h\right)
=\begin{cases}
\chi_{(\alpha_1,\ldots, \alpha_k)}\otimes h,&\quad \text{if } |\alpha_i|\geq q_i+1\\
0, &\quad \text{otherwise }
\end{cases}
\end{split}
\end{equation*} for any ![]() $q_i\in {\mathbb N}$. Using this relation, it is easy to see that
$q_i\in {\mathbb N}$. Using this relation, it is easy to see that  $
(id-\Phi^{q_1+1}_{\textbf{S}_1})\circ\cdots \circ (id-\Phi^{q_k+1}_{\textbf{S}_k})(I)
$ is the orthogonal projection of
$
(id-\Phi^{q_1+1}_{\textbf{S}_1})\circ\cdots \circ (id-\Phi^{q_k+1}_{\textbf{S}_k})(I)
$ is the orthogonal projection of  $\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal L}$ onto
$\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal L}$ onto
Due to corollary 3.4, we have
 \begin{equation*}
\mathrm{curv} (\textbf{S}_{\mathcal U})=\lim_{q_1\to\infty}\cdots\lim_{q_k\to\infty}
\frac{\mathrm{trace\,}\left[(id-\Phi_{\textbf{S}_1}^{q_1+1})\circ \cdots \circ (id-\Phi_{\textbf{S}_k}^{q_k+1})(I)\right]}
{\prod_{i=1}^k(1+n_i+\cdots + n_i^{q_i})}=\dim {\mathcal L}.
\end{equation*}
\begin{equation*}
\mathrm{curv} (\textbf{S}_{\mathcal U})=\lim_{q_1\to\infty}\cdots\lim_{q_k\to\infty}
\frac{\mathrm{trace\,}\left[(id-\Phi_{\textbf{S}_1}^{q_1+1})\circ \cdots \circ (id-\Phi_{\textbf{S}_k}^{q_k+1})(I)\right]}
{\prod_{i=1}^k(1+n_i+\cdots + n_i^{q_i})}=\dim {\mathcal L}.
\end{equation*}Now, note that
 \begin{equation*}
\begin{aligned}
&(id-\Phi_{(\textbf{S}_{\mathcal W})_1|_{\mathcal M}}^{q_1+1})\circ \cdots \circ (id-\Phi_{(\textbf{S}_{\mathcal W})_k|_{\mathcal M}}^{q_k+1})(I_{\mathcal M})= \Psi (id-\Phi_{(\textbf{S}_{\mathcal U})_1}^{q_1+1})\circ \cdots \circ \\ & \qquad\qquad\qquad\qquad\qquad(id-\Phi_{(\textbf{S}_{\mathcal U})_k|}^{q_k+1})(I) \Psi^*|{\mathcal M}.
\end{aligned}
\end{equation*}
\begin{equation*}
\begin{aligned}
&(id-\Phi_{(\textbf{S}_{\mathcal W})_1|_{\mathcal M}}^{q_1+1})\circ \cdots \circ (id-\Phi_{(\textbf{S}_{\mathcal W})_k|_{\mathcal M}}^{q_k+1})(I_{\mathcal M})= \Psi (id-\Phi_{(\textbf{S}_{\mathcal U})_1}^{q_1+1})\circ \cdots \circ \\ & \qquad\qquad\qquad\qquad\qquad(id-\Phi_{(\textbf{S}_{\mathcal U})_k|}^{q_k+1})(I) \Psi^*|{\mathcal M}.
\end{aligned}
\end{equation*}Using again corollary 3.4, as above, we deduce that
Consequently, we have  $\mathrm{curv} (\textbf{S}_{\mathcal W}|_{\mathcal M})=\mathrm{rank}\, \Delta_{\textbf{S}_{\mathcal W}|_{\mathcal M}}(I_{\mathcal M})$. Similarly, we have that
$\mathrm{curv} (\textbf{S}_{\mathcal W}|_{\mathcal M})=\mathrm{rank}\, \Delta_{\textbf{S}_{\mathcal W}|_{\mathcal M}}(I_{\mathcal M})$. Similarly, we have that ![]() $\textbf{S}_{\mathcal W}|_{\mathcal N}$ is a doubly
$\textbf{S}_{\mathcal W}|_{\mathcal N}$ is a doubly ![]() $(I\otimes {\mathcal W})|_{\mathcal N}$-commuting k-tuple and
$(I\otimes {\mathcal W})|_{\mathcal N}$-commuting k-tuple and  $\mathrm{curv} (\textbf{S}_{\mathcal W}|_{\mathcal N})=\mathrm{rank}\, \Delta_{\textbf{S}_{\mathcal W}|_{\mathcal N}}(I_{\mathcal N})$. Now, since the curvature is invariant up to unitary equivalence, if
$\mathrm{curv} (\textbf{S}_{\mathcal W}|_{\mathcal N})=\mathrm{rank}\, \Delta_{\textbf{S}_{\mathcal W}|_{\mathcal N}}(I_{\mathcal N})$. Now, since the curvature is invariant up to unitary equivalence, if ![]() ${\mathcal M}$ and
${\mathcal M}$ and ![]() ${\mathcal N}$ are unitarily equivalent, then
${\mathcal N}$ are unitarily equivalent, then ![]() $
\mathrm{curv} (\textbf{S}_{\mathcal W}|_{\mathcal M})= \mathrm{curv} (\textbf{S}_{\mathcal W}|_{\mathcal N}).
$ The proof is complete.
$
\mathrm{curv} (\textbf{S}_{\mathcal W}|_{\mathcal M})= \mathrm{curv} (\textbf{S}_{\mathcal W}|_{\mathcal N}).
$ The proof is complete.
6. Invariant subspaces under  ${\mathcal U}$-twisted multi-shifts and their multiplicity
${\mathcal U}$-twisted multi-shifts and their multiplicity
In this section, we introduce the notion of multiplicity for the invariant subspaces under the multi-shifts with a finite rank defect operator, prove the existence, provide several asymptotic formulas, and connect it to the curvature invariant. Under appropriate conditions, we show that there is a trace class multiplicity operator whose trace coincides with the multiplicity. We also obtain results concerning the semi-continuity for the curvature and the multiplicity invariants. Finally, we provide necessary and sufficient conditions when ![]() $A|_{\mathcal M}$ is in
$A|_{\mathcal M}$ is in  $\textbf{B}^{{\mathcal U}|_{\mathcal M}}({\mathcal H})$ and consider some consequences.
$\textbf{B}^{{\mathcal U}|_{\mathcal M}}({\mathcal H})$ and consider some consequences.
In what follows, S is the standard k-tuple of doubly ![]() $I\otimes {\mathcal U}$-commuting row isometries on the Hilbert space
$I\otimes {\mathcal U}$-commuting row isometries on the Hilbert space  $ \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal H}$ and assume that
$ \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal H}$ and assume that ![]() $\dim {\mathcal H} \lt \infty$. If
$\dim {\mathcal H} \lt \infty$. If ![]() ${\mathcal M}$ is any invariant subspace under S and
${\mathcal M}$ is any invariant subspace under S and ![]() $I\otimes {\mathcal U}$, we introduce the multiplicity of
$I\otimes {\mathcal U}$, we introduce the multiplicity of ![]() ${\mathcal M}$ by setting
${\mathcal M}$ by setting
 \begin{equation*}
m({\mathcal M}):=
\lim_{m\to\infty}\frac{1}{\left(\begin{matrix} m+k\\ k\end{matrix}\right)}\sum_{{q_1\geq 0,\ldots, q_k\geq 0}\atop {q_1+\cdots +q_k\leq m}} \frac{
\mathrm{trace\,}\left[ P_{\mathcal M} (P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal H}) \right]}
{\mathrm{trace\,}\left[P_{(q_1,\ldots, q_k)}\right]}.
\end{equation*}
\begin{equation*}
m({\mathcal M}):=
\lim_{m\to\infty}\frac{1}{\left(\begin{matrix} m+k\\ k\end{matrix}\right)}\sum_{{q_1\geq 0,\ldots, q_k\geq 0}\atop {q_1+\cdots +q_k\leq m}} \frac{
\mathrm{trace\,}\left[ P_{\mathcal M} (P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal H}) \right]}
{\mathrm{trace\,}\left[P_{(q_1,\ldots, q_k)}\right]}.
\end{equation*}Theorem 6.1 Let S be the standard k-tuple of doubly ![]() $I\otimes {\mathcal U}$-commuting row isometries on the Hilbert space
$I\otimes {\mathcal U}$-commuting row isometries on the Hilbert space  $ \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal H}$, where
$ \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal H}$, where ![]() $\dim {\mathcal H} \lt \infty$. If
$\dim {\mathcal H} \lt \infty$. If ![]() ${\mathcal M}$ is any invariant subspace under S and
${\mathcal M}$ is any invariant subspace under S and ![]() $I\otimes {\mathcal U}$, the multiplicity of
$I\otimes {\mathcal U}$, the multiplicity of ![]() ${\mathcal M}$ exists and
${\mathcal M}$ exists and
 \begin{equation*}
\begin{split}
m({\mathcal M})&=\lim_{m\to\infty}\frac{1}{\left(\begin{matrix} m+k-1\\ k-1\end{matrix}\right)}\sum_{{q_1\geq 0,\ldots, q_k\geq 0}\atop {q_1+\cdots +q_k= m}}\frac{
\mathrm{trace\,}\left[ P_{\mathcal M} (P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal H})\right]}{\mathrm{trace\,}[P_{(q_1,\ldots, q_k)}]}\\
&=\lim_{q_1\to\infty}\cdots\lim_{q_k\to\infty}\frac{
\mathrm{trace\,}\left[ P_{\mathcal M} (P_{\leq (q_1,\ldots, q_k)}\otimes I_{\mathcal H})\right]}{\mathrm{trace\,}[P_{\leq (q_1,\ldots, q_k)}]}\\
&=\lim_{(q_1,\ldots, q_k)\in {\mathbb Z}_+^k} \frac{
\mathrm{trace\,}\left[ P_{\mathcal M} (P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal H})\right]}{\mathrm{trace\,}[P_{(q_1,\ldots, q_k)}]}.
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
m({\mathcal M})&=\lim_{m\to\infty}\frac{1}{\left(\begin{matrix} m+k-1\\ k-1\end{matrix}\right)}\sum_{{q_1\geq 0,\ldots, q_k\geq 0}\atop {q_1+\cdots +q_k= m}}\frac{
\mathrm{trace\,}\left[ P_{\mathcal M} (P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal H})\right]}{\mathrm{trace\,}[P_{(q_1,\ldots, q_k)}]}\\
&=\lim_{q_1\to\infty}\cdots\lim_{q_k\to\infty}\frac{
\mathrm{trace\,}\left[ P_{\mathcal M} (P_{\leq (q_1,\ldots, q_k)}\otimes I_{\mathcal H})\right]}{\mathrm{trace\,}[P_{\leq (q_1,\ldots, q_k)}]}\\
&=\lim_{(q_1,\ldots, q_k)\in {\mathbb Z}_+^k} \frac{
\mathrm{trace\,}\left[ P_{\mathcal M} (P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal H})\right]}{\mathrm{trace\,}[P_{(q_1,\ldots, q_k)}]}.
\end{split}
\end{equation*}Proof. Set ![]() $T:=(T_1,\ldots, T_n)$ with
$T:=(T_1,\ldots, T_n)$ with ![]() $T_i:=(T_{i,1},\ldots, T_{i,n_i})$ with
$T_i:=(T_{i,1},\ldots, T_{i,n_i})$ with ![]() $T_{i,s}:=P_{{\mathcal M}^\perp} \textbf{S}_{i,s}|_{{\mathcal M}^\perp}$ for any
$T_{i,s}:=P_{{\mathcal M}^\perp} \textbf{S}_{i,s}|_{{\mathcal M}^\perp}$ for any ![]() $i\in \{1,\ldots, k\}$ and
$i\in \{1,\ldots, k\}$ and ![]() $s\in \{1,\ldots, n_i\}$. In this case, we also use the notation
$s\in \{1,\ldots, n_i\}$. In this case, we also use the notation ![]() $T=P_{{\mathcal M}^\perp} \textbf{S}|_{{\mathcal M}^\perp}$. Since
$T=P_{{\mathcal M}^\perp} \textbf{S}|_{{\mathcal M}^\perp}$. Since ![]() $T_{i,s}^*=\textbf{S}_{i,s}^*|_{{\mathcal M}^\perp}$ and each
$T_{i,s}^*=\textbf{S}_{i,s}^*|_{{\mathcal M}^\perp}$ and each ![]() $\textbf{S}_i:=[\textbf{S}_{i,1}\cdots \textbf{S}_{i,n_i}]$ is a row contraction, Ti is also a row contraction. On the other hand, since
$\textbf{S}_i:=[\textbf{S}_{i,1}\cdots \textbf{S}_{i,n_i}]$ is a row contraction, Ti is also a row contraction. On the other hand, since
 \begin{equation*}
\sum_{\alpha\in {\mathbb F}_{n_i}^+, |\alpha|=q} T_{i,\alpha}T_{i,\alpha}^*=P_{{\mathcal M}^\perp} \left(\sum_{\alpha\in {\mathbb F}_{n_i}^+, |\alpha|=q} \textbf{S}_{i,\alpha}\textbf{S}_{i,\alpha}^*\right)|_{{\mathcal M}^\perp}
\end{equation*}
\begin{equation*}
\sum_{\alpha\in {\mathbb F}_{n_i}^+, |\alpha|=q} T_{i,\alpha}T_{i,\alpha}^*=P_{{\mathcal M}^\perp} \left(\sum_{\alpha\in {\mathbb F}_{n_i}^+, |\alpha|=q} \textbf{S}_{i,\alpha}\textbf{S}_{i,\alpha}^*\right)|_{{\mathcal M}^\perp}
\end{equation*} and ![]() $[\textbf{S}_{i,1}\cdots \textbf{S}_{i,n_i}]$ is a pure row isometry, we deduce that Ti is a pure row contraction. Also note that
$[\textbf{S}_{i,1}\cdots \textbf{S}_{i,n_i}]$ is a pure row isometry, we deduce that Ti is a pure row contraction. Also note that
On the other hand, since ![]() ${\mathcal M}$ is reducing under each
${\mathcal M}$ is reducing under each ![]() $I\otimes U_{i,j}(s,t)$, we have
$I\otimes U_{i,j}(s,t)$, we have
 \begin{equation*}
\begin{split}
T_{j,t}^*T_{i,s}^*&=\textbf{S}_{j,t}^*\textbf{S}_{i,s}^* |_{{\mathcal M}^\perp}=\textbf{S}_{i,s}^*\textbf{S}_{j,t}^*(I\otimes U_{i,j}(s,t)^*)|_{{\mathcal M}^\perp}\\
&=T_{i,s}^* T_{j,t}^* W_{i,j}(s,t)^*
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
T_{j,t}^*T_{i,s}^*&=\textbf{S}_{j,t}^*\textbf{S}_{i,s}^* |_{{\mathcal M}^\perp}=\textbf{S}_{i,s}^*\textbf{S}_{j,t}^*(I\otimes U_{i,j}(s,t)^*)|_{{\mathcal M}^\perp}\\
&=T_{i,s}^* T_{j,t}^* W_{i,j}(s,t)^*
\end{split}
\end{equation*} where ![]() $W_{i,j}(s,t):=(I\otimes U_{i,j}(s,t))|_{{\mathcal M}^\perp}$. Hence,
$W_{i,j}(s,t):=(I\otimes U_{i,j}(s,t))|_{{\mathcal M}^\perp}$. Hence, ![]() $T_{i,s}T_{j,t}=W_{ij}(s,t) T_{j,t}T_{i,s}$ for any
$T_{i,s}T_{j,t}=W_{ij}(s,t) T_{j,t}T_{i,s}$ for any ![]() $(i,j,s,t)\in \Gamma$. Also note that, since
$(i,j,s,t)\in \Gamma$. Also note that, since
for any ![]() $p\in \{1,\ldots, k\}$,
$p\in \{1,\ldots, k\}$, ![]() $q\in \{1,\ldots, n_p\}$, and
$q\in \{1,\ldots, n_p\}$, and ![]() $(i,j,s,t)\in \Gamma$, we have that
$(i,j,s,t)\in \Gamma$, we have that ![]() $W_{i,j}(s,t)^* T_{p,q}^*=T_{p,q}^*W_{i,j}(s,t)^*$. Hence,
$W_{i,j}(s,t)^* T_{p,q}^*=T_{p,q}^*W_{i,j}(s,t)^*$. Hence, ![]() $T_{p,q} W_{i,j}(s,t)=W_{i,j}(s,t) T_{p,q}$. Therefore,
$T_{p,q} W_{i,j}(s,t)=W_{i,j}(s,t) T_{p,q}$. Therefore,  $T\in \textbf{B}_{reg}^{\mathcal W}({\mathcal H})$. Taking into account that
$T\in \textbf{B}_{reg}^{\mathcal W}({\mathcal H})$. Taking into account that ![]() $\Delta_T(I_{{\mathcal M}^\perp})=
P_{{\mathcal M}^\perp} \Delta_\textbf{S}(I)|_{{\mathcal M}^\perp}$, we deduce that
$\Delta_T(I_{{\mathcal M}^\perp})=
P_{{\mathcal M}^\perp} \Delta_\textbf{S}(I)|_{{\mathcal M}^\perp}$, we deduce that
Now, we need to show that  $\Phi_{\textbf{S}_1}^{q_1}\circ \cdots \circ \Phi_{\textbf{S}_k}^{q_k}({\Delta_\textbf{S}}(I))=P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal H}$. Indeed, as we saw in the proof of theorem 3.3,
$\Phi_{\textbf{S}_1}^{q_1}\circ \cdots \circ \Phi_{\textbf{S}_k}^{q_k}({\Delta_\textbf{S}}(I))=P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal H}$. Indeed, as we saw in the proof of theorem 3.3,
 \begin{equation*}
\begin{split}
(\Phi_{\textbf{S}_1}^{q_1}- \Phi_{\textbf{S}_1}^{q_1+1})\circ \cdots \circ (\Phi_{\textbf{S}_k}^{q_k}- \Phi_{\textbf{S}_k}^{q_k+1})(I)
=P_{(q_1,\ldots, q_k)} \otimes I_{\mathcal H}.
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
(\Phi_{\textbf{S}_1}^{q_1}- \Phi_{\textbf{S}_1}^{q_1+1})\circ \cdots \circ (\Phi_{\textbf{S}_k}^{q_k}- \Phi_{\textbf{S}_k}^{q_k+1})(I)
=P_{(q_1,\ldots, q_k)} \otimes I_{\mathcal H}.
\end{split}
\end{equation*}Since, due to proposition 2.3,
 \begin{equation*}\Phi_{\textbf{S}_1}^{q_1}\circ \cdots \circ \Phi_{\textbf{S}_k}^{q_k}({\Delta_\textbf{S}}(I))
=
(\Phi_{\textbf{S}_1}^{q_1}- \Phi_{\textbf{S}_1}^{q_1+1})\circ \cdots \circ (\Phi_{\textbf{S}_k}^{q_k}- \Phi_{\textbf{S}_k}^{q_k+1})(I),
\end{equation*}
\begin{equation*}\Phi_{\textbf{S}_1}^{q_1}\circ \cdots \circ \Phi_{\textbf{S}_k}^{q_k}({\Delta_\textbf{S}}(I))
=
(\Phi_{\textbf{S}_1}^{q_1}- \Phi_{\textbf{S}_1}^{q_1+1})\circ \cdots \circ (\Phi_{\textbf{S}_k}^{q_k}- \Phi_{\textbf{S}_k}^{q_k+1})(I),
\end{equation*} our assertion follows. Now, using again that ![]() ${\mathcal M}$ is an invariant subspace under S, we have
${\mathcal M}$ is an invariant subspace under S, we have
 \begin{equation*}
\begin{split}
\mathrm{trace\,}\left[ \Phi_{T_1}^{q_1}\circ \cdots \circ \Phi_{T_k}^{q_k}({\Delta_{T}}(I_{{\mathcal M}^\perp}))\right]
&=\mathrm{trace\,}\left[ P_{{\mathcal M}^\perp}\Phi_{\textbf{S}_1}^{q_1}\circ \cdots \circ \Phi_{\textbf{S}_k}^{q_k}({\Delta_\textbf{S}}(I))|_{{\mathcal M}^\perp}\right]\\
&=\mathrm{trace\,}\left[ P_{{\mathcal M}^\perp} (P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal H}) \right].
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
\mathrm{trace\,}\left[ \Phi_{T_1}^{q_1}\circ \cdots \circ \Phi_{T_k}^{q_k}({\Delta_{T}}(I_{{\mathcal M}^\perp}))\right]
&=\mathrm{trace\,}\left[ P_{{\mathcal M}^\perp}\Phi_{\textbf{S}_1}^{q_1}\circ \cdots \circ \Phi_{\textbf{S}_k}^{q_k}({\Delta_\textbf{S}}(I))|_{{\mathcal M}^\perp}\right]\\
&=\mathrm{trace\,}\left[ P_{{\mathcal M}^\perp} (P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal H}) \right].
\end{split}
\end{equation*}Hence, and due to theorem 3.3 and corollary 3.4,
 \begin{equation*}
\begin{split}
\mathrm{curv}(T)&=
\lim_{(q_1,\ldots, q_k)\in {\mathbb Z}_+^k} \frac{\mathrm{trace\,}\left[ \Phi_{T_1}^{q_1}\circ \cdots \circ \Phi_{T_k}^{q_k}({\Delta_{T}}(I_{{\mathcal M}^\perp}))\right]}{n_1^{q_1}\cdots n_k^{q_k}}\\
&=
\lim_{(q_1,\ldots, q_k)\in {\mathbb Z}_+^k} \frac{\mathrm{trace\,}\left[ P_{{\mathcal M}^\perp} (P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal H}) \right]}{n_1^{q_1}\cdots n_k^{q_k}}
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
\mathrm{curv}(T)&=
\lim_{(q_1,\ldots, q_k)\in {\mathbb Z}_+^k} \frac{\mathrm{trace\,}\left[ \Phi_{T_1}^{q_1}\circ \cdots \circ \Phi_{T_k}^{q_k}({\Delta_{T}}(I_{{\mathcal M}^\perp}))\right]}{n_1^{q_1}\cdots n_k^{q_k}}\\
&=
\lim_{(q_1,\ldots, q_k)\in {\mathbb Z}_+^k} \frac{\mathrm{trace\,}\left[ P_{{\mathcal M}^\perp} (P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal H}) \right]}{n_1^{q_1}\cdots n_k^{q_k}}
\end{split}
\end{equation*}exists. This implies
 \begin{equation*}
\begin{split}
&\lim_{(q_1,\ldots, q_k)\in {\mathbb Z}_+^k} \frac{
\mathrm{trace\,}\left[ P_{\mathcal M} (P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal H})\right]}{\mathrm{trace\,}[P_{(q_1,\ldots, q_k)}]}\\
&=
\lim_{(q_1,\ldots, q_k)\in {\mathbb Z}_+^k} \frac{
\mathrm{trace\,}\left[ (P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal H})\right]}{\mathrm{trace\,}[P_{(q_1,\ldots, q_k)}]} -\lim_{(q_1,\ldots, q_k)\in {\mathbb Z}_+^k} \frac{
\mathrm{trace\,}\left[ P_{{\mathcal M}^\perp} (P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal H})\right]}{\mathrm{trace\,}[P_{(q_1,\ldots, q_k)}]}\\
&=\dim {\mathcal H}- \lim_{(q_1,\ldots, q_k)\in {\mathbb Z}_+^k} \frac{
\mathrm{trace\,}\left[ P_{{\mathcal M}^\perp} (P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal H})\right]}{\mathrm{trace\,}[P_{(q_1,\ldots, q_k)}]}=\dim {\mathcal H}- \mathrm{curv}(T).
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
&\lim_{(q_1,\ldots, q_k)\in {\mathbb Z}_+^k} \frac{
\mathrm{trace\,}\left[ P_{\mathcal M} (P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal H})\right]}{\mathrm{trace\,}[P_{(q_1,\ldots, q_k)}]}\\
&=
\lim_{(q_1,\ldots, q_k)\in {\mathbb Z}_+^k} \frac{
\mathrm{trace\,}\left[ (P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal H})\right]}{\mathrm{trace\,}[P_{(q_1,\ldots, q_k)}]} -\lim_{(q_1,\ldots, q_k)\in {\mathbb Z}_+^k} \frac{
\mathrm{trace\,}\left[ P_{{\mathcal M}^\perp} (P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal H})\right]}{\mathrm{trace\,}[P_{(q_1,\ldots, q_k)}]}\\
&=\dim {\mathcal H}- \lim_{(q_1,\ldots, q_k)\in {\mathbb Z}_+^k} \frac{
\mathrm{trace\,}\left[ P_{{\mathcal M}^\perp} (P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal H})\right]}{\mathrm{trace\,}[P_{(q_1,\ldots, q_k)}]}=\dim {\mathcal H}- \mathrm{curv}(T).
\end{split}
\end{equation*}Now, using again theorem 3.3 and corollary 3.4, one can easily complete the proof.
The multiplicity invariant measures the size of the invariant subspaces under S and ![]() $I\otimes {\mathcal U}$ in the Hilbert space
$I\otimes {\mathcal U}$ in the Hilbert space  $\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal H}$. Note that
$\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal H}$. Note that  $m( \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal H})=\dim{\mathcal H}$, and if
$m( \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal H})=\dim{\mathcal H}$, and if ![]() ${\mathcal M}_1$ and
${\mathcal M}_1$ and ![]() ${\mathcal M}_2$ are orthogonal invariant subspaces, then
${\mathcal M}_2$ are orthogonal invariant subspaces, then ![]() $m({\mathcal M}_1\oplus {\mathcal M}_2)=m({\mathcal M}_1)+m({\mathcal M}_2)$.
$m({\mathcal M}_1\oplus {\mathcal M}_2)=m({\mathcal M}_1)+m({\mathcal M}_2)$.
Corollary 6.2. Under the hypothesis of theorem 6.1, the following statements hold:
(i)
 $
m({\mathcal M})= \dim {\mathcal H}- \mathrm{curv}(P_{{\mathcal M}^\perp} \textbf{S}_{\mathcal U}|_{{\mathcal M}^\perp})
$
$
m({\mathcal M})= \dim {\mathcal H}- \mathrm{curv}(P_{{\mathcal M}^\perp} \textbf{S}_{\mathcal U}|_{{\mathcal M}^\perp})
$(ii) If
 ${\mathcal M}_1,\ldots, {\mathcal M}_n$ are orthogonal invariant subspaces under S and
${\mathcal M}_1,\ldots, {\mathcal M}_n$ are orthogonal invariant subspaces under S and  $I\otimes {\mathcal U}$, then
$I\otimes {\mathcal U}$, then
 \begin{align*}
&\mathrm{curv}(P_{({\mathcal M}_1\oplus\cdots\oplus {\mathcal M}_n)^\perp} \textbf{S}_{\mathcal U}|_{({\mathcal M}_1\oplus\cdots\oplus {\mathcal M}_n)^\perp})
\\ & \qquad=\sum_{i=1}^n \mathrm{curv}(P_{{\mathcal M}_i^\perp} \textbf{S}_{\mathcal U}|_{{\mathcal M}_i^\perp})-(n-1)\dim {\mathcal H}.
\end{align*}
\begin{align*}
&\mathrm{curv}(P_{({\mathcal M}_1\oplus\cdots\oplus {\mathcal M}_n)^\perp} \textbf{S}_{\mathcal U}|_{({\mathcal M}_1\oplus\cdots\oplus {\mathcal M}_n)^\perp})
\\ & \qquad=\sum_{i=1}^n \mathrm{curv}(P_{{\mathcal M}_i^\perp} \textbf{S}_{\mathcal U}|_{{\mathcal M}_i^\perp})-(n-1)\dim {\mathcal H}.
\end{align*}(iii) If
 $T:=P_{{\mathcal M}^\perp} \textbf{S}_{\mathcal U}|_{{\mathcal M}^\perp}$ and KT is the noncommutative Berezin kernel associated with T, then
$T:=P_{{\mathcal M}^\perp} \textbf{S}_{\mathcal U}|_{{\mathcal M}^\perp}$ and KT is the noncommutative Berezin kernel associated with T, then
 \begin{equation*}
m({\mathcal M})=\lim_{(q_1,\ldots, q_k)\in {\mathbb Z}_+^k} \mathrm{trace\,}\left[ \Delta_{\textbf{S}_{\mathcal U}}(I-K_T K_T^*) (N_{\leq (q_1,\ldots, q_k)}\otimes I_{\mathcal H})\right].
\end{equation*}
\begin{equation*}
m({\mathcal M})=\lim_{(q_1,\ldots, q_k)\in {\mathbb Z}_+^k} \mathrm{trace\,}\left[ \Delta_{\textbf{S}_{\mathcal U}}(I-K_T K_T^*) (N_{\leq (q_1,\ldots, q_k)}\otimes I_{\mathcal H})\right].
\end{equation*}
Proof. The first relation follows from the proof of theorem 6.1. Item (ii) follows from item (i) and the fact that ![]() $m({\mathcal M}_1\oplus\cdots\oplus {\mathcal M}_n)=\sum_{i=1}^n m({\mathcal M}_i)$. To prove item (iii), we use theorem 5.2 which shows that
$m({\mathcal M}_1\oplus\cdots\oplus {\mathcal M}_n)=\sum_{i=1}^n m({\mathcal M}_i)$. To prove item (iii), we use theorem 5.2 which shows that
 \begin{equation*}
\mathrm{curv}({T})=\lim_{(q_1,\ldots, q_k)\in {\mathbb Z}_+^k} \mathrm{trace\,}\left[ \Delta_{\textbf{S}_{\mathcal U}}(K_T K_T^*) (N_{\leq (q_1,\ldots, q_k)}\otimes I_{\mathcal H})\right].
\end{equation*}
\begin{equation*}
\mathrm{curv}({T})=\lim_{(q_1,\ldots, q_k)\in {\mathbb Z}_+^k} \mathrm{trace\,}\left[ \Delta_{\textbf{S}_{\mathcal U}}(K_T K_T^*) (N_{\leq (q_1,\ldots, q_k)}\otimes I_{\mathcal H})\right].
\end{equation*}Now, using item (i), we complete the proof.
Corollary 6.3. Let ![]() $\textbf{S}_\textbf{z}$ be the standard z-twisted multi-shift on
$\textbf{S}_\textbf{z}$ be the standard z-twisted multi-shift on  $\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)$. If
$\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)$. If ![]() ${\mathcal M}$ is an invariant subspace under
${\mathcal M}$ is an invariant subspace under ![]() $\textbf{S}_\textbf{z}\otimes I_{\mathcal E}$ with
$\textbf{S}_\textbf{z}\otimes I_{\mathcal E}$ with ![]() $\dim{\mathcal E} \lt \infty$, then its multiplicity exists. In particular, if
$\dim{\mathcal E} \lt \infty$, then its multiplicity exists. In particular, if ![]() $n_1=\cdots=n_k=1$, then
$n_1=\cdots=n_k=1$, then ![]() ${\mathcal M}$ is in the vector-valued Hardy space
${\mathcal M}$ is in the vector-valued Hardy space ![]() $H^2({\mathbb D}^k)\otimes {\mathcal E}$ and
$H^2({\mathbb D}^k)\otimes {\mathcal E}$ and
 \begin{equation*}
m({\mathcal M})=\lim_{m\to\infty}\frac{\mathrm{trace\,}[P_{\mathcal M} (P_{\leq m}\otimes I_{\mathcal E})]}{\mathrm{trace\,}[P_{\leq m}]},
\end{equation*}
\begin{equation*}
m({\mathcal M})=\lim_{m\to\infty}\frac{\mathrm{trace\,}[P_{\mathcal M} (P_{\leq m}\otimes I_{\mathcal E})]}{\mathrm{trace\,}[P_{\leq m}]},
\end{equation*} where ![]() $P_{\leq m}$ is the orthogonal projection on the polynomials of degree
$P_{\leq m}$ is the orthogonal projection on the polynomials of degree ![]() $\leq m$.
$\leq m$.
We remark that if ![]() $n_1=\cdots=n_k=1$, the result of corollary 6.3 is a twisted version of Fang’s [Reference Fang9] commutative result for
$n_1=\cdots=n_k=1$, the result of corollary 6.3 is a twisted version of Fang’s [Reference Fang9] commutative result for ![]() $H^2({\mathbb D}^k)\otimes {\mathcal E}$ when
$H^2({\mathbb D}^k)\otimes {\mathcal E}$ when ![]() $\textbf{z}=\{1\}$.
$\textbf{z}=\{1\}$.
The next result shows that the multiplicity invariant is lower semi-continuous.
Theorem 6.4 Let ![]() $\textbf{S}_{{\mathcal U}}$ be the
$\textbf{S}_{{\mathcal U}}$ be the ![]() ${\mathcal U}$-twisted multi-shift with
${\mathcal U}$-twisted multi-shift with ![]() ${\mathcal U}\subset B({\mathcal H})$ and
${\mathcal U}\subset B({\mathcal H})$ and ![]() $\dim {\mathcal H} \lt \infty$, acting on the Hilbert space
$\dim {\mathcal H} \lt \infty$, acting on the Hilbert space  $\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal H}$. If
$\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal H}$. If ![]() ${\mathcal M}$ and
${\mathcal M}$ and ![]() ${\mathcal M}_p$ are invariant subspaces of
${\mathcal M}_p$ are invariant subspaces of ![]() $\textbf{S}_{{\mathcal U}}$ and
$\textbf{S}_{{\mathcal U}}$ and ![]() $I\otimes{\mathcal U}$ such that
$I\otimes{\mathcal U}$ such that ![]() $ P_{{\mathcal M}_p}\to P_{\mathcal M}$ in the weak operator topology, then
$ P_{{\mathcal M}_p}\to P_{\mathcal M}$ in the weak operator topology, then
 \begin{equation*}
\liminf_{p\to\infty}m({\mathcal M}_p)\geq m({\mathcal M})
\end{equation*}
\begin{equation*}
\liminf_{p\to\infty}m({\mathcal M}_p)\geq m({\mathcal M})
\end{equation*}and
 \begin{equation*}
\limsup_{p\to\infty}\mathrm{curv} (P_{{\mathcal M}_p^\perp} \textbf{S}_{\mathcal U}|_{{\mathcal M}_p^\perp})\leq
\mathrm{curv} (P_{{\mathcal M}^\perp} \textbf{S}_{\mathcal U}|_{{\mathcal M}^\perp}).
\end{equation*}
\begin{equation*}
\limsup_{p\to\infty}\mathrm{curv} (P_{{\mathcal M}_p^\perp} \textbf{S}_{\mathcal U}|_{{\mathcal M}_p^\perp})\leq
\mathrm{curv} (P_{{\mathcal M}^\perp} \textbf{S}_{\mathcal U}|_{{\mathcal M}^\perp}).
\end{equation*}Proof. Let ![]() $B:=(B_1,\ldots, B_k)$ with
$B:=(B_1,\ldots, B_k)$ with ![]() $B_i:=(B_{i,1},\ldots, B_{i,n_i})$ and
$B_i:=(B_{i,1},\ldots, B_{i,n_i})$ and ![]() $B_{i,s}:=P_{{\mathcal M}^\perp}(\textbf{S}_{\mathcal U})_{i,s} |_{{\mathcal M}^\perp}$. In a similar manner, we define
$B_{i,s}:=P_{{\mathcal M}^\perp}(\textbf{S}_{\mathcal U})_{i,s} |_{{\mathcal M}^\perp}$. In a similar manner, we define  $B^{(p)}:=(B_1^{(p)},\ldots, B_k^{(p)})$. As in the proof of theorem 6.1, we have
$B^{(p)}:=(B_1^{(p)},\ldots, B_k^{(p)})$. As in the proof of theorem 6.1, we have
 \begin{equation*}
\begin{split}
\mathrm{trace\,}[\Phi_{B_1}^{q_1}\circ \cdots \circ \Phi_{B_k}^{q_k} ({\Delta_{B}}(I_{{\mathcal M}^\perp}))]
&=\mathrm{trace\,}[P_{{\mathcal M}^\perp}(P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal H})]\\
&=n_1^{q_1}\cdots n_k^{q_k}\dim{\mathcal H}- \mathrm{trace\,}[P_{{\mathcal M}}(P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal H})]
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
\mathrm{trace\,}[\Phi_{B_1}^{q_1}\circ \cdots \circ \Phi_{B_k}^{q_k} ({\Delta_{B}}(I_{{\mathcal M}^\perp}))]
&=\mathrm{trace\,}[P_{{\mathcal M}^\perp}(P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal H})]\\
&=n_1^{q_1}\cdots n_k^{q_k}\dim{\mathcal H}- \mathrm{trace\,}[P_{{\mathcal M}}(P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal H})]
\end{split}
\end{equation*} and a similar relation associated with ![]() $B^{(p)}$ holds. Since
$B^{(p)}$ holds. Since ![]() $ P_{{\mathcal M}_p}\to P_{\mathcal M}$ in the weak operator topology, we have
$ P_{{\mathcal M}_p}\to P_{\mathcal M}$ in the weak operator topology, we have
 \begin{equation*}
\lim_{p\to\infty} \mathrm{trace\,}[P_{{\mathcal M}_m}(P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal H})]=\mathrm{trace\,}[P_{{\mathcal M}}(P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal H})].
\end{equation*}
\begin{equation*}
\lim_{p\to\infty} \mathrm{trace\,}[P_{{\mathcal M}_m}(P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal H})]=\mathrm{trace\,}[P_{{\mathcal M}}(P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal H})].
\end{equation*}Consequently, we obtain
 \begin{equation*}
\lim_{p\to\infty}\mathrm{trace\,}[\Phi_{B_1^{(p)}}^{q_1}\circ \cdots \circ \Phi_{B_k^{(p)}}^{q_k} ({\Delta_{B^{(p)}}}(I_{{\mathcal M}_p^\perp}))]=\mathrm{trace\,}[\Phi_{B_1}^{q_1}\circ \cdots \circ \Phi_{B_k}^{q_k} ({\Delta_{B}}(I_{{\mathcal M}^\perp}))].
\end{equation*}
\begin{equation*}
\lim_{p\to\infty}\mathrm{trace\,}[\Phi_{B_1^{(p)}}^{q_1}\circ \cdots \circ \Phi_{B_k^{(p)}}^{q_k} ({\Delta_{B^{(p)}}}(I_{{\mathcal M}_p^\perp}))]=\mathrm{trace\,}[\Phi_{B_1}^{q_1}\circ \cdots \circ \Phi_{B_k}^{q_k} ({\Delta_{B}}(I_{{\mathcal M}^\perp}))].
\end{equation*} As in the proof of theorem 3.6, one can show that  $\limsup_{p\to\infty}\mathrm{curv}({B}^{(m)})\leq \mathrm{curv}({B} )$. On the other hand, using corollary 6.2, we have
$\limsup_{p\to\infty}\mathrm{curv}({B}^{(m)})\leq \mathrm{curv}({B} )$. On the other hand, using corollary 6.2, we have
 \begin{equation*}
m({\mathcal M})=\dim{\mathcal H}- \mathrm{curv}(B) \quad \text{and } \quad
m({\mathcal M}_p)=\dim{\mathcal H}- \mathrm{curv}(B^{(p)}).
\end{equation*}
\begin{equation*}
m({\mathcal M})=\dim{\mathcal H}- \mathrm{curv}(B) \quad \text{and } \quad
m({\mathcal M}_p)=\dim{\mathcal H}- \mathrm{curv}(B^{(p)}).
\end{equation*} Consequently, we obtain ![]() $\liminf_{p\to\infty}m({\mathcal M}_p)\geq m({\mathcal M})$. The proof is complete.
$\liminf_{p\to\infty}m({\mathcal M}_p)\geq m({\mathcal M})$. The proof is complete.
Since the proof of the next result is straightforward, we should omit it.
Proposition 6.5. Let ![]() $A=(A_1,\ldots, A_k)\in B({\mathcal H})^{n_1+\cdots + n_k}$ be a
$A=(A_1,\ldots, A_k)\in B({\mathcal H})^{n_1+\cdots + n_k}$ be a ![]() ${\mathcal U}$-commuting tuple, and let
${\mathcal U}$-commuting tuple, and let ![]() ${\mathcal M}\subset {\mathcal H}$ be an invariant subspace under A and
${\mathcal M}\subset {\mathcal H}$ be an invariant subspace under A and ![]() ${\mathcal U}$. If
${\mathcal U}$. If ![]() $B:=P_{{\mathcal M}^\perp} A|_{{\mathcal M}^\perp}$, then the following statements hold:
$B:=P_{{\mathcal M}^\perp} A|_{{\mathcal M}^\perp}$, then the following statements hold:
(i) B is
 ${\mathcal U}|_{{\mathcal M}^\perp}$-commuting.
${\mathcal U}|_{{\mathcal M}^\perp}$-commuting.(ii)
 $\Delta_{rB} (I_{{\mathcal M}^\perp})=P_{{\mathcal M}^\perp}\Delta_{rA}(I_{\mathcal H})|_{{\mathcal M}^\perp}$ for any
$\Delta_{rB} (I_{{\mathcal M}^\perp})=P_{{\mathcal M}^\perp}\Delta_{rA}(I_{\mathcal H})|_{{\mathcal M}^\perp}$ for any  $r\in [0,1]$.
$r\in [0,1]$.(iii) If
 $A\in \textbf{B}^{{\mathcal U}}({\mathcal H})$, then
$A\in \textbf{B}^{{\mathcal U}}({\mathcal H})$, then  $B\in \textbf{B}^{{\mathcal U}|_{{\mathcal M}^\perp}}({{\mathcal M}^\perp})$.
$B\in \textbf{B}^{{\mathcal U}|_{{\mathcal M}^\perp}}({{\mathcal M}^\perp})$.(iv) If
 $A\in \textbf{B}^{{\mathcal U}}_{reg}({\mathcal H})$, then
$A\in \textbf{B}^{{\mathcal U}}_{reg}({\mathcal H})$, then  $B\in \textbf{B}_{reg}^{{\mathcal U}|_{{\mathcal M}^\perp}}({{\mathcal M}^\perp})$.
$B\in \textbf{B}_{reg}^{{\mathcal U}|_{{\mathcal M}^\perp}}({{\mathcal M}^\perp})$.
Theorem 6.6 Let ![]() $A:=(A_1,\ldots, A_k)$ be an element in the
$A:=(A_1,\ldots, A_k)$ be an element in the ![]() ${\mathcal U}$-twisted polyball
${\mathcal U}$-twisted polyball  $ \textbf{B}^{\mathcal U}({\mathcal H})$ such that
$ \textbf{B}^{\mathcal U}({\mathcal H})$ such that ![]() $\Delta_A(I)$ is a positive trace class operator. If
$\Delta_A(I)$ is a positive trace class operator. If ![]() ${\mathcal M}$ is an invariant subspace under A and
${\mathcal M}$ is an invariant subspace under A and ![]() ${\mathcal U}$ with
${\mathcal U}$ with ![]() $\dim {\mathcal M} \lt \infty$, then
$\dim {\mathcal M} \lt \infty$, then  $P_{{\mathcal M}^\perp}{A}|_{{\mathcal M}^\perp}\in \textbf{B}^{{\mathcal U}|_{{\mathcal M}^\perp}}({\mathcal M}^\perp)$ has a positive trace class defect operator and
$P_{{\mathcal M}^\perp}{A}|_{{\mathcal M}^\perp}\in \textbf{B}^{{\mathcal U}|_{{\mathcal M}^\perp}}({\mathcal M}^\perp)$ has a positive trace class defect operator and
Proof. Set ![]() $B:=(B_1,\ldots, B_k)$ and
$B:=(B_1,\ldots, B_k)$ and ![]() $B_i:=(B_{i,1},\ldots, B_{i,n_i})$, where
$B_i:=(B_{i,1},\ldots, B_{i,n_i})$, where ![]() $B_{i,s}:=P_{{\mathcal M}^\perp} A_{i,s}|_{{\mathcal M}^\perp}$ for
$B_{i,s}:=P_{{\mathcal M}^\perp} A_{i,s}|_{{\mathcal M}^\perp}$ for ![]() $i\in \{1,\ldots, k\}$ and
$i\in \{1,\ldots, k\}$ and ![]() $s\in \{1,\ldots, n_i\}$. Note that
$s\in \{1,\ldots, n_i\}$. Note that  $\Phi_{B_i}^{q_i}(I_{{\mathcal M}^\perp})=P_{{\mathcal M}^\perp} \Phi_{A_i}^{q_i}(I_{\mathcal H})|_{{\mathcal M}^\perp}$ and
$\Phi_{B_i}^{q_i}(I_{{\mathcal M}^\perp})=P_{{\mathcal M}^\perp} \Phi_{A_i}^{q_i}(I_{\mathcal H})|_{{\mathcal M}^\perp}$ and ![]() $\Delta_B(I_{{\mathcal M}^\perp})=P_{{\mathcal M}^\perp}\Delta_A(I_{\mathcal H})|_{{\mathcal M}^\perp}\geq 0$. Consequently,
$\Delta_B(I_{{\mathcal M}^\perp})=P_{{\mathcal M}^\perp}\Delta_A(I_{\mathcal H})|_{{\mathcal M}^\perp}\geq 0$. Consequently, ![]() $\mathrm{trace}\,\Delta_B(I_{{\mathcal M}^\perp})\leq
\mathrm{trace}\, \Delta_A(I_{\mathcal H}) \lt \infty$. It is easy to see that, taking into account that
$\mathrm{trace}\,\Delta_B(I_{{\mathcal M}^\perp})\leq
\mathrm{trace}\, \Delta_A(I_{\mathcal H}) \lt \infty$. It is easy to see that, taking into account that
 \begin{equation*}
\|\left(id -\Phi_{A_1}^{q_1+1}\right)\circ \cdots \circ\left(id -\Phi_{A_k}^{q_k+1}\right)(I_{\mathcal H})\|\leq 2^k,
\end{equation*}
\begin{equation*}
\|\left(id -\Phi_{A_1}^{q_1+1}\right)\circ \cdots \circ\left(id -\Phi_{A_k}^{q_k+1}\right)(I_{\mathcal H})\|\leq 2^k,
\end{equation*}we obtain
 \begin{equation*}
\begin{aligned}
&\mathrm{trace}\left[\left(id -\Phi_{A_1}^{q_1+1}\right)\circ \cdots \circ\left(id -\Phi_{A_k}^{q_k+1}\right)(I_{\mathcal H})\right]\\
&= \mathrm{trace}\left[P_{{\mathcal M}^\perp}\left(id -\Phi_{A_1}^{q_1+1}\right)\circ \cdots \circ\left(id -\Phi_{A_k}^{q_k+1}\right)(I_{\mathcal H})|_{{\mathcal M}^\perp}\right]\\ & \qquad+\mathrm{trace}\left[P_{{\mathcal M}}\left(id -\Phi_{A_1}^{q_1+1}\right)\circ \cdots \circ\left(id -\Phi_{A_k}^{q_k+1}\right)(I_{\mathcal H})\right]\\
&\leq \mathrm{trace}\left[\left(id -\Phi_{B_1}^{q_1+1}\right)\circ \cdots \circ\left(id -\Phi_{B_k}^{q_k+1}\right)(I_{{\mathcal M}^\perp})\right] + 2^k \dim {\mathcal M}.
\end{aligned}
\end{equation*}
\begin{equation*}
\begin{aligned}
&\mathrm{trace}\left[\left(id -\Phi_{A_1}^{q_1+1}\right)\circ \cdots \circ\left(id -\Phi_{A_k}^{q_k+1}\right)(I_{\mathcal H})\right]\\
&= \mathrm{trace}\left[P_{{\mathcal M}^\perp}\left(id -\Phi_{A_1}^{q_1+1}\right)\circ \cdots \circ\left(id -\Phi_{A_k}^{q_k+1}\right)(I_{\mathcal H})|_{{\mathcal M}^\perp}\right]\\ & \qquad+\mathrm{trace}\left[P_{{\mathcal M}}\left(id -\Phi_{A_1}^{q_1+1}\right)\circ \cdots \circ\left(id -\Phi_{A_k}^{q_k+1}\right)(I_{\mathcal H})\right]\\
&\leq \mathrm{trace}\left[\left(id -\Phi_{B_1}^{q_1+1}\right)\circ \cdots \circ\left(id -\Phi_{B_k}^{q_k+1}\right)(I_{{\mathcal M}^\perp})\right] + 2^k \dim {\mathcal M}.
\end{aligned}
\end{equation*}Hence, we deduce that
 \begin{equation*}
\begin{split}
&\left|\frac{\mathrm{trace}\left[\left(id -\Phi_{A_1}^{q_1+1}\right)\circ \cdots \circ\left(id -\Phi_{A_k}^{q_k+1}\right)(I_{\mathcal H})\right]}{{\prod_{i=1}^k(1+n_i+\cdots + n_i^{q_i})}}\right.\\ & \qquad\qquad \left. -\frac{\mathrm{trace}\left[\left(id -\Phi_{B_1}^{q_1+1}\right)\circ \cdots \circ\left(id -\Phi_{B_k}^{q_k+1}\right)(I_{{\mathcal M}^\perp})\right]}{{\prod_{i=1}^k(1+n_i+\cdots + n_i^{q_i})}}
\right|\\
&\qquad\qquad\leq \frac{2^k \dim{\mathcal M}}{{\prod_{i=1}^k(1+n_i+\cdots + n_i^{q_i})}}.
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
&\left|\frac{\mathrm{trace}\left[\left(id -\Phi_{A_1}^{q_1+1}\right)\circ \cdots \circ\left(id -\Phi_{A_k}^{q_k+1}\right)(I_{\mathcal H})\right]}{{\prod_{i=1}^k(1+n_i+\cdots + n_i^{q_i})}}\right.\\ & \qquad\qquad \left. -\frac{\mathrm{trace}\left[\left(id -\Phi_{B_1}^{q_1+1}\right)\circ \cdots \circ\left(id -\Phi_{B_k}^{q_k+1}\right)(I_{{\mathcal M}^\perp})\right]}{{\prod_{i=1}^k(1+n_i+\cdots + n_i^{q_i})}}
\right|\\
&\qquad\qquad\leq \frac{2^k \dim{\mathcal M}}{{\prod_{i=1}^k(1+n_i+\cdots + n_i^{q_i})}}.
\end{split}
\end{equation*} Using corollary 3.4, we deduce that ![]() $\mathrm{curv}({A})=\mathrm{curv}(B)$. The proof is complete.
$\mathrm{curv}({A})=\mathrm{curv}(B)$. The proof is complete.
According to [Reference Popescu27], the reducing subspaces under the standard ![]() ${\mathcal U}$-twisted multi-shift
${\mathcal U}$-twisted multi-shift ![]() $\textbf{S}_{\mathcal U}$ on the Hilbert space
$\textbf{S}_{\mathcal U}$ on the Hilbert space  $\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal H}$ are of the form
$\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal H}$ are of the form  ${\mathcal M}=\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal L}$, where
${\mathcal M}=\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal L}$, where ![]() ${\mathcal L}\subset {\mathcal H}$ is a reducing subspace under all the unitaries
${\mathcal L}\subset {\mathcal H}$ is a reducing subspace under all the unitaries ![]() $U_{i,j}(s,t)$ in
$U_{i,j}(s,t)$ in ![]() ${\mathcal U}$.
${\mathcal U}$.
Using some results from [Reference Popescu28], we prove the following.
Proposition 6.7. Let ![]() $\textbf{S}_{\mathcal U}$ be the
$\textbf{S}_{\mathcal U}$ be the ![]() ${\mathcal U}$-twisted multi-shift on
${\mathcal U}$-twisted multi-shift on  $\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal H}$, and let
$\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal H}$, and let ![]() ${\mathcal M}\ $ be an invariant subspace under
${\mathcal M}\ $ be an invariant subspace under ![]() $\textbf{S}_{\mathcal U}$ and
$\textbf{S}_{\mathcal U}$ and ![]() ${\mathcal U}$ which does not contain nontrivial reducing subspaces for
${\mathcal U}$ which does not contain nontrivial reducing subspaces for ![]() $\textbf{S}_{\mathcal U}$. Then, the compression
$\textbf{S}_{\mathcal U}$. Then, the compression ![]() $T:=P_{{\mathcal M}^\perp} \textbf{S}_{{\mathcal U}}|_{{\mathcal M}^\perp}$ has a characteristic function if and only if
$T:=P_{{\mathcal M}^\perp} \textbf{S}_{{\mathcal U}}|_{{\mathcal M}^\perp}$ has a characteristic function if and only if ![]() ${\mathcal M}$ is a Beurling type invariant subspace.
${\mathcal M}$ is a Beurling type invariant subspace.
Proof. Under the given hypothesis, ![]() ${\mathcal M}^\perp$ is a cyclic subspace for
${\mathcal M}^\perp$ is a cyclic subspace for ![]() $\textbf{S}_{{\mathcal U}}$. Therefore,
$\textbf{S}_{{\mathcal U}}$. Therefore, ![]() $\textbf{S}_{{\mathcal U}}$ is a minimal isometric dilation of
$\textbf{S}_{{\mathcal U}}$ is a minimal isometric dilation of ![]() $T:=P_{{\mathcal M}^\perp} \textbf{S}_{{\mathcal U}}|_{{\mathcal M}^\perp}$. On the other hand, according to [Reference Popescu28] (see theorem 3.3 and its proof) if
$T:=P_{{\mathcal M}^\perp} \textbf{S}_{{\mathcal U}}|_{{\mathcal M}^\perp}$. On the other hand, according to [Reference Popescu28] (see theorem 3.3 and its proof) if
 \begin{equation*}{K_{T}}: {\mathcal M}^\perp \to \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+) \otimes {\mathcal D}_T,\qquad {\mathcal D}_T:=\overline{{\Delta_{T}}(I)({\mathcal M}^\perp)},\end{equation*}
\begin{equation*}{K_{T}}: {\mathcal M}^\perp \to \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+) \otimes {\mathcal D}_T,\qquad {\mathcal D}_T:=\overline{{\Delta_{T}}(I)({\mathcal M}^\perp)},\end{equation*} is the noncommutative Berezin kernel associated with T, then the subspace ![]() $K_T {\mathcal M}^\perp$ is co-invariant under each operator
$K_T {\mathcal M}^\perp$ is co-invariant under each operator ![]() $(\textbf{S}_{{\mathcal U}})_{i,s} $ for any
$(\textbf{S}_{{\mathcal U}})_{i,s} $ for any ![]() $i\in \{1,\ldots, k\}$,
$i\in \{1,\ldots, k\}$, ![]() $ j\in \{1,\ldots, n_i\}$ and the dilation provided by the relation
$ j\in \{1,\ldots, n_i\}$ and the dilation provided by the relation
 \begin{equation*}T_{i,s}= {K_{T}^*}(\textbf{S}_{{\mathcal U}|_{{\mathcal D}_T}})_{i,s}) {K_{T}}
\end{equation*}
\begin{equation*}T_{i,s}= {K_{T}^*}(\textbf{S}_{{\mathcal U}|_{{\mathcal D}_T}})_{i,s}) {K_{T}}
\end{equation*} is minimal. Due to the uniqueness of the minimal isometric dilation of pure elements in ![]() ${\mathcal U}$-twisted polyballs (see theorem 3.3 from [Reference Popescu28]), there is a unitary operator
${\mathcal U}$-twisted polyballs (see theorem 3.3 from [Reference Popescu28]), there is a unitary operator
 \begin{equation*}
\Psi:\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal D}_T \to \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal H}
\end{equation*}
\begin{equation*}
\Psi:\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal D}_T \to \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal H}
\end{equation*} such that  $
\Psi(\textbf{S}_{{\mathcal U}|_{{\mathcal D}_T}})_{i,s} =(\textbf{S}_{{\mathcal U}})_{i,s}) \Psi
$ and
$
\Psi(\textbf{S}_{{\mathcal U}|_{{\mathcal D}_T}})_{i,s} =(\textbf{S}_{{\mathcal U}})_{i,s}) \Psi
$ and ![]() $\Psi K_T=V$, where V is the injection of the subspace
$\Psi K_T=V$, where V is the injection of the subspace ![]() ${\mathcal M}^\perp$ into
${\mathcal M}^\perp$ into  $\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal H}$. Since Ψ is a unitary operator, we also deduce that
$\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal H}$. Since Ψ is a unitary operator, we also deduce that  $
\Psi(\textbf{S}_{{\mathcal U}|_{{\mathcal D}_T}})^*_{i,s}) =(\textbf{S}_{{\mathcal U}})^*_{i,s} \Psi.
$ Consequently,
$
\Psi(\textbf{S}_{{\mathcal U}|_{{\mathcal D}_T}})^*_{i,s}) =(\textbf{S}_{{\mathcal U}})^*_{i,s} \Psi.
$ Consequently,
 \begin{equation*}
\begin{split}
\Psi (P_{\mathbb C}\otimes I_{{\mathcal D}_T})=\Psi \Delta_{\textbf{S}_{{\mathcal U}|_{{\mathcal D}_T}}}(I_{{\mathcal D}_T})
=\Delta_{\textbf{S}_{{\mathcal U}}}(I_{{\mathcal H}})\Psi=(P_{\mathbb C}\otimes I_{\mathcal H})\Psi.
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
\Psi (P_{\mathbb C}\otimes I_{{\mathcal D}_T})=\Psi \Delta_{\textbf{S}_{{\mathcal U}|_{{\mathcal D}_T}}}(I_{{\mathcal D}_T})
=\Delta_{\textbf{S}_{{\mathcal U}}}(I_{{\mathcal H}})\Psi=(P_{\mathbb C}\otimes I_{\mathcal H})\Psi.
\end{split}
\end{equation*} Hence, we deduce that ![]() $\Psi{\mathcal D}_T={\mathcal H}$. Setting
$\Psi{\mathcal D}_T={\mathcal H}$. Setting ![]() $\psi:=\Psi|_{{\mathcal D}_T}:{\mathcal D}_T\to {\mathcal H}$ and taking into account that Ψ is multi-analytic, we deduce that
$\psi:=\Psi|_{{\mathcal D}_T}:{\mathcal D}_T\to {\mathcal H}$ and taking into account that Ψ is multi-analytic, we deduce that ![]() $\Psi=I\otimes \psi$. Therefore,
$\Psi=I\otimes \psi$. Therefore, ![]() $\psi:{\mathcal D}_T\to {\mathcal H}$ is a unitary operator such that
$\psi:{\mathcal D}_T\to {\mathcal H}$ is a unitary operator such that ![]() $(I\otimes \psi){K_T}=V$. Consequently,
$(I\otimes \psi){K_T}=V$. Consequently, ![]() ${K_{T}} {K_{T}^*}=(I\otimes \psi^*)P_{{\mathcal M}^\perp} (I\otimes \psi)$ and
${K_{T}} {K_{T}^*}=(I\otimes \psi^*)P_{{\mathcal M}^\perp} (I\otimes \psi)$ and
Due to the remarks preceding definition 5.7, ![]() ${\mathcal M}$ is a Beurling type invariant subspace if and only if
${\mathcal M}$ is a Beurling type invariant subspace if and only if ![]() $\Delta_{\textbf{S}_{{\mathcal U}}}(P_{\mathcal M})\geq 0$. Using the above identity, we deduce that
$\Delta_{\textbf{S}_{{\mathcal U}}}(P_{\mathcal M})\geq 0$. Using the above identity, we deduce that ![]() ${\Delta_{\textbf{S}_{{\mathcal U}}}}(I-{K_{T}}{K_{T}^*})\geq 0$. Due to theorem 6.1 from [Reference Popescu28], the later inequality is equivalent to T having a characteristic function. The proof is complete.
${\Delta_{\textbf{S}_{{\mathcal U}}}}(I-{K_{T}}{K_{T}^*})\geq 0$. Due to theorem 6.1 from [Reference Popescu28], the later inequality is equivalent to T having a characteristic function. The proof is complete.
Theorem 6.8 Let S be the standard k-tuple of doubly ![]() $I\otimes {\mathcal U}$-commuting row isometries on the Hilbert space
$I\otimes {\mathcal U}$-commuting row isometries on the Hilbert space  $ \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal H}$, where
$ \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal H}$, where ![]() $\dim {\mathcal H} \lt \infty$. If
$\dim {\mathcal H} \lt \infty$. If ![]() ${\mathcal M}$ is a Beurling type invariant subspace under S and
${\mathcal M}$ is a Beurling type invariant subspace under S and ![]() $I\otimes {\mathcal U}$ which does not contain nontrivial reducing subspace under S, then the multiplicity operator
$I\otimes {\mathcal U}$ which does not contain nontrivial reducing subspace under S, then the multiplicity operator ![]() $\Delta_\textbf{S}(P_{\mathcal M})(N\otimes I)$ is trace class and
$\Delta_\textbf{S}(P_{\mathcal M})(N\otimes I)$ is trace class and
In particular, this relation holds for Beurling type invariant subspace under ![]() $\textbf{S}_\textbf{z}\otimes I_{\mathcal E}$ with
$\textbf{S}_\textbf{z}\otimes I_{\mathcal E}$ with ![]() $\dim{\mathcal E} \lt \infty$.
$\dim{\mathcal E} \lt \infty$.
Proof. According to proposition 6.7 and its proof, we have
where ![]() $\psi:{\mathcal D}_T\to {\mathcal H}$ is a unitary operator. On the other hand, due to corollary 5.4 and its proof, we have
$\psi:{\mathcal D}_T\to {\mathcal H}$ is a unitary operator. On the other hand, due to corollary 5.4 and its proof, we have
Consequently, using corollary 6.2, we deduce that
 \begin{equation*}
\begin{split}
m({\mathcal M})&= \dim {\mathcal H}- \mathrm{curv}(T)\\
&=\mathrm{trace\,} [\Delta_{\textbf{S}_{\mathcal U}}(I-K_TK_T^*)(N\otimes I_{{\mathcal D}_T})]\\
&=\mathrm{trace\,} [(I\otimes \psi^*)\Delta_{\textbf{S}_{{\mathcal U}}}(P_{\mathcal M}) (I\otimes \psi)(N\otimes I_{{\mathcal D}_T}) \\
&=\mathrm{trace\,}\left[ \Delta_\textbf{S}(P_{\mathcal M})(N\otimes I)\right].
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
m({\mathcal M})&= \dim {\mathcal H}- \mathrm{curv}(T)\\
&=\mathrm{trace\,} [\Delta_{\textbf{S}_{\mathcal U}}(I-K_TK_T^*)(N\otimes I_{{\mathcal D}_T})]\\
&=\mathrm{trace\,} [(I\otimes \psi^*)\Delta_{\textbf{S}_{{\mathcal U}}}(P_{\mathcal M}) (I\otimes \psi)(N\otimes I_{{\mathcal D}_T}) \\
&=\mathrm{trace\,}\left[ \Delta_\textbf{S}(P_{\mathcal M})(N\otimes I)\right].
\end{split}
\end{equation*}The proof is complete.
We remark that if ![]() $A=(A_1,\ldots, A_k)$ with
$A=(A_1,\ldots, A_k)$ with ![]() $A_i=(A_{i,1},\ldots, A_{i,n_i})$ is an element in
$A_i=(A_{i,1},\ldots, A_{i,n_i})$ is an element in  $\textbf{B}_{reg}^{{\mathcal U}}({\mathcal H})$ and
$\textbf{B}_{reg}^{{\mathcal U}}({\mathcal H})$ and ![]() ${\mathcal M}$ is an invariant subspace under A and
${\mathcal M}$ is an invariant subspace under A and ![]() ${\mathcal U}$, then
${\mathcal U}$, then ![]() $A|_{\mathcal M}$ is not necessarily in the regular
$A|_{\mathcal M}$ is not necessarily in the regular ![]() ${\mathcal U}|_{\mathcal M}$-twisted polyball, where
${\mathcal U}|_{\mathcal M}$-twisted polyball, where ![]() $A|_{\mathcal M}$ is defined by taking the restrictions
$A|_{\mathcal M}$ is defined by taking the restrictions ![]() $A_{i,s}|{\mathcal M}$. However, we have the following result.
$A_{i,s}|{\mathcal M}$. However, we have the following result.
Proposition 6.9. Let ![]() $A=(A_1,\ldots, A_k)\in B({\mathcal H})^{n_1+\cdots + n_k}$ be a
$A=(A_1,\ldots, A_k)\in B({\mathcal H})^{n_1+\cdots + n_k}$ be a ![]() ${\mathcal U}$-commuting tuple, and let
${\mathcal U}$-commuting tuple, and let ![]() ${\mathcal M}\subset {\mathcal H}$ be an invariant subspace under A and
${\mathcal M}\subset {\mathcal H}$ be an invariant subspace under A and ![]() ${\mathcal U}$. Then the following statements hold:
${\mathcal U}$. Then the following statements hold:
(i)
 $A|_{\mathcal M}$ is
$A|_{\mathcal M}$ is  ${\mathcal U}|_{\mathcal M}$-commuting.
${\mathcal U}|_{\mathcal M}$-commuting.(ii)
 $\Delta_{rA|_{\mathcal M}}(I_{\mathcal M})=\Delta_{rA}(P_{\mathcal M})|_{\mathcal M}$ for any
$\Delta_{rA|_{\mathcal M}}(I_{\mathcal M})=\Delta_{rA}(P_{\mathcal M})|_{\mathcal M}$ for any  $r\in [0,1]$.
$r\in [0,1]$.(iii) If
 $A\in \textbf{B}^{{\mathcal U}}({\mathcal H})$, then
$A\in \textbf{B}^{{\mathcal U}}({\mathcal H})$, then  $A|_{\mathcal M}\in \textbf{B}^{{\mathcal U}|_{\mathcal M}}({\mathcal M})$.
$A|_{\mathcal M}\in \textbf{B}^{{\mathcal U}|_{\mathcal M}}({\mathcal M})$.(iv) If
 $A\in \textbf{B}^{{\mathcal U}}_{reg}({\mathcal H})$, then
$A\in \textbf{B}^{{\mathcal U}}_{reg}({\mathcal H})$, then  $A|_{\mathcal M}\in \textbf{B}_{reg}^{{\mathcal U}|_{\mathcal M}}({\mathcal M})$ if and only if
$A|_{\mathcal M}\in \textbf{B}_{reg}^{{\mathcal U}|_{\mathcal M}}({\mathcal M})$ if and only if
 \begin{equation*}
\Delta_{rA}(P_{\mathcal M})\geq 0,\qquad r\in [0,1).
\end{equation*}
\begin{equation*}
\Delta_{rA}(P_{\mathcal M})\geq 0,\qquad r\in [0,1).
\end{equation*}If A is pure, then the later condition is equivalent to
 $\Delta_{A}(P_{\mathcal M})\geq 0$.
$\Delta_{A}(P_{\mathcal M})\geq 0$.
Proof. Since ![]() ${\mathcal M}$ is an invariant subspace under A and
${\mathcal M}$ is an invariant subspace under A and ![]() ${\mathcal U}$, item (i) is straightforward and
${\mathcal U}$, item (i) is straightforward and
 \begin{equation*}
\Delta_{rA|_{\mathcal M}}(I_{\mathcal M})=\Delta_{rA}(P_{\mathcal M})|_{\mathcal M},\qquad r\in [0,1).
\end{equation*}
\begin{equation*}
\Delta_{rA|_{\mathcal M}}(I_{\mathcal M})=\Delta_{rA}(P_{\mathcal M})|_{\mathcal M},\qquad r\in [0,1).
\end{equation*} Since item (iii) is clear, we prove (iv). Assume that  $A\in \textbf{B}^{{\mathcal U}}_{reg}({\mathcal H})$, i.e.
$A\in \textbf{B}^{{\mathcal U}}_{reg}({\mathcal H})$, i.e.  $
\Delta_{rA|_{\mathcal M}}(I_{\mathcal M})\geq 0$ for any
$
\Delta_{rA|_{\mathcal M}}(I_{\mathcal M})\geq 0$ for any ![]() $ r\in [0,1)$. Let
$ r\in [0,1)$. Let ![]() $h\in {\mathcal H}$, and consider the orthogonal decomposition
$h\in {\mathcal H}$, and consider the orthogonal decomposition ![]() $h=x+y$, with
$h=x+y$, with ![]() $x\in {\mathcal M}$ and
$x\in {\mathcal M}$ and ![]() $y\in {\mathcal M}^\perp$. Using the fact that
$y\in {\mathcal M}^\perp$. Using the fact that ![]() ${\mathcal M}^\perp$ is invariant subspace under each operator
${\mathcal M}^\perp$ is invariant subspace under each operator ![]() $A_{i,j}^*$, we have
$A_{i,j}^*$, we have
 \begin{equation*}
\begin{split}
\left \lt \Delta_{rA}(P_{\mathcal M})(x+y), x+y\right \gt &=
\left \lt \Delta_{rA}(P_{\mathcal M})x, x+y\right \gt + \left \lt \Delta_{rA}(P_{\mathcal M})y, x+y\right \gt \\
&=\left \lt \Delta_{rA}(P_{\mathcal M})x, x\right \gt +\|y\|^2\geq 0.
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
\left \lt \Delta_{rA}(P_{\mathcal M})(x+y), x+y\right \gt &=
\left \lt \Delta_{rA}(P_{\mathcal M})x, x+y\right \gt + \left \lt \Delta_{rA}(P_{\mathcal M})y, x+y\right \gt \\
&=\left \lt \Delta_{rA}(P_{\mathcal M})x, x\right \gt +\|y\|^2\geq 0.
\end{split}
\end{equation*} Consequently, ![]() $\Delta_{rA}(P_{\mathcal M})\geq 0$ for any
$\Delta_{rA}(P_{\mathcal M})\geq 0$ for any ![]() $ r\in [0,1)$. Conversely, if
$ r\in [0,1)$. Conversely, if ![]() $\Delta_{rA}(P_{\mathcal M})\geq 0$, then it is clear that
$\Delta_{rA}(P_{\mathcal M})\geq 0$, then it is clear that  $\Delta_{rA|_{\mathcal M}}(I_{\mathcal M})\geq 0$. If, in addition, A is pure and
$\Delta_{rA|_{\mathcal M}}(I_{\mathcal M})\geq 0$. If, in addition, A is pure and ![]() $\Delta_A(P_{\mathcal M})\geq 0,$ then, since
$\Delta_A(P_{\mathcal M})\geq 0,$ then, since ![]() $\Phi_{A_1}$ is a positive linear map, we deduce that
$\Phi_{A_1}$ is a positive linear map, we deduce that
 \begin{equation*}\Phi_{A_1}^m \left(id -\Phi_{A_2}\right)\circ \cdots \circ\left(id -\Phi_{A_k}\right)(P_{\mathcal M})\leq \left(id -\Phi_{A_2}\right)\circ \cdots \circ\left(id -\Phi_{A_k}\right)(P_{\mathcal M})\end{equation*}
\begin{equation*}\Phi_{A_1}^m \left(id -\Phi_{A_2}\right)\circ \cdots \circ\left(id -\Phi_{A_k}\right)(P_{\mathcal M})\leq \left(id -\Phi_{A_2}\right)\circ \cdots \circ\left(id -\Phi_{A_k}\right)(P_{\mathcal M})\end{equation*} for any ![]() $m\in {\mathbb N}$. Taking into account that
$m\in {\mathbb N}$. Taking into account that  $\Phi_{A_1}^m (I)\to 0$ as
$\Phi_{A_1}^m (I)\to 0$ as ![]() $m\to \infty$, we deduce that
$m\to \infty$, we deduce that  $\left(id -\Phi_{A_2}\right)\circ \cdots \circ\left(id -\Phi_{A_k}\right)(P_{\mathcal M})\geq 0$. Similarly, taking into account that
$\left(id -\Phi_{A_2}\right)\circ \cdots \circ\left(id -\Phi_{A_k}\right)(P_{\mathcal M})\geq 0$. Similarly, taking into account that ![]() $P_{\mathcal M}\in {\mathcal U}'$, we can use proposition 2.3 and show that
$P_{\mathcal M}\in {\mathcal U}'$, we can use proposition 2.3 and show that  $\left(id -\Phi_{A_1}\right)^{p_1}\circ \cdots \circ\left(id -\Phi_{A_k}\right)^{p_k}(P_{\mathcal M})\geq 0$ for any
$\left(id -\Phi_{A_1}\right)^{p_1}\circ \cdots \circ\left(id -\Phi_{A_k}\right)^{p_k}(P_{\mathcal M})\geq 0$ for any ![]() $p_i\in\{0,1\}$. The later condition implies
$p_i\in\{0,1\}$. The later condition implies ![]() $\Delta_{rA}(P_{\mathcal M})\geq 0$ for any
$\Delta_{rA}(P_{\mathcal M})\geq 0$ for any ![]() $r\in [0,1)$. The proof is very similar to the proof of the implication (ii)
$r\in [0,1)$. The proof is very similar to the proof of the implication (ii)![]() $\implies$ (iii) of proposition 1.2 from [Reference Popescu28]. We include a proof for completeness. Since
$\implies$ (iii) of proposition 1.2 from [Reference Popescu28]. We include a proof for completeness. Since ![]() $\Delta_A(P_{\mathcal M})\geq 0$, we deduce that
$\Delta_A(P_{\mathcal M})\geq 0$, we deduce that ![]() $\Phi_{A_1}(\Delta_{(A_2,\ldots, A_k)}(P_{\mathcal M}))\leq \Delta_{(A_2,\ldots, A_k)}(P_{\mathcal M})$, where
$\Phi_{A_1}(\Delta_{(A_2,\ldots, A_k)}(P_{\mathcal M}))\leq \Delta_{(A_2,\ldots, A_k)}(P_{\mathcal M})$, where
Hence, ![]() $0\leq \Phi_{rA_1}(\Delta_{(A_2,\ldots, A_k)}(P_{\mathcal M})\leq \Delta_{(A_2,\ldots, A_k)}(P_{\mathcal M})$ for any
$0\leq \Phi_{rA_1}(\Delta_{(A_2,\ldots, A_k)}(P_{\mathcal M})\leq \Delta_{(A_2,\ldots, A_k)}(P_{\mathcal M})$ for any ![]() $r\in [0,1)$, and consequently, we have
$r\in [0,1)$, and consequently, we have ![]() $
(id-\Phi_{rA_1})\circ\cdots \circ (id-\Phi_{A_k})(P_{\mathcal M})\geq 0.
$ Since
$
(id-\Phi_{rA_1})\circ\cdots \circ (id-\Phi_{A_k})(P_{\mathcal M})\geq 0.
$ Since ![]() $P_{\mathcal M}\in {\mathcal U}'$, we use proposition 2.3 to deduce that
$P_{\mathcal M}\in {\mathcal U}'$, we use proposition 2.3 to deduce that
A similar argument as above, starting with the inequality ![]() $
(id-\Phi_{A_1})\circ(id-\Phi_{A_3})\circ \cdots \circ (id-\Phi_{A_k})(P_{\mathcal M})\geq 0,
$ leads to
$
(id-\Phi_{A_1})\circ(id-\Phi_{A_3})\circ \cdots \circ (id-\Phi_{A_k})(P_{\mathcal M})\geq 0,
$ leads to ![]() $(id-\Phi_{A_3})\circ\cdots \circ (id-\Phi_{A_k})\circ(id-\Phi_{rA_1})(P_{\mathcal M})\geq 0$. Repeating the argument but starting with the inequality (6.1) shows that
$(id-\Phi_{A_3})\circ\cdots \circ (id-\Phi_{A_k})\circ(id-\Phi_{rA_1})(P_{\mathcal M})\geq 0$. Repeating the argument but starting with the inequality (6.1) shows that
Iterating this process, we conclude that ![]() $\Delta_{rA}(P_{\mathcal M})\geq 0$ for any
$\Delta_{rA}(P_{\mathcal M})\geq 0$ for any ![]() $r \in [0,1)$. The proof is complete.
$r \in [0,1)$. The proof is complete.
Proposition. Let  $A:=(A_1,\ldots, A_k)\in \textbf{B}^{\mathcal U}_{reg}({\mathcal H})$ be a pure k-tuple, and let
$A:=(A_1,\ldots, A_k)\in \textbf{B}^{\mathcal U}_{reg}({\mathcal H})$ be a pure k-tuple, and let ![]() ${\mathcal M}\subset {\mathcal H}$ be a jointly invariant subspace under A and
${\mathcal M}\subset {\mathcal H}$ be a jointly invariant subspace under A and ![]() ${\mathcal U}$. Then, the following statements are equivalent:
${\mathcal U}$. Then, the following statements are equivalent:
(i)
 $A|_{\mathcal M}\in \textbf{B}_{reg}^{{\mathcal U}|_{\mathcal M}}({\mathcal M})$.
$A|_{\mathcal M}\in \textbf{B}_{reg}^{{\mathcal U}|_{\mathcal M}}({\mathcal M})$.(ii)
 ${\mathcal M}$ is a Beurling type invariant subspace, i.e. there are a Hilbert space
${\mathcal M}$ is a Beurling type invariant subspace, i.e. there are a Hilbert space  ${\mathcal E}$, a standard multi-shift
${\mathcal E}$, a standard multi-shift  $\textbf{S}_{\mathcal W}$ of doubly
$\textbf{S}_{\mathcal W}$ of doubly  $I\otimes {\mathcal W}$-commuting pure isometries on the Hilbert space
$I\otimes {\mathcal W}$-commuting pure isometries on the Hilbert space  $ \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal E}$, and a partial isometry
$ \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal E}$, and a partial isometry  $\Psi: \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal E}\to {\mathcal H}$ such that
$\Psi: \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal E}\to {\mathcal H}$ such that
 \begin{equation*}
\Psi(\textbf{S}_{\mathcal W})_{i,s}=A_{i,s}\Psi \ \text{and }\ \Psi(I\otimes W_{i,j}(s,t))=U_{i,j}(s,t)\Psi
\end{equation*}
\begin{equation*}
\Psi(\textbf{S}_{\mathcal W})_{i,s}=A_{i,s}\Psi \ \text{and }\ \Psi(I\otimes W_{i,j}(s,t))=U_{i,j}(s,t)\Psi
\end{equation*}and
 $
{\mathcal M}=\Psi\left(\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal E}\right).
$
$
{\mathcal M}=\Psi\left(\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal E}\right).
$
Proof. The proof follows from proposition 6.9 and corollary 6.4 from [Reference Popescu28].
Theorem Let  $A\in \textbf{B}^{\mathcal U}({\mathcal H})$ be such that
$A\in \textbf{B}^{\mathcal U}({\mathcal H})$ be such that ![]() $\Delta_A(I)$ is a positive trace class operator. If
$\Delta_A(I)$ is a positive trace class operator. If ![]() ${\mathcal M}$ is an invariant subspace under A and
${\mathcal M}$ is an invariant subspace under A and ![]() ${\mathcal U}$ such that
${\mathcal U}$ such that ![]() $\dim {\mathcal M}^\perp \lt \infty$ and
$\dim {\mathcal M}^\perp \lt \infty$ and ![]() $\Delta_A(P_{\mathcal M})\geq 0$, then
$\Delta_A(P_{\mathcal M})\geq 0$, then  $A|_{\mathcal M}\in \textbf{B}^{{\mathcal U}|_{\mathcal M}}({\mathcal M})$ has a positive trace class defect and
$A|_{\mathcal M}\in \textbf{B}^{{\mathcal U}|_{\mathcal M}}({\mathcal M})$ has a positive trace class defect and
 \begin{equation*}
\left|\mathrm{curv}(A)-\mathrm{curv}(A|_{\mathcal M})\right|
\leq \dim {\mathcal M}^\perp\prod_{i=1}^k (n_i-1).
\end{equation*}
\begin{equation*}
\left|\mathrm{curv}(A)-\mathrm{curv}(A|_{\mathcal M})\right|
\leq \dim {\mathcal M}^\perp\prod_{i=1}^k (n_i-1).
\end{equation*}Proof. Since ![]() ${\mathcal M}$ is an invariant subspace under all the operators
${\mathcal M}$ is an invariant subspace under all the operators ![]() $A_{i,s}$, proposition 6.9 shows that
$A_{i,s}$, proposition 6.9 shows that  $\Delta_{A|_{\mathcal M}}(I_{\mathcal M})=\Delta_A(P_{\mathcal M})|_{\mathcal M}:{\mathcal M}\to {\mathcal M}$. Taking into account that
$\Delta_{A|_{\mathcal M}}(I_{\mathcal M})=\Delta_A(P_{\mathcal M})|_{\mathcal M}:{\mathcal M}\to {\mathcal M}$. Taking into account that ![]() ${\mathcal M}^\perp$ is invariant under all
${\mathcal M}^\perp$ is invariant under all ![]() $A_{i,s}^*$, we deduce that
$A_{i,s}^*$, we deduce that ![]() $\Delta_A(P_{\mathcal M})|_{{\mathcal M}^\perp}=0$ and consequently,
$\Delta_A(P_{\mathcal M})|_{{\mathcal M}^\perp}=0$ and consequently,  $\mathrm{trace} [\Delta_{A|_{\mathcal M}}(I_{\mathcal M})]= \mathrm{trace}
[ \Delta_A(P_{\mathcal M})]$. The same proposition shows that if
$\mathrm{trace} [\Delta_{A|_{\mathcal M}}(I_{\mathcal M})]= \mathrm{trace}
[ \Delta_A(P_{\mathcal M})]$. The same proposition shows that if ![]() $\Delta_A(P_{\mathcal M})\geq 0$, then
$\Delta_A(P_{\mathcal M})\geq 0$, then  $\Delta_{A|_{\mathcal M}}(I_{\mathcal M})\geq 0$. On the other hand, taking into account that
$\Delta_{A|_{\mathcal M}}(I_{\mathcal M})\geq 0$. On the other hand, taking into account that ![]() ${\Delta_A}(P_{\mathcal M})={\Delta_A}(I_{\mathcal H})-{\Delta_A}(P_{{\mathcal M}^\perp})$ and
${\Delta_A}(P_{\mathcal M})={\Delta_A}(I_{\mathcal H})-{\Delta_A}(P_{{\mathcal M}^\perp})$ and ![]() $\dim {\mathcal M}^\perp \lt \infty$, we conclude that
$\dim {\mathcal M}^\perp \lt \infty$, we conclude that ![]() $\mathrm{trace}
[ \Delta_A(P_{\mathcal M})] \lt \infty$. This shows that
$\mathrm{trace}
[ \Delta_A(P_{\mathcal M})] \lt \infty$. This shows that ![]() $A|_{\mathcal M}$ is in
$A|_{\mathcal M}$ is in  $\textbf{B}^{{\mathcal U}|_{\mathcal M}}({\mathcal M})$ and has a positive trace class defect. Therefore,
$\textbf{B}^{{\mathcal U}|_{\mathcal M}}({\mathcal M})$ and has a positive trace class defect. Therefore, ![]() $\mathrm{curv}(A|_{\mathcal M})$ exists.
$\mathrm{curv}(A|_{\mathcal M})$ exists.
Using again that ![]() ${\mathcal M}$ is an invariant subspace under all operators
${\mathcal M}$ is an invariant subspace under all operators ![]() $A_{i,s}$, we deduce that
$A_{i,s}$, we deduce that
 \begin{equation*}
\begin{split}
\mathrm{trace}&\left[\left(id -\Phi_{A_1|_{\mathcal M}}^{q_1+1}\right)\circ \cdots \circ\left(id -\Phi_{A_k|_{\mathcal M}}^{q_k+1}\right)(I_{\mathcal M})\right]\\
&= \mathrm{trace}\left[\left(id -\Phi_{A_1}^{q_1+1}\right)\circ \cdots \circ\left(id -\Phi_{A_k}^{q_k+1}\right)(P_{\mathcal M})\right]\\
&= \mathrm{trace}\left[\left(id -\Phi_{A_1}^{q_1+1}\right)\circ \cdots \circ\left(id -\Phi_{A_k}^{q_k+1}\right)(I_{\mathcal H})\right] \\ & \qquad -\mathrm{trace}\left[\left(id -\Phi_{A_1}^{q_1+1}\right)\circ \cdots \circ\left(id -\Phi_{A_k}^{q_k+1}\right)(P_{{\mathcal M}^\perp})\right]\\
&\leq \mathrm{trace}\left[\left(id -\Phi_{A_1}^{q_1+1}\right)\circ \cdots \circ\left(id -\Phi_{A_k}^{q_k+1}\right)(I_{\mathcal H})\right] \\ & \qquad+ (1+n_1^{q_1+1})\cdots (1+n_k^{q_k+1})
\mathrm{trace}\,[P_{{\mathcal M}^\perp}].
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
\mathrm{trace}&\left[\left(id -\Phi_{A_1|_{\mathcal M}}^{q_1+1}\right)\circ \cdots \circ\left(id -\Phi_{A_k|_{\mathcal M}}^{q_k+1}\right)(I_{\mathcal M})\right]\\
&= \mathrm{trace}\left[\left(id -\Phi_{A_1}^{q_1+1}\right)\circ \cdots \circ\left(id -\Phi_{A_k}^{q_k+1}\right)(P_{\mathcal M})\right]\\
&= \mathrm{trace}\left[\left(id -\Phi_{A_1}^{q_1+1}\right)\circ \cdots \circ\left(id -\Phi_{A_k}^{q_k+1}\right)(I_{\mathcal H})\right] \\ & \qquad -\mathrm{trace}\left[\left(id -\Phi_{A_1}^{q_1+1}\right)\circ \cdots \circ\left(id -\Phi_{A_k}^{q_k+1}\right)(P_{{\mathcal M}^\perp})\right]\\
&\leq \mathrm{trace}\left[\left(id -\Phi_{A_1}^{q_1+1}\right)\circ \cdots \circ\left(id -\Phi_{A_k}^{q_k+1}\right)(I_{\mathcal H})\right] \\ & \qquad+ (1+n_1^{q_1+1})\cdots (1+n_k^{q_k+1})
\mathrm{trace}\,[P_{{\mathcal M}^\perp}].
\end{split}
\end{equation*}Hence, we obtain
 \begin{equation*}
\begin{split}
&\left|\frac{\mathrm{trace}\left[\left(id -\Phi_{T_1}^{q_1+1}\right)\circ \cdots \circ\left(id -\Phi_{T_k}^{q_k+1}\right)(I_{\mathcal H})\right]}{{\prod_{i=1}^k(1+n_i+\cdots + n_i^{q_i})}}\right.\\ & \qquad \left. -\frac{\mathrm{trace}\left[\left(id -\Phi_{T_1|_{\mathcal M}}^{q_1+1}\right)\circ \cdots \circ\left(id -\Phi_{T_k|_{\mathcal M}}^{q_k+1}\right)(I_{\mathcal M})\right]}{{\prod_{i=1}^k(1+n_i+\cdots + n_i^{q_i})}}
\right|\\
&\qquad\qquad\leq \frac{(1+n_1^{q_1+1})\cdots (1+n_k^{q_k+1})}{{\prod_{i=1}^k(1+n_i+\cdots + n_i^{q_i})}}\mathrm{trace}\,[P_{{\mathcal M}^\perp}].
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
&\left|\frac{\mathrm{trace}\left[\left(id -\Phi_{T_1}^{q_1+1}\right)\circ \cdots \circ\left(id -\Phi_{T_k}^{q_k+1}\right)(I_{\mathcal H})\right]}{{\prod_{i=1}^k(1+n_i+\cdots + n_i^{q_i})}}\right.\\ & \qquad \left. -\frac{\mathrm{trace}\left[\left(id -\Phi_{T_1|_{\mathcal M}}^{q_1+1}\right)\circ \cdots \circ\left(id -\Phi_{T_k|_{\mathcal M}}^{q_k+1}\right)(I_{\mathcal M})\right]}{{\prod_{i=1}^k(1+n_i+\cdots + n_i^{q_i})}}
\right|\\
&\qquad\qquad\leq \frac{(1+n_1^{q_1+1})\cdots (1+n_k^{q_k+1})}{{\prod_{i=1}^k(1+n_i+\cdots + n_i^{q_i})}}\mathrm{trace}\,[P_{{\mathcal M}^\perp}].
\end{split}
\end{equation*} If ![]() $n_i=1$ for some
$n_i=1$ for some ![]() $i\in\{1,\ldots, k\}$, an application of corollary 3.4 shows that
$i\in\{1,\ldots, k\}$, an application of corollary 3.4 shows that ![]() $\mathrm{curv}({A})=\mathrm{curv}({A}|_{\mathcal M})$. On the other hand, if all
$\mathrm{curv}({A})=\mathrm{curv}({A}|_{\mathcal M})$. On the other hand, if all ![]() $n_i\geq 2$, then, using the same corollary, we obtain the inequality in the theorem. The proof is complete.
$n_i\geq 2$, then, using the same corollary, we obtain the inequality in the theorem. The proof is complete.
Let ![]() $A:=(A_1,\ldots, A_k)$ be an element in the
$A:=(A_1,\ldots, A_k)$ be an element in the ![]() ${\mathcal U}$-twisted polyball
${\mathcal U}$-twisted polyball  $ \textbf{B}^{\mathcal U}({\mathcal H})$ such that
$ \textbf{B}^{\mathcal U}({\mathcal H})$ such that ![]() $\Delta_A(I)$ is a positive trace class operator. If
$\Delta_A(I)$ is a positive trace class operator. If ![]() ${\mathcal M}$ is an invariant subspace under A and
${\mathcal M}$ is an invariant subspace under A and ![]() ${\mathcal U}$, we introduce the multiplicity of
${\mathcal U}$, we introduce the multiplicity of ![]() ${\mathcal M}$ with respect to A to be
${\mathcal M}$ with respect to A to be
 \begin{equation*}
m_A({\mathcal M}):= \lim_{(q_1,\ldots, q_k)\in {\mathbb Z}_+^k} \frac{
\mathrm{trace\,}\left[ P_{\mathcal M} K_A^* (P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal H})K_A\right]}{\mathrm{trace\,}[P_{(q_1,\ldots, q_k)}]}.
\end{equation*}
\begin{equation*}
m_A({\mathcal M}):= \lim_{(q_1,\ldots, q_k)\in {\mathbb Z}_+^k} \frac{
\mathrm{trace\,}\left[ P_{\mathcal M} K_A^* (P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal H})K_A\right]}{\mathrm{trace\,}[P_{(q_1,\ldots, q_k)}]}.
\end{equation*} A close look at the proof of theorem 6.1 reveals that one can replace the standard multi-shift S with A and the corresponding proof holds true showing that ![]() $m_A({\mathcal M})$ exists. Moreover, one can obtain analogues of the asymptotic formulas from theorem 6.1 in the new setting and prove that the following index type formula:
$m_A({\mathcal M})$ exists. Moreover, one can obtain analogues of the asymptotic formulas from theorem 6.1 in the new setting and prove that the following index type formula:
Note that if ![]() ${\mathcal M}_1$ and
${\mathcal M}_1$ and ![]() ${\mathcal M}_2$ are orthogonal invariant subspaces under A and
${\mathcal M}_2$ are orthogonal invariant subspaces under A and ![]() ${\mathcal U}$, then
${\mathcal U}$, then
We remark that if ![]() $A=\textbf{S}$, then
$A=\textbf{S}$, then ![]() $m_\textbf{S}({\mathcal M})=m({\mathcal M})$. Indeed, this is due to the fact that
$m_\textbf{S}({\mathcal M})=m({\mathcal M})$. Indeed, this is due to the fact that
 \begin{equation*}
K_\textbf{S}^* (P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal H})K_\textbf{S}=\Phi_{\textbf{S}_1}^{q_1}\circ \cdots \circ \Phi_{\textbf{S}_k}^{q_k}({\Delta_\textbf{S}}(I))=P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal H}.
\end{equation*}
\begin{equation*}
K_\textbf{S}^* (P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal H})K_\textbf{S}=\Phi_{\textbf{S}_1}^{q_1}\circ \cdots \circ \Phi_{\textbf{S}_k}^{q_k}({\Delta_\textbf{S}}(I))=P_{(q_1,\ldots, q_k)}\otimes I_{\mathcal H}.
\end{equation*}7. The range of the curvature and multiplicity invariants
In this section, we determine the range of the curvature and the multiplicity invariants. If ![]() $(n_1,\ldots, n_k)\in {\mathbb N}^k$ is such that
$(n_1,\ldots, n_k)\in {\mathbb N}^k$ is such that ![]() $n_j\geq 2$ for some j, we prove that the range of the curvature over the pure elements in the
$n_j\geq 2$ for some j, we prove that the range of the curvature over the pure elements in the ![]() ${\mathcal U}$-twisted polyballs and the range of the multiplicity invariant coincide with
${\mathcal U}$-twisted polyballs and the range of the multiplicity invariant coincide with ![]() $[0, \infty)$. We also show that the range of the curvature restricted to the class of doubly
$[0, \infty)$. We also show that the range of the curvature restricted to the class of doubly ![]() ${\mathcal U}$-commuting row isometries with trace class defect operator is
${\mathcal U}$-commuting row isometries with trace class defect operator is ![]() ${\mathbb Z}_+$.
${\mathbb Z}_+$.
Let ![]() $S:=(S_1,\ldots, S_k)$ with
$S:=(S_1,\ldots, S_k)$ with ![]() $S_i:=[S_{i,1}\cdots S_{i,n_i}]$ be the standard multi-shift on
$S_i:=[S_{i,1}\cdots S_{i,n_i}]$ be the standard multi-shift on  $\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)$ associated with
$\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)$ associated with ![]() ${\mathcal U}=\{1_{\mathbb C}\}$, and let
${\mathcal U}=\{1_{\mathbb C}\}$, and let ![]() $\textbf{S}:=(\textbf{S}_1,\ldots, \textbf{S}_k)$ with
$\textbf{S}:=(\textbf{S}_1,\ldots, \textbf{S}_k)$ with ![]() $\textbf{S}_i:=[\textbf{S}_{i,1}\cdots \textbf{S}_{i,n_i}]$ be the standard k-tuple of doubly
$\textbf{S}_i:=[\textbf{S}_{i,1}\cdots \textbf{S}_{i,n_i}]$ be the standard k-tuple of doubly ![]() $I\otimes{\mathcal U}$-commuting row isometries on the Hilbert space
$I\otimes{\mathcal U}$-commuting row isometries on the Hilbert space  $\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal H}$. For each
$\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal H}$. For each ![]() $i\in \{1,\ldots, k\}$ and
$i\in \{1,\ldots, k\}$ and ![]() $s\in \{1,\ldots, n_i\}$, we define the block diagonal operator
$s\in \{1,\ldots, n_i\}$, we define the block diagonal operator  $D_{i,s}\in B(\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal H})$ by setting
$D_{i,s}\in B(\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal H})$ by setting
and ![]() $D_{i,s}=I$ if i = 1. Note that
$D_{i,s}=I$ if i = 1. Note that ![]() $\textbf{S}_{i,s}=(S_{i,s}\otimes I_{\mathcal H})D_{i,s}$.
$\textbf{S}_{i,s}=(S_{i,s}\otimes I_{\mathcal H})D_{i,s}$.
Lemma 7.1. Let  $\Omega\subset {\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+$, and let
$\Omega\subset {\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+$, and let  ${\mathcal M}_\Omega\subset \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)$ be the smallest invariant subspace under the multi-shift S generated by
${\mathcal M}_\Omega\subset \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)$ be the smallest invariant subspace under the multi-shift S generated by ![]() $\{\chi_{\bf \alpha}: \ \bf\alpha\in \Omega\}$. If
$\{\chi_{\bf \alpha}: \ \bf\alpha\in \Omega\}$. If ![]() ${\mathcal N}\subset {\mathcal H}$ is an invariant subspace under
${\mathcal N}\subset {\mathcal H}$ is an invariant subspace under ![]() $\{U_{i,j}(s,t)\}_{(i,j,s,t)\in \Gamma_-}$, where
$\{U_{i,j}(s,t)\}_{(i,j,s,t)\in \Gamma_-}$, where ![]() $\Gamma_-:=\{(i,j,s,t)\in \Gamma, i \gt j\}$, then
$\Gamma_-:=\{(i,j,s,t)\in \Gamma, i \gt j\}$, then ![]() ${\mathcal M}_\Omega\otimes {\mathcal N}$ is an invariant subspace under the multi-shift S.
${\mathcal M}_\Omega\otimes {\mathcal N}$ is an invariant subspace under the multi-shift S.
Proof. Note that
 \begin{equation*}{\mathcal M}_\Omega=\overline{\mathrm{span}}\{\chi_{(\beta_1\alpha_1,\ldots, \beta_k\alpha_k)}:\
\bf\alpha\in \Omega, \bf\beta \in {\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+\}
\end{equation*}
\begin{equation*}{\mathcal M}_\Omega=\overline{\mathrm{span}}\{\chi_{(\beta_1\alpha_1,\ldots, \beta_k\alpha_k)}:\
\bf\alpha\in \Omega, \bf\beta \in {\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+\}
\end{equation*} and if ![]() $h\in {\mathcal N}$, then
$h\in {\mathcal N}$, then
 \begin{align*}
& D_{i,s}(\chi_{(\beta_1\alpha_1,\ldots, \beta_k\alpha_k)}\otimes h)=
\chi_{(\beta_1\alpha_1,\ldots, \beta_k\alpha_k)}\otimes \bf U_{i,1}(s,\beta_1\alpha_1)\cdots \\ & \qquad \bf U_{i,i-1}(s,\beta_{i-1}\alpha_{i-1})h\in {\mathcal M}_\Omega\otimes {\mathcal L}.
\end{align*}
\begin{align*}
& D_{i,s}(\chi_{(\beta_1\alpha_1,\ldots, \beta_k\alpha_k)}\otimes h)=
\chi_{(\beta_1\alpha_1,\ldots, \beta_k\alpha_k)}\otimes \bf U_{i,1}(s,\beta_1\alpha_1)\cdots \\ & \qquad \bf U_{i,i-1}(s,\beta_{i-1}\alpha_{i-1})h\in {\mathcal M}_\Omega\otimes {\mathcal L}.
\end{align*} Since ![]() $(S_{i,s}\otimes I)({\mathcal M}_\Omega\otimes {\mathcal L})\subset {\mathcal M}_\Omega\otimes {\mathcal L}$ and
$(S_{i,s}\otimes I)({\mathcal M}_\Omega\otimes {\mathcal L})\subset {\mathcal M}_\Omega\otimes {\mathcal L}$ and ![]() $\textbf{S}_{i,s}=(S_{i,s}\otimes I_{\mathcal H})D_{i,s}$, the proof is complete.
$\textbf{S}_{i,s}=(S_{i,s}\otimes I_{\mathcal H})D_{i,s}$, the proof is complete.
Theorem 7.2 Let ![]() $(n_1,\ldots, n_k)\in {\mathbb N}^k$ be such that
$(n_1,\ldots, n_k)\in {\mathbb N}^k$ be such that ![]() $n_j\geq 2$ for some j. Then, the following statements hold:
$n_j\geq 2$ for some j. Then, the following statements hold:
(i) For any
 $t\in [0,1]$, there is an invariant subspace
$t\in [0,1]$, there is an invariant subspace  ${\mathcal M}\subset \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)$ of the z-twisted multi-shift
${\mathcal M}\subset \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)$ of the z-twisted multi-shift  $\mathbf{S_z}$ on
$\mathbf{S_z}$ on  $\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)$ such that
$\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)$ such that
 \begin{equation*}
\mathrm{curv}(P_{{\mathcal M}^\perp} \textbf{S}_\textbf{z}|_{{\mathcal M}^\perp})=t\quad \text{and } \quad m({\mathcal M})=1-t.
\end{equation*}
\begin{equation*}
\mathrm{curv}(P_{{\mathcal M}^\perp} \textbf{S}_\textbf{z}|_{{\mathcal M}^\perp})=t\quad \text{and } \quad m({\mathcal M})=1-t.
\end{equation*}(ii) For any
 $t\in [0,m]$, there exists a pure element A in the
$t\in [0,m]$, there exists a pure element A in the  ${\mathcal U}$-twisted polyball such that
${\mathcal U}$-twisted polyball such that  $\mathrm{rank}\, A=m$ and
$\mathrm{rank}\, A=m$ and  $\mathrm{curv}(A)=t$.
$\mathrm{curv}(A)=t$.(iii) The range of the curvature on the
 ${\mathcal U}$-twisted polyballs is
${\mathcal U}$-twisted polyballs is  $[0,\infty)$.
$[0,\infty)$.(iv)
 $P_{{\mathcal M}^\perp} \textbf{S}_\textbf{z}|_{{\mathcal M}^\perp}$ is unitarily equivalent to
$P_{{\mathcal M}^\perp} \textbf{S}_\textbf{z}|_{{\mathcal M}^\perp}$ is unitarily equivalent to  $P_{{\mathcal M}^\perp} \textbf{S}_{\textbf{z}'}|_{{\mathcal M}^\perp}$ if and only if
$P_{{\mathcal M}^\perp} \textbf{S}_{\textbf{z}'}|_{{\mathcal M}^\perp}$ if and only if  $ \textbf{z}=\textbf{z}'$.
$ \textbf{z}=\textbf{z}'$.
Proof. Fix ![]() $a\in (0,1)$ and consider its nj-arry representation
$a\in (0,1)$ and consider its nj-arry representation  $a=\sum_{p=1}^N \frac{d_p}{n_j^{k_p}}$, where
$a=\sum_{p=1}^N \frac{d_p}{n_j^{k_p}}$, where  $\{k_p\}_{p=1}^N$ is a sequence of natural numbers with
$\{k_p\}_{p=1}^N$ is a sequence of natural numbers with ![]() $1\leq k_1 \lt k_2 \lt \cdots$,
$1\leq k_1 \lt k_2 \lt \cdots$, ![]() $N\in {\mathbb N}$ or
$N\in {\mathbb N}$ or ![]() $N=\infty$, and
$N=\infty$, and ![]() $d_p\in\{1,2,\ldots, n_j-1\}$. Consider the subsets of
$d_p\in\{1,2,\ldots, n_j-1\}$. Consider the subsets of  ${\mathbb F}_{n_j}^+$ defined by setting
${\mathbb F}_{n_j}^+$ defined by setting
 \begin{equation*}
\begin{split}
\Omega_1&:=\left\{(g_1^j)^{k_1},\ldots, (g_{d_1}^j)^{k_1}\right\},\\
\Omega_p&:=\left\{(g_1^j)^{k_p-k_{p-1}}(g_{n_j}^j)^{k_{p-1}}, (g_2^j)^{k_p-k_{p-1}}(g_{n_j}^j)^{k_{p-1}},\ldots, (g_{d_p}^j)^{k_p-k_{p-1}}(g_{n_j}^j)^{k_{p-1}}\right\}, \\ & \qquad \quad p=2,3,\ldots, N,
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
\Omega_1&:=\left\{(g_1^j)^{k_1},\ldots, (g_{d_1}^j)^{k_1}\right\},\\
\Omega_p&:=\left\{(g_1^j)^{k_p-k_{p-1}}(g_{n_j}^j)^{k_{p-1}}, (g_2^j)^{k_p-k_{p-1}}(g_{n_j}^j)^{k_{p-1}},\ldots, (g_{d_p}^j)^{k_p-k_{p-1}}(g_{n_j}^j)^{k_{p-1}}\right\}, \\ & \qquad \quad p=2,3,\ldots, N,
\end{split}
\end{equation*}and let
 \begin{equation*}
{\mathcal M}:=\overline{\mathrm{span}}\left\{\chi_{(\alpha_1,\ldots,\alpha_k)}:\ \alpha_j\in \cup_{p=1}^N \Omega_p \ \text{and }\ \alpha_i\in {\mathbb F}_{n_i}^+ \text{if } i\neq j \right\}.
\end{equation*}
\begin{equation*}
{\mathcal M}:=\overline{\mathrm{span}}\left\{\chi_{(\alpha_1,\ldots,\alpha_k)}:\ \alpha_j\in \cup_{p=1}^N \Omega_p \ \text{and }\ \alpha_i\in {\mathbb F}_{n_i}^+ \text{if } i\neq j \right\}.
\end{equation*} Due to lemma 7.1, ![]() ${\mathcal M}$ is an invariant subspace under the z-twisted multi-shift
${\mathcal M}$ is an invariant subspace under the z-twisted multi-shift ![]() $\mathbf{S_z}$. Assume now that
$\mathbf{S_z}$. Assume now that ![]() $k_p\leq q_j \lt k_{p+1}$ and
$k_p\leq q_j \lt k_{p+1}$ and ![]() $q_i\in {\mathbb Z}_+$ if i ≠ j. Note that
$q_i\in {\mathbb Z}_+$ if i ≠ j. Note that
 \begin{equation*}
\begin{split}
&\frac{\mathrm{trace\,}\left[P_{{\mathcal M}}P_{(q_1,\ldots, q_k)} \right]}{\mathrm{trace\,}\left[P_{(q_1,\ldots, q_k)}\right]} \\
& \qquad\qquad =\frac{1}{n_1^{q_1}\cdots n_k^{q_k}}
\sum_{(\alpha_1,\ldots,\alpha_k)\in {\mathbb F}_{n_1}^+\times\cdots\times {\mathbb F}_{n_k}^+}
\left \lt P_{{\mathcal M}}P_{(q_1,\ldots, q_k)} \chi_{(\alpha_1,\ldots,\alpha_k)},
\chi_{(\alpha_1,\ldots,\alpha_k)} \right \gt \\
&\qquad\qquad=
\frac{1}{n_1^{q_1}\cdots n_k^{q_k}}
\sum_{{(\alpha_1,\ldots,\alpha_k)\in {\mathbb F}_{n_1}^+\times\cdots\times {\mathbb F}_{n_k}^+}\atop{|\alpha_1|=q_1,\ldots, |\alpha_k|=q_k}}
\| P_{{\mathcal M}}
\chi_{(\alpha_1,\ldots,\alpha_k)}\|^2\\
&=\frac{d_1 n_j^{q_j-k_1}\left(\prod_{i \in\{1,\ldots,k\}\backslash\{j\}}n_i^{q_i}\right)+\cdots +
d_p n_j^{q_j-k_p}\left(\prod_{i \in\{1,\ldots,k\}\backslash\{j\}} n_i^{q_j}\right)} {n_1^{q_1}\cdots n_k^{q_k}}
\\
&= \frac{d_1}{n_j^{k_1}}+\cdots + \frac{d_p}{n_j^{k_p}}.
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
&\frac{\mathrm{trace\,}\left[P_{{\mathcal M}}P_{(q_1,\ldots, q_k)} \right]}{\mathrm{trace\,}\left[P_{(q_1,\ldots, q_k)}\right]} \\
& \qquad\qquad =\frac{1}{n_1^{q_1}\cdots n_k^{q_k}}
\sum_{(\alpha_1,\ldots,\alpha_k)\in {\mathbb F}_{n_1}^+\times\cdots\times {\mathbb F}_{n_k}^+}
\left \lt P_{{\mathcal M}}P_{(q_1,\ldots, q_k)} \chi_{(\alpha_1,\ldots,\alpha_k)},
\chi_{(\alpha_1,\ldots,\alpha_k)} \right \gt \\
&\qquad\qquad=
\frac{1}{n_1^{q_1}\cdots n_k^{q_k}}
\sum_{{(\alpha_1,\ldots,\alpha_k)\in {\mathbb F}_{n_1}^+\times\cdots\times {\mathbb F}_{n_k}^+}\atop{|\alpha_1|=q_1,\ldots, |\alpha_k|=q_k}}
\| P_{{\mathcal M}}
\chi_{(\alpha_1,\ldots,\alpha_k)}\|^2\\
&=\frac{d_1 n_j^{q_j-k_1}\left(\prod_{i \in\{1,\ldots,k\}\backslash\{j\}}n_i^{q_i}\right)+\cdots +
d_p n_j^{q_j-k_p}\left(\prod_{i \in\{1,\ldots,k\}\backslash\{j\}} n_i^{q_j}\right)} {n_1^{q_1}\cdots n_k^{q_k}}
\\
&= \frac{d_1}{n_j^{k_1}}+\cdots + \frac{d_p}{n_j^{k_p}}.
\end{split}
\end{equation*}Hence and using corollary 6.2, we deduce that
 \begin{equation*}
\begin{split}
\mathrm{curv}(P_{{\mathcal M}^\perp} \textbf{S}_\textbf{z}|_{{\mathcal M}^\perp})=1-\lim_{q_1,\ldots,q_k\to\infty}
\frac{\mathrm{trace\,}\left[P_{{\mathcal M}}P_{(q_1,\ldots, q_k)} \right]}{\mathrm{trace\,}\left[P_{(q_1,\ldots, q_k)}\right]} = 1-\sum_{p=1}^N \frac{d_p}{n_j^{k_p}}=1-a.
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
\mathrm{curv}(P_{{\mathcal M}^\perp} \textbf{S}_\textbf{z}|_{{\mathcal M}^\perp})=1-\lim_{q_1,\ldots,q_k\to\infty}
\frac{\mathrm{trace\,}\left[P_{{\mathcal M}}P_{(q_1,\ldots, q_k)} \right]}{\mathrm{trace\,}\left[P_{(q_1,\ldots, q_k)}\right]} = 1-\sum_{p=1}^N \frac{d_p}{n_j^{k_p}}=1-a.
\end{split}
\end{equation*} On the other hand, we note that ![]() $ \mathrm{curv}(S_\textbf{z})=1$ (see corollary 5.6) and
$ \mathrm{curv}(S_\textbf{z})=1$ (see corollary 5.6) and ![]() $\mathrm{curv}(A)=0$ if A is the
$\mathrm{curv}(A)=0$ if A is the ![]() ${\mathcal U}$-twisted polyball over a finite dimensional Hilbert space. This proves item (i) of the theorem. To prove items (ii) and (iii), we use part (i), consider direct sums of
${\mathcal U}$-twisted polyball over a finite dimensional Hilbert space. This proves item (i) of the theorem. To prove items (ii) and (iii), we use part (i), consider direct sums of ![]() ${\mathcal U}$-twisted polyballs and apply corollary 2.9.
${\mathcal U}$-twisted polyballs and apply corollary 2.9.
Now, we prove item (iv). Since ![]() ${\mathcal M}^\perp$ is a cyclic subspace
${\mathcal M}^\perp$ is a cyclic subspace ![]() $\textbf{S}_\textbf{z}$, the minimal isometric dilation of
$\textbf{S}_\textbf{z}$, the minimal isometric dilation of ![]() $P_{{\mathcal M}^\perp} \textbf{S}_\textbf{z}|_{{\mathcal M}^\perp}$ is
$P_{{\mathcal M}^\perp} \textbf{S}_\textbf{z}|_{{\mathcal M}^\perp}$ is ![]() $\textbf{S}_\textbf{z}$. If
$\textbf{S}_\textbf{z}$. If ![]() $P_{{\mathcal M}^\perp} \textbf{S}_\textbf{z}|_{{\mathcal M}^\perp}$ is unitarily equivalent to
$P_{{\mathcal M}^\perp} \textbf{S}_\textbf{z}|_{{\mathcal M}^\perp}$ is unitarily equivalent to ![]() $P_{{\mathcal M}^\perp} \textbf{S}_{\textbf{z}'}|_{{\mathcal M}^\perp}$, then their minimal isometric dilations
$P_{{\mathcal M}^\perp} \textbf{S}_{\textbf{z}'}|_{{\mathcal M}^\perp}$, then their minimal isometric dilations ![]() $\textbf{S}_\textbf{z}$ and
$\textbf{S}_\textbf{z}$ and ![]() $\textbf{S}_{\textbf{z}'}$, respectively, are unitarily equivalent. Using corollary 4.2, we complete the proof.
$\textbf{S}_{\textbf{z}'}$, respectively, are unitarily equivalent. Using corollary 4.2, we complete the proof.
What is the range of the curvature in the particular case when ![]() $n_1=\cdots=n_k=1$ ? At the moment, we know that the curvature invariant takes all the values in
$n_1=\cdots=n_k=1$ ? At the moment, we know that the curvature invariant takes all the values in ![]() ${\mathbb Z}_+$. Whether these are the only values remains to be seen. We mention that, when
${\mathbb Z}_+$. Whether these are the only values remains to be seen. We mention that, when ![]() ${\mathcal U}=\{1\}$, then according to [Reference Fang9], the curvature takes only integer values.
${\mathcal U}=\{1\}$, then according to [Reference Fang9], the curvature takes only integer values.
Corollary. The range of the ![]() $*$-curvature on the
$*$-curvature on the ![]() ${\mathcal U}$-twisted polyballs is
${\mathcal U}$-twisted polyballs is ![]() $[0,\infty)$.
$[0,\infty)$.
We remark that, due to corollary 6.2, if  ${\mathcal M}\subset \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)$ is a proper invariant subspace of the z-twisted multi-shift
${\mathcal M}\subset \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)$ is a proper invariant subspace of the z-twisted multi-shift ![]() $\mathbf{S_z}$ with
$\mathbf{S_z}$ with ![]() $\dim {\mathcal M}^\perp \lt \infty$, then
$\dim {\mathcal M}^\perp \lt \infty$, then
However, we have the following result when ![]() $\dim {\mathcal M}^\perp=\infty$.
$\dim {\mathcal M}^\perp=\infty$.
Proposition 7.4. If ![]() $(n_1,\ldots, n_k)\in {\mathbb N}^k$ with
$(n_1,\ldots, n_k)\in {\mathbb N}^k$ with ![]() $n_j\geq 2$ for some
$n_j\geq 2$ for some ![]() $j\in \{1,\ldots, k\}$, then there exist invariant subspaces
$j\in \{1,\ldots, k\}$, then there exist invariant subspaces  ${\mathcal M}\subset \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)$ of the z-twisted multi-shift
${\mathcal M}\subset \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)$ of the z-twisted multi-shift ![]() $\mathbf{S_z}$ with
$\mathbf{S_z}$ with ![]() $\dim {\mathcal M}^\perp=\infty$ such that
$\dim {\mathcal M}^\perp=\infty$ such that ![]() $
\mathrm{curv}(P_{{\mathcal M}^\perp} \textbf{S}_\textbf{z}|_{{\mathcal M}^\perp})=0.
$
$
\mathrm{curv}(P_{{\mathcal M}^\perp} \textbf{S}_\textbf{z}|_{{\mathcal M}^\perp})=0.
$
Proof. Let
 \begin{equation*}
{\mathcal S}:\overline{\mathrm{span}}\left\{\chi_{g_0^1,\ldots, g_0^{j-1}, (g_1^j)^p, g_0^{j+1},\ldots, g_0^k)}:\ p\in {\mathbb Z}^+\right\},
\end{equation*}
\begin{equation*}
{\mathcal S}:\overline{\mathrm{span}}\left\{\chi_{g_0^1,\ldots, g_0^{j-1}, (g_1^j)^p, g_0^{j+1},\ldots, g_0^k)}:\ p\in {\mathbb Z}^+\right\},
\end{equation*} and note that ![]() ${\mathcal M}:={\mathcal S}^\perp$ is infinite codimensional and invariant under
${\mathcal M}:={\mathcal S}^\perp$ is infinite codimensional and invariant under ![]() $\mathbf{S_z}$. Due to corollary 6.2, we have
$\mathbf{S_z}$. Due to corollary 6.2, we have
 \begin{equation*}
\begin{split}
&\mathrm{curv}(P_{{\mathcal M}^\perp} \textbf{S}_\textbf{z}|_{{\mathcal M}^\perp})\\
&\qquad=
1-\lim_{q_1,\ldots, q_k\to\infty} \frac{1}{n_1^{q_1}\cdots n_k^{q_k}}
\sum_{(\alpha_1,\ldots,\alpha_k)\in {\mathbb F}_{n_1}^+\times\cdots\times {\mathbb F}_{n_k}^+}\\ & \qquad\qquad
\left \lt P_{{\mathcal M}}P_{(q_1,\ldots, q_k)} \chi_{(\alpha_1,\ldots,\alpha_k)},
\chi_{(\alpha_1,\ldots,\alpha_k)} \right \gt \\
&\qquad=
1-\lim_{q_1,\ldots, q_k\to\infty}\frac{1}{n_1^{q_1}\cdots n_k^{q_k}}
\sum_{{(\alpha_1,\ldots,\alpha_k)\in {\mathbb F}_{n_1}^+\times\cdots\times {\mathbb F}_{n_k}^+}\atop{|\alpha_1|=q_1,\ldots, |\alpha_k|=q_k}}
\| P_{{\mathcal M}}
\chi_{(\alpha_1,\ldots,\alpha_k)}\|^2\\
&\qquad=
1-\lim_{q_1,\ldots, q_k\to\infty} \frac{n_1^{q_1}\cdots n_{j-1}^{q_{j-1}}(n_j^{q_j}-1)
n_{j+1}^{q_{j+1}}\cdots n_k^{q_k}
}
{n_1^{q_1}\cdots n_k^{q_k}} =0.
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
&\mathrm{curv}(P_{{\mathcal M}^\perp} \textbf{S}_\textbf{z}|_{{\mathcal M}^\perp})\\
&\qquad=
1-\lim_{q_1,\ldots, q_k\to\infty} \frac{1}{n_1^{q_1}\cdots n_k^{q_k}}
\sum_{(\alpha_1,\ldots,\alpha_k)\in {\mathbb F}_{n_1}^+\times\cdots\times {\mathbb F}_{n_k}^+}\\ & \qquad\qquad
\left \lt P_{{\mathcal M}}P_{(q_1,\ldots, q_k)} \chi_{(\alpha_1,\ldots,\alpha_k)},
\chi_{(\alpha_1,\ldots,\alpha_k)} \right \gt \\
&\qquad=
1-\lim_{q_1,\ldots, q_k\to\infty}\frac{1}{n_1^{q_1}\cdots n_k^{q_k}}
\sum_{{(\alpha_1,\ldots,\alpha_k)\in {\mathbb F}_{n_1}^+\times\cdots\times {\mathbb F}_{n_k}^+}\atop{|\alpha_1|=q_1,\ldots, |\alpha_k|=q_k}}
\| P_{{\mathcal M}}
\chi_{(\alpha_1,\ldots,\alpha_k)}\|^2\\
&\qquad=
1-\lim_{q_1,\ldots, q_k\to\infty} \frac{n_1^{q_1}\cdots n_{j-1}^{q_{j-1}}(n_j^{q_j}-1)
n_{j+1}^{q_{j+1}}\cdots n_k^{q_k}
}
{n_1^{q_1}\cdots n_k^{q_k}} =0.
\end{split}
\end{equation*}The proof is complete.
Theorem Let ![]() $V:=(V_1,\ldots, V_k)$ with
$V:=(V_1,\ldots, V_k)$ with ![]() $V_i:=[V_{i,1}\cdots V_{i,n_i}]$ and
$V_i:=[V_{i,1}\cdots V_{i,n_i}]$ and ![]() $V_{i,s}\in B({\mathcal H})$ be a k-tuple of doubly
$V_{i,s}\in B({\mathcal H})$ be a k-tuple of doubly ![]() ${\mathcal U}$-commuting row isometries with a trace class defect operator. Then the following statements hold:
${\mathcal U}$-commuting row isometries with a trace class defect operator. Then the following statements hold:
(i)
 $\mathrm{curv} (V)=\mathrm{trace} [\Delta_V(I)]=\mathrm{rank}\, \Delta_V(I)$ and
$\mathrm{curv} (V)=\mathrm{trace} [\Delta_V(I)]=\mathrm{rank}\, \Delta_V(I)$ and
 \begin{equation*}
\mathrm{curv} (V)\neq 0 \ \text{if and only if }\ \bigcap_{{i\in \{1,\ldots, k\}}\atop{s\in \{1,\ldots, n_i\}}} \ker V_{i,s}^*\neq \{0\}.
\end{equation*}
\begin{equation*}
\mathrm{curv} (V)\neq 0 \ \text{if and only if }\ \bigcap_{{i\in \{1,\ldots, k\}}\atop{s\in \{1,\ldots, n_i\}}} \ker V_{i,s}^*\neq \{0\}.
\end{equation*}(ii) For each
 $m\in {\mathbb Z}_+$,
$m\in {\mathbb Z}_+$,
 \begin{equation*}\mathrm{curv} (V)=m\ \text{ if and only if } \ \dim \bigcap_{{i\in \{1,\ldots, k\}}\atop{s\in \{1,\ldots, n_i\}}} \ker V_{i,s}^*=m.
\end{equation*}
\begin{equation*}\mathrm{curv} (V)=m\ \text{ if and only if } \ \dim \bigcap_{{i\in \{1,\ldots, k\}}\atop{s\in \{1,\ldots, n_i\}}} \ker V_{i,s}^*=m.
\end{equation*}(iii) If
 $m\in {\mathbb Z}_+$, there is a k-tuple V of doubly
$m\in {\mathbb Z}_+$, there is a k-tuple V of doubly  ${\mathcal U}$-commuting row isometries such that
${\mathcal U}$-commuting row isometries such that  $\mathrm{curv} (V)=m$.
$\mathrm{curv} (V)=m$.(iv) If
 $\mathrm{curv} (V)\neq 0$ and
$\mathrm{curv} (V)\neq 0$ and  $n_j\geq 2$ for some
$n_j\geq 2$ for some  $j\in \{1,\ldots, k\}$, then for any
$j\in \{1,\ldots, k\}$, then for any  $t\in [0, \mathrm{curv} (V)]$, there is an invariant subspace
$t\in [0, \mathrm{curv} (V)]$, there is an invariant subspace  ${\mathcal M}\subset {\mathcal H}$ under V and
${\mathcal M}\subset {\mathcal H}$ under V and  ${\mathcal U}$ such that
${\mathcal U}$ such that  $\mathrm{curv} (P_{{\mathcal M}^\perp}V|_{{\mathcal M}^\perp})=t$.
$\mathrm{curv} (P_{{\mathcal M}^\perp}V|_{{\mathcal M}^\perp})=t$.
Proof. According to the Wold decomposition of theorem 1.5 from [Reference Popescu27], there exist 2k subspaces ![]() $\{{\mathcal H}_\Omega\}_{\Omega\subset \{1,\ldots, k\}}$ (some of them may be trivial) such that
$\{{\mathcal H}_\Omega\}_{\Omega\subset \{1,\ldots, k\}}$ (some of them may be trivial) such that ![]() ${\mathcal K}$ admits a unique orthogonal decomposition
${\mathcal K}$ admits a unique orthogonal decomposition
 \begin{equation*}
{\mathcal H}=\bigoplus_{\Omega\subset \{1,\ldots, k\}} {\mathcal H}_\Omega
\end{equation*}
\begin{equation*}
{\mathcal H}=\bigoplus_{\Omega\subset \{1,\ldots, k\}} {\mathcal H}_\Omega
\end{equation*} with the property that, for each subset ![]() $\Omega\subset \{1,\ldots, k\}$,
$\Omega\subset \{1,\ldots, k\}$,
(i) the subspace
 ${\mathcal H}_\Omega$ is reducing for all the isometries
${\mathcal H}_\Omega$ is reducing for all the isometries  $V_{i,m}$, where
$V_{i,m}$, where  $i\in \{1,\ldots, k\}$ and
$i\in \{1,\ldots, k\}$ and  $m\in \{1,\ldots, n_i\}$;
$m\in \{1,\ldots, n_i\}$;(ii) if
 $i\in \Omega$, then
$i\in \Omega$, then  $V_i|_{{\mathcal H}_\Omega}:=[V_{i,1}|_{{\mathcal H}_\Omega}\cdots V_{i,n_i}|_{{\mathcal K}_\Omega}]$ is a pure row isometry;
$V_i|_{{\mathcal H}_\Omega}:=[V_{i,1}|_{{\mathcal H}_\Omega}\cdots V_{i,n_i}|_{{\mathcal K}_\Omega}]$ is a pure row isometry;(iii) if
 $i\in \Omega^c$, then
$i\in \Omega^c$, then  $V_i|_{{\mathcal H}_\Omega}:=[V_{i,1}|_{{\mathcal H}_\Omega}\cdots V_{i,n_i}|_{{\mathcal H}_\Omega}]$ is a Cuntz row isometry;
$V_i|_{{\mathcal H}_\Omega}:=[V_{i,1}|_{{\mathcal H}_\Omega}\cdots V_{i,n_i}|_{{\mathcal H}_\Omega}]$ is a Cuntz row isometry;(iv) the subspace
 ${\mathcal H}_\Omega$ is reducing for all the unitary operators in
${\mathcal H}_\Omega$ is reducing for all the unitary operators in  ${\mathcal U}$, and the row isometries
${\mathcal U}$, and the row isometries
 \begin{equation*}V_i|_{{\mathcal H}_\Omega}:=[V_{i,1}|_{{\mathcal H}_\Omega}\cdots V_{i,n_i}|_{{\mathcal H}_\Omega}],\qquad i\in \{1,\ldots, k\},
\end{equation*}
\begin{equation*}V_i|_{{\mathcal H}_\Omega}:=[V_{i,1}|_{{\mathcal H}_\Omega}\cdots V_{i,n_i}|_{{\mathcal H}_\Omega}],\qquad i\in \{1,\ldots, k\},
\end{equation*}are doubly
 ${\mathcal U}|_{{\mathcal H}_\Omega}$-commuting, where
${\mathcal U}|_{{\mathcal H}_\Omega}$-commuting, where  ${\mathcal U}|_{{\mathcal H}_\Omega}:=\{U_{i,j}(s,t)|_{{\mathcal H}_\Omega}\}_{(i,j,s,t)\in \Gamma}$.
${\mathcal U}|_{{\mathcal H}_\Omega}:=\{U_{i,j}(s,t)|_{{\mathcal H}_\Omega}\}_{(i,j,s,t)\in \Gamma}$.
Consequently, we have
 \begin{equation}
\mathrm{curv}(V)=\sum_{\Omega\subset \{1,\ldots, k\}} \mathrm{curv}(V|_{{\mathcal H}_\Omega})\ \text{and } \ \Delta_V(I)=\bigoplus_{\Omega\subset \{1,\ldots, k\}} \Delta_{V|_{{\mathcal H}_\Omega}}(I_{_{{\mathcal H}_\Omega}}).
\end{equation}
\begin{equation}
\mathrm{curv}(V)=\sum_{\Omega\subset \{1,\ldots, k\}} \mathrm{curv}(V|_{{\mathcal H}_\Omega})\ \text{and } \ \Delta_V(I)=\bigoplus_{\Omega\subset \{1,\ldots, k\}} \Delta_{V|_{{\mathcal H}_\Omega}}(I_{_{{\mathcal H}_\Omega}}).
\end{equation} If ![]() $\Omega=\{1,\ldots, k\}$ and
$\Omega=\{1,\ldots, k\}$ and ![]() ${\mathcal H}_{\{1,\ldots, k\}}\neq \{0\}$, then
${\mathcal H}_{\{1,\ldots, k\}}\neq \{0\}$, then  $V|_{{\mathcal H}_{\{1,\ldots, k\}}}$ is a tuple of pure row isometries which, according to theorem 2.4 and theorem 1.6 from from [Reference Popescu27], is unitarily equivalent to the standard
$V|_{{\mathcal H}_{\{1,\ldots, k\}}}$ is a tuple of pure row isometries which, according to theorem 2.4 and theorem 1.6 from from [Reference Popescu27], is unitarily equivalent to the standard  $I\otimes U|_{{\mathcal L}_{\{1,\ldots, k\}}}$-twisted multi-shift S on the Hilbert space
$I\otimes U|_{{\mathcal L}_{\{1,\ldots, k\}}}$-twisted multi-shift S on the Hilbert space  $\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal L}_{\{1,\ldots, k\}}$, where
$\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal L}_{\{1,\ldots, k\}}$, where
 \begin{equation*}
{\mathcal L}_{\{1,\ldots, k\}}:= \bigcap_{{i\in \{1,\ldots, k\}}\atop{s\in \{1,\ldots, n_i\}}} \ker V_{i,s}^*.
\end{equation*}
\begin{equation*}
{\mathcal L}_{\{1,\ldots, k\}}:= \bigcap_{{i\in \{1,\ldots, k\}}\atop{s\in \{1,\ldots, n_i\}}} \ker V_{i,s}^*.
\end{equation*}Hence, we deduce that
 \begin{equation*}
\begin{split}
\mathrm{curv}(V|_{{\mathcal H}_{\{1,\ldots, k\}}})&=\mathrm{rank}\, \Delta_{V|_{{\mathcal H}_{\{1,\ldots, k\}}}}(I_{{\mathcal H}_{\{1,\ldots, k\}}})=\mathrm{curv}(\textbf{S})\\
&=\text{trace} (\textbf{S})
=\mathrm{rank}\,(\Delta_\textbf{S}(I))=\dim\bigcap_{{i\in \{1,\ldots, k\}}\atop{s\in \{1,\ldots, n_i\}}} \ker V_{i,s}^*.
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
\mathrm{curv}(V|_{{\mathcal H}_{\{1,\ldots, k\}}})&=\mathrm{rank}\, \Delta_{V|_{{\mathcal H}_{\{1,\ldots, k\}}}}(I_{{\mathcal H}_{\{1,\ldots, k\}}})=\mathrm{curv}(\textbf{S})\\
&=\text{trace} (\textbf{S})
=\mathrm{rank}\,(\Delta_\textbf{S}(I))=\dim\bigcap_{{i\in \{1,\ldots, k\}}\atop{s\in \{1,\ldots, n_i\}}} \ker V_{i,s}^*.
\end{split}
\end{equation*} On the other hand, if ![]() $\Omega\subset \{1,\ldots, k\}$ and
$\Omega\subset \{1,\ldots, k\}$ and ![]() $\Omega\neq \{1,\ldots, k\}$, then, for any
$\Omega\neq \{1,\ldots, k\}$, then, for any ![]() $i\in \Omega^c$,
$i\in \Omega^c$, ![]() $V_i|_{{\mathcal H}_\Omega}$ is a Cuntz isometry, i.e.
$V_i|_{{\mathcal H}_\Omega}$ is a Cuntz isometry, i.e.  $\sum_{s=1}^{n_i} (V_{i,s}V_{i,s}^*)|_{{\mathcal H}_\Omega}=I_{{\mathcal H}_\Omega}$, which implies
$\sum_{s=1}^{n_i} (V_{i,s}V_{i,s}^*)|_{{\mathcal H}_\Omega}=I_{{\mathcal H}_\Omega}$, which implies ![]() $\mathrm{curv}(V|_{{\mathcal H}_\Omega})=0$ and
$\mathrm{curv}(V|_{{\mathcal H}_\Omega})=0$ and  $\Delta_{V|_{{\mathcal H}_\Omega}}(I_{_{{\mathcal H}_\Omega}})=0$. Using relation (7.1), we deduce that
$\Delta_{V|_{{\mathcal H}_\Omega}}(I_{_{{\mathcal H}_\Omega}})=0$. Using relation (7.1), we deduce that
 \begin{equation*}
\begin{split}
\mathrm{curv}(V)=\mathrm{curv}(V|_{{\mathcal H}_{\{1,\ldots, k\}}})=\dim\bigcap_{{i\in \{1,\ldots, k\}}\atop{s\in \{1,\ldots, n_i\}}} \ker V_{i,s}^*
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
\mathrm{curv}(V)=\mathrm{curv}(V|_{{\mathcal H}_{\{1,\ldots, k\}}})=\dim\bigcap_{{i\in \{1,\ldots, k\}}\atop{s\in \{1,\ldots, n_i\}}} \ker V_{i,s}^*
\end{split}
\end{equation*}and
 \begin{equation*}
\begin{split}
\mathrm{rank}\, \Delta_V(I)=\mathrm{rank}\, \Delta_{V|_{{\mathcal H}_{\{1,\ldots, k\}}}}(I_{{\mathcal H}_{\{1,\ldots, k\}}}).
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
\mathrm{rank}\, \Delta_V(I)=\mathrm{rank}\, \Delta_{V|_{{\mathcal H}_{\{1,\ldots, k\}}}}(I_{{\mathcal H}_{\{1,\ldots, k\}}}).
\end{split}
\end{equation*} This proves items (i) and (ii). We already know that if S is the standard k-tuple of doubly ![]() $I\otimes {\mathcal U}$-commuting row isometries on the Hilbert space
$I\otimes {\mathcal U}$-commuting row isometries on the Hilbert space  $ \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal L}$, where
$ \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal L}$, where ![]() $\dim {\mathcal L} \lt \infty$, then
$\dim {\mathcal L} \lt \infty$, then ![]() $\mathrm{curv}(\textbf{S})=\dim {\mathcal L}$. This proves part (iii).
$\mathrm{curv}(\textbf{S})=\dim {\mathcal L}$. This proves part (iii).
Now, assume that ![]() $m:=\mathrm{curv} (V)\neq 0$. Due to the Wold decomposition mentioned above, we may assume that
$m:=\mathrm{curv} (V)\neq 0$. Due to the Wold decomposition mentioned above, we may assume that  ${\mathcal H}=\left[\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal L}_{\{1,\ldots, k\}}\right]\oplus {\mathcal H}'$ and
${\mathcal H}=\left[\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal L}_{\{1,\ldots, k\}}\right]\oplus {\mathcal H}'$ and ![]() $V=\textbf{S}\oplus V'$, where V ʹ is a doubly
$V=\textbf{S}\oplus V'$, where V ʹ is a doubly ![]() ${\mathcal U}|_{{\mathcal H}'}$-commuting tuple of row isometries with
${\mathcal U}|_{{\mathcal H}'}$-commuting tuple of row isometries with ![]() $\Delta_{V'}(I_{{\mathcal H}'}) =0$ and
$\Delta_{V'}(I_{{\mathcal H}'}) =0$ and  $\textbf{S}=\bigoplus_{p=1}^m \textbf{S}_{\textbf{z}^{(p)}}$, where
$\textbf{S}=\bigoplus_{p=1}^m \textbf{S}_{\textbf{z}^{(p)}}$, where ![]() $m:=\dim {\mathcal L}_{\{1,\ldots, k\}}$. Therefore, we may assume that the multi-shift S is a direct sum of multi-shifts
$m:=\dim {\mathcal L}_{\{1,\ldots, k\}}$. Therefore, we may assume that the multi-shift S is a direct sum of multi-shifts  $\textbf{S}_\textbf{z}\in B(\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+))$ with the scalar weights
$\textbf{S}_\textbf{z}\in B(\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+))$ with the scalar weights ![]() $\textbf{z}=(z_{i,j}(s,t))_{(i,j,s,t)\in \Gamma}$, where
$\textbf{z}=(z_{i,j}(s,t))_{(i,j,s,t)\in \Gamma}$, where ![]() $z_{i,j}(s,t)\in {\mathbb T}$ and
$z_{i,j}(s,t)\in {\mathbb T}$ and  $z_{j,i}(t,s)=\overline{z_{i,j}(s,t})$ for
$z_{j,i}(t,s)=\overline{z_{i,j}(s,t})$ for ![]() $(i,j,s,t)\in \Gamma$.
$(i,j,s,t)\in \Gamma$.
Due to theorem 7.2, for each ![]() $t_p\in (0,1]$,
$t_p\in (0,1]$, ![]() $p\in \{1,\ldots, m\}$, there is an invariant subspace
$p\in \{1,\ldots, m\}$, there is an invariant subspace  ${\mathcal M}_p\subset
\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)$ under
${\mathcal M}_p\subset
\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)$ under ![]() $ \textbf{S}_{\textbf{z}^{(p)}}$ such that
$ \textbf{S}_{\textbf{z}^{(p)}}$ such that  $\mathrm{curv}(P_{{\mathcal M}_p^\perp} \textbf{S}_{\textbf{z}^{(p)}}|_{{\mathcal M}_p^\perp})=t_p$. Note that
$\mathrm{curv}(P_{{\mathcal M}_p^\perp} \textbf{S}_{\textbf{z}^{(p)}}|_{{\mathcal M}_p^\perp})=t_p$. Note that  $(\bigoplus_{p=1}^m {\mathcal M}_p^\perp)\bigoplus {\mathcal H}'$ is invariant under
$(\bigoplus_{p=1}^m {\mathcal M}_p^\perp)\bigoplus {\mathcal H}'$ is invariant under  $\left(\bigoplus_{p=1}^m \textbf{S}^*_{\textbf{z}^{(p)}}\right)\oplus {V'}^*$ and
$\left(\bigoplus_{p=1}^m \textbf{S}^*_{\textbf{z}^{(p)}}\right)\oplus {V'}^*$ and ![]() ${\mathcal U}$. Then
${\mathcal U}$. Then  ${\mathcal M}:=\left((\bigoplus_{p=1}^m {\mathcal M}_p^\perp)\bigoplus {\mathcal H}'\right)^\perp$ is an invariant subspace under
${\mathcal M}:=\left((\bigoplus_{p=1}^m {\mathcal M}_p^\perp)\bigoplus {\mathcal H}'\right)^\perp$ is an invariant subspace under  $V=\left(\bigoplus_{p=1}^m \textbf{S}_{\textbf{z}^{(p)}}\right)\oplus {V'}$ and
$V=\left(\bigoplus_{p=1}^m \textbf{S}_{\textbf{z}^{(p)}}\right)\oplus {V'}$ and ![]() ${\mathcal U}$ and
${\mathcal U}$ and
 \begin{equation*}
\mathrm{curv}(P_{{\mathcal M}^\perp}V|_{{\mathcal M}^\perp})=\sum_{p=1}^m \mathrm{curv}(P_{{\mathcal M}_p^\perp} \textbf{S}_{\textbf{z}^{(p)}}|_{{\mathcal M}_p^\perp}) + \mathrm{curv} (V')=\sum_{p=1}^m t_p.
\end{equation*}
\begin{equation*}
\mathrm{curv}(P_{{\mathcal M}^\perp}V|_{{\mathcal M}^\perp})=\sum_{p=1}^m \mathrm{curv}(P_{{\mathcal M}_p^\perp} \textbf{S}_{\textbf{z}^{(p)}}|_{{\mathcal M}_p^\perp}) + \mathrm{curv} (V')=\sum_{p=1}^m t_p.
\end{equation*} On the other hand, using a similar argument and proposition 7.4, we find a nontrivial invariant subspace ![]() ${\mathcal M}\subset {\mathcal H}$ under V such that
${\mathcal M}\subset {\mathcal H}$ under V such that ![]() $ \mathrm{curv}(P_{{\mathcal M}^\perp}V|_{{\mathcal M}^\perp})=0$. This completes the proof.
$ \mathrm{curv}(P_{{\mathcal M}^\perp}V|_{{\mathcal M}^\perp})=0$. This completes the proof.
We recall the following result which is needed in what follows. If  ${\mathcal M}\subset \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal K}$ is an invariant subspace under the multi-shift
${\mathcal M}\subset \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)\otimes {\mathcal K}$ is an invariant subspace under the multi-shift ![]() $\textbf{S}_{\mathcal U}$ and
$\textbf{S}_{\mathcal U}$ and ![]() $I\otimes {\mathcal U}$, then
$I\otimes {\mathcal U}$, then ![]() $\textbf{S}_{\mathcal U}|_{\mathcal M}$ is in the regular
$\textbf{S}_{\mathcal U}|_{\mathcal M}$ is in the regular ![]() $(I\otimes{\mathcal U})|_{\mathcal M}$-twisted polyball if and only if
$(I\otimes{\mathcal U})|_{\mathcal M}$-twisted polyball if and only if ![]() ${\mathcal M}$ is a Beurling type invariant subspace for
${\mathcal M}$ is a Beurling type invariant subspace for ![]() $\textbf{S}_{\mathcal U}$ and
$\textbf{S}_{\mathcal U}$ and ![]() $I\otimes{\mathcal U}$.
$I\otimes{\mathcal U}$.
Proposition. Let  ${\mathcal M}\subset \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)$ be a proper invariant subspace of the z-twisted multi-shift
${\mathcal M}\subset \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)$ be a proper invariant subspace of the z-twisted multi-shift ![]() $\mathbf{S_z}$. Then
$\mathbf{S_z}$. Then ![]() $\mathbf{S}_\mathbf{z}|_{\mathcal M} $ is in the
$\mathbf{S}_\mathbf{z}|_{\mathcal M} $ is in the ![]() $(I\otimes \mathbf{z})|_{\mathcal M}$-twisted polyball and
$(I\otimes \mathbf{z})|_{\mathcal M}$-twisted polyball and ![]() $\mathrm{curv}(P_{{\mathcal M}^\perp} \textbf{S}_\textbf{z}|_{{\mathcal M}^\perp})=0$ if and only if there is an inner sequence
$\mathrm{curv}(P_{{\mathcal M}^\perp} \textbf{S}_\textbf{z}|_{{\mathcal M}^\perp})=0$ if and only if there is an inner sequence ![]() $\{\Psi_s\}_{s=1}^\infty$ for
$\{\Psi_s\}_{s=1}^\infty$ for ![]() ${\mathcal M}$, i.e.
${\mathcal M}$, i.e. ![]() $\Psi_s$ are isometric multipliers of
$\Psi_s$ are isometric multipliers of  $\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)$ with respect to
$\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)$ with respect to ![]() $\textbf{S}_\textbf{z}$ such that
$\textbf{S}_\textbf{z}$ such that
 \begin{equation*} P_{\mathcal M}=\sum_{s=1}^\infty \Psi_s\Psi_s^*,
\end{equation*}
\begin{equation*} P_{\mathcal M}=\sum_{s=1}^\infty \Psi_s\Psi_s^*,
\end{equation*}where the convergence is in the strong operator topology and
 \begin{equation*}
\lim_{(q_1,\ldots, q_k)\in {\mathbb Z}_+^k} \frac{1}{n_1^{q_1}\cdots n_k^{q_k}}
\sum_{|\alpha_1|=q_1, \ldots, |\alpha_k|=q_k}\sum_{s=1}^\infty \|\Psi_s(\chi_{\alpha_1, \cdots, \alpha_k)}\|^2=1.
\end{equation*}
\begin{equation*}
\lim_{(q_1,\ldots, q_k)\in {\mathbb Z}_+^k} \frac{1}{n_1^{q_1}\cdots n_k^{q_k}}
\sum_{|\alpha_1|=q_1, \ldots, |\alpha_k|=q_k}\sum_{s=1}^\infty \|\Psi_s(\chi_{\alpha_1, \cdots, \alpha_k)}\|^2=1.
\end{equation*}Proof. According to the remarks preceding this proposition, ![]() $\mathbf{S}_\mathbf{z}|_{\mathcal M} $ is in the
$\mathbf{S}_\mathbf{z}|_{\mathcal M} $ is in the ![]() $(I\otimes \mathbf{z})|_{\mathcal M}$-twisted polyball if and only if
$(I\otimes \mathbf{z})|_{\mathcal M}$-twisted polyball if and only if ![]() ${\mathcal M}$ is a Beurling type invariant subspace under
${\mathcal M}$ is a Beurling type invariant subspace under ![]() $\mathbf{S_z}$. Therefore, there exist multi-analytic operators
$\mathbf{S_z}$. Therefore, there exist multi-analytic operators  $\Psi_p\in B( \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)$ such that
$\Psi_p\in B( \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)$ such that ![]() $P_{\mathcal M}=\sum_{s=1}^\infty \Psi_s\Psi_s^*$. Due to theorem 6.1 and corollary 6.2, condition
$P_{\mathcal M}=\sum_{s=1}^\infty \Psi_s\Psi_s^*$. Due to theorem 6.1 and corollary 6.2, condition ![]() $\mathrm{curv}(P_{{\mathcal M}^\perp} \mathbf{S}|_{{\mathcal M}^\perp})=0$ is equivalent to
$\mathrm{curv}(P_{{\mathcal M}^\perp} \mathbf{S}|_{{\mathcal M}^\perp})=0$ is equivalent to
 \begin{equation*}
\begin{split} \lim_{(q_1,\ldots, q_k)\in {\mathbb Z}_+^k}
\frac{\mathrm{trace\,}\left[\left(\sum_{s=1}^\infty \Psi_s\Psi_s^*\right)P_{(q_1,\ldots, q_k)} \right]}{\mathrm{trace\,}\left[P_{(q_1,\ldots, q_k)} \right]}=1.
\end{split}
\end{equation*}
\begin{equation*}
\begin{split} \lim_{(q_1,\ldots, q_k)\in {\mathbb Z}_+^k}
\frac{\mathrm{trace\,}\left[\left(\sum_{s=1}^\infty \Psi_s\Psi_s^*\right)P_{(q_1,\ldots, q_k)} \right]}{\mathrm{trace\,}\left[P_{(q_1,\ldots, q_k)} \right]}=1.
\end{split}
\end{equation*}Now, one can easily complete the proof.
Proposition 7.7. If  ${\mathcal M}\subset \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)$ is a proper Beurling type invariant subspace of multi-shift
${\mathcal M}\subset \ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)$ is a proper Beurling type invariant subspace of multi-shift ![]() $\mathbf{S_z}$, then
$\mathbf{S_z}$, then
Proof. As in the proof of proposition 6.7, there is a unitary operator ![]() $\psi:\overline{{\Delta_{A}}(I)({\mathcal M}^\perp)}\to {\mathbb C}$ such that
$\psi:\overline{{\Delta_{A}}(I)({\mathcal M}^\perp)}\to {\mathbb C}$ such that ![]() $(I\otimes \psi){K_A}=V$, where
$(I\otimes \psi){K_A}=V$, where ![]() ${K_A}$ is the Berezin kernel associated with
${K_A}$ is the Berezin kernel associated with ![]() $A:=P_{{\mathcal M}^\perp} \textbf{S}_\textbf{z}|_{{\mathcal M}^\perp}$ and V is the injection of
$A:=P_{{\mathcal M}^\perp} \textbf{S}_\textbf{z}|_{{\mathcal M}^\perp}$ and V is the injection of ![]() ${\mathcal M}^\perp$ into
${\mathcal M}^\perp$ into  $\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)$. Hence, we deduce that
$\ell^2({\mathbb F}_{n_1}^+\times\cdots \times {\mathbb F}_{n_k}^+)$. Hence, we deduce that ![]() ${K_{A}} {K_{A}^*}=(I\otimes \psi^*)P_{{\mathcal M}^\perp} (I\otimes \psi)$ and
${K_{A}} {K_{A}^*}=(I\otimes \psi^*)P_{{\mathcal M}^\perp} (I\otimes \psi)$ and
Since ![]() ${\mathcal M}$ is a Beurling type invariant subspace, we have
${\mathcal M}$ is a Beurling type invariant subspace, we have ![]() $\Delta_{\textbf{S}_\textbf{z}}(P_{\mathcal M})\geq 0$, which implies
$\Delta_{\textbf{S}_\textbf{z}}(P_{\mathcal M})\geq 0$, which implies ![]() $\Delta_{\textbf{S}_\textbf{z}}(I-{K_{A}}{K_{A}^*})\geq 0$. Now, assume that
$\Delta_{\textbf{S}_\textbf{z}}(I-{K_{A}}{K_{A}^*})\geq 0$. Now, assume that ![]() $\mathrm{curv}({A})=1$. t Then,
$\mathrm{curv}({A})=1$. t Then, ![]() $\mathrm{curv}(A)=\mathrm{rank}\, A$ and, due to corollary 5.5, A is unitarily equivalent to
$\mathrm{curv}(A)=\mathrm{rank}\, A$ and, due to corollary 5.5, A is unitarily equivalent to ![]() $\textbf{S}_\textbf{z}$. Hence, we deduce that
$\textbf{S}_\textbf{z}$. Hence, we deduce that ![]() ${\mathcal M}^\perp$ is an invariant subspace for
${\mathcal M}^\perp$ is an invariant subspace for ![]() $\textbf{S}_\textbf{z}$. This shows that
$\textbf{S}_\textbf{z}$. This shows that ![]() ${\mathcal M}^\perp$ is a reducing subspace for
${\mathcal M}^\perp$ is a reducing subspace for ![]() $\textbf{S}_\textbf{z}$. Since the
$\textbf{S}_\textbf{z}$. Since the ![]() $C^*$-algebra
$C^*$-algebra ![]() $C^*(\textbf{S}_\textbf{z})$ is irreducible (see [Reference Popescu27]), we get a contradiction. This completes the proof.
$C^*(\textbf{S}_\textbf{z})$ is irreducible (see [Reference Popescu27]), we get a contradiction. This completes the proof.
We remark that proposition 7.7 implies that ![]() $P_{{\mathcal M}^\perp} \textbf{S}_\textbf{z}|_{{\mathcal M}^\perp}$ is not unitarily equivalent to
$P_{{\mathcal M}^\perp} \textbf{S}_\textbf{z}|_{{\mathcal M}^\perp}$ is not unitarily equivalent to ![]() $\textbf{S}_\textbf{z}$. It remains an open question whether proposition 7.7 remains true for arbitrary proper invariant subspace of
$\textbf{S}_\textbf{z}$. It remains an open question whether proposition 7.7 remains true for arbitrary proper invariant subspace of ![]() $\textbf{S}_\textbf{z}$, which is the case when k = 1 and
$\textbf{S}_\textbf{z}$, which is the case when k = 1 and ![]() ${\mathcal U}=\{1_{\mathbb C}\}$ (see [Reference Popescu20]).
${\mathcal U}=\{1_{\mathbb C}\}$ (see [Reference Popescu20]).