Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-23T20:27:04.189Z Has data issue: false hasContentIssue false
  • English
  • Français

The number of solutions of the Erdős-Straus Equation and sums of k unit fractions

Part of: Diophantine equations

Published online by Cambridge University Press:  30 January 2019

Christian Elsholtz  and
Stefan Planitzer
Christian Elsholtz
Affiliation:
Graz University of Technology, Institute of Analysis and Number Theory, Kopernikusgasse 24/II, Graz8010, Austria ([email protected]; [email protected])
Stefan Planitzer
Affiliation:
Graz University of Technology, Institute of Analysis and Number Theory, Kopernikusgasse 24/II, Graz8010, Austria ([email protected]; [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove new upper bounds for the number of representations of an arbitrary rational number as a sum of three unit fractions. In particular, for fixed m there are at most 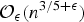${\cal O}_{\epsilon }(n^{{3}/{5}+\epsilon })$ solutions of 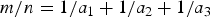${m}/{n} = {1}/{a_1} + {1}/{a_2} + {1}/{a_3}$. This improves upon a result of Browning and Elsholtz (2011) and extends a result of Elsholtz and Tao (2013) who proved this when m=4 and n is a prime. Moreover, there exists an algorithm finding all solutions in expected running time 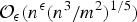${\cal O}_{\epsilon }(n^{\epsilon }({n^3}/{m^2})^{{1}/{5}})$, for any 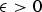$\epsilon \gt 0$. We also improve a bound on the maximum number of representations of a rational number as a sum of k unit fractions. Furthermore, we also improve lower bounds. In particular, we prove that for given 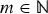$m \in {\open N}$ in every reduced residue class e mod f there exist infinitely many primes p such that the number of solutions of the equation 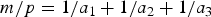${m}/{p} = {1}/{a_1} + {1}/{a_2} + {1}/{a_3}$ is 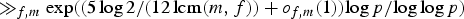$\gg _{f,m} \exp (({5\log 2}/({12\,{\rm lcm} (m,f)}) + o_{f,m}(1)) {\log p}/{\log \log p})$. Previously, the best known lower bound of this type was of order 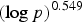$(\log p)^{0.549}$.

Keywords

unit fractionsErdős-Straus equationDiophantine equations

MSC classification

Primary: 11D68: Rational numbers as sums of fractions
Secondary: 11D72: Equations in many variables
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 150 , Issue 3 , June 2020 , pp. 1401 - 1427
Copyright
Copyright © 2019 The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Aigner, A.. Brüche als Summe von Stammbrüchen. J. Reine Angew. Math. 214/215 (1964), 174–179.Google Scholar
2Arce-Nazario, R., Castro, F. and Figueroa, R.. On the number of solutions of $\sum \nolimits _{i=1}^{11} 1/{x_i}=1$ in distinct odd natural numbers. J. Number Theory 133 (2013), 2036–2046.CrossRefGoogle Scholar
3Benjamin, A. T., Chen, B. and Kindred, K.. Sums of evenly spaced binomial coefficients. Math. Mag. 83 (2010), 370–373.CrossRefGoogle Scholar
4Brenton, L. and Hill, R.. On the Diophantine equation $1=\sum 1/n_i+1/\prod n_i$ and a class of homologically trivial complex surface singularities. Pacific J. Math. 133 (1988), 41–67.CrossRefGoogle Scholar
5Browning, T. D. and Elsholtz, C.. The number of representations of rationals as a sum of unit fractions. Illinois J. Math. 55 (2011), 685–696.CrossRefGoogle Scholar
6Chang, M.-C.. Short character sums for composite moduli. J. Anal. Math. 123 (2014), 1–33.CrossRefGoogle Scholar
7Chen, Y.-G., Elsholtz, C. and Jiang, L.-L.. Egyptian fractions with restrictions. Acta Arith. 154 (2012), 109–123.CrossRefGoogle Scholar
8Dedekind, R.. Über Zerlegungen von Zahlen durch ihre größten gemeinsamen Teiler. In Gesammelte mathematische Werke, Zweiter Band (eds. Fricke, R., Noether, E. and Ore, Ö.). pp. 103–147 (Friedr. Vieweg & Sohn Akt.-Ges.: Braunschweig, 1931) Available online at http://resolver.sub.uni-goettingen.de/purl?PPN235693928.Google Scholar
9Elsholtz, C.. Sums of k Unit Fractions, Shaker Verlag, Aachen, 1999, Phd Thesis, Technische Universität Darmstadt (1998), 109 pages.Google Scholar
10Elsholtz, C.. Sums of k unit fractions. Trans. Amer. Math. Soc. 353 (2001), 3209–3227.CrossRefGoogle Scholar
11Elsholtz, C.. Egyptian fractions with odd denominators. Q. J. Math. 67 (2016), 425–430.CrossRefGoogle Scholar
12Elsholtz, C. and Tao, T.. Counting the number of solutions to the Erdős–Straus equation on unit fractions. J. Aust. Math. Soc. 94 (2013), 50–105.CrossRefGoogle Scholar
13Graham, R. L.. On finite sums of reciprocals of distinct nth powers. Pacific J. Math. 14 (1964), 85–92.CrossRefGoogle Scholar
14Graham, R. L.. On finite sums of unit fractions. Proc. London Math. Soc. (3) 14 (1964), 193–207.CrossRefGoogle Scholar
15Graham, R. L.. Paul Erdős and Egyptian fractions. In Erdős Centennial, Bolyai Soc. Math. Stud. (eds.Lovász, L., Ruzsa, I. Z. and Sós, V. T.), vol. 25, pp. 289–309 (Budapest: János Bolyai Math. Soc., 2013).Google Scholar
16Guy, R. K.. Unsolved problems in number theory, 3rd edn (New York: Springer-Verlag, 2010).Google Scholar
17Hall, R. R.. On the distribution of divisors of integers in residue classes (mod k). J. Number Theory 2 (1970), 168–188.CrossRefGoogle Scholar
18Hardy, G. H. and Wright, E. M.. An introduction to the theory of numbers, 6th edn (Oxford: Oxford University Press, 2008).Google Scholar
19Harman, G.. On the number of Carmichael numbers up to x. Bull. London Math. Soc. 37 (2005), 641–650.CrossRefGoogle Scholar
20Harman, G.. Watt's mean value theorem and Carmichael numbers. Int. J. Number Theory 4 (2008), 241–248.CrossRefGoogle Scholar
21Konyagin, S. V.. Double exponential lower bound for the number of representations of unity by Egyptian fractions. Math. Notes 95 (2014), 277–281, Translation of Mat. Zametki 95 (2014), no. 2, 312–316.CrossRefGoogle Scholar
22Lebesgue, V.-A.. Extrait des exercises d'analyse numérique, Nouvelles annales de mathématiques 1re série 8 (1849), 347–353.Google Scholar
23Lenstra, H. W. Jr. and Pomerance, C.. A rigorous time bound for factoring integers. J. Amer. Math. Soc. 5 (1992), 483–516.CrossRefGoogle Scholar
24Martin, G.. Dense Egyptian fractions. Trans. Amer. Math. Soc. 351 (1999), 3641–3657.CrossRefGoogle Scholar
25Mordell, L. J.. Diophantine equations. Pure and applied mathematics, vol. 30 (London and New York: Academic Press, 1969).Google Scholar
26Rosati, L. A.. Sull'equazione diofantea $4/n= 1/x_1+ 1/x_2+1/x_3$. Boll. Un. Mat. Ital. (3) 9 (1954), 59–63.Google Scholar
27Sándor, C.. On the number of solutions of the Diophantine equation $\sum ^n_{i=1} {1}/{x_i}=1$. Period. Math. Hungar. 47 (2003), 215–219.CrossRefGoogle Scholar
28Stewart, B. M.. Theory of numbers, 2nd edn (New York, London: The Macmillan Company, Collier-Macmillan Limited, 1964).Google Scholar
29Tenenbaum, G.. Introduction à la théorie analytique et probabiliste des nombres, 3rd edn (Paris: Éditions Belin, 2008).Google Scholar
30Xylouris, T.. Über die Nullstellen der Dirichletschen L-Funktionen und die kleinste Primzahl in einer arithmetischen Progression, Universität Bonn, PhD thesis (2011).Google Scholar