No CrossRef data available.
Article contents
A note on lower limit of series and potential theory
Published online by Cambridge University Press: 14 November 2011
Synopsis
We are looking for positive sequences (bn) which have the following property: If (an) is a positive sequence such that 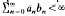 , then
, then
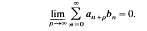
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 121 , Issue 3-4 , 1992 , pp. 273 - 277
- Copyright
- Copyright © Royal Society of Edinburgh 1992
References
1Kaluza, Th.. Uber die Koeffizienten reziproker Potenzreihen. Math. Z. 23 (1928), 000–000.Google Scholar
2Korany, A. and Taylor, J. C.. Fine convergence and parabolic convergence for the Helmoltz equation and heat equation. Illinois J. Math. 27 (1983), 77–93.Google Scholar
3Doob, J. L.. Classical Potential Theory and its Probabilistic Counterpart (Berlin: Springer, 1983).Google Scholar


