Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Thews, Klaus
1981.
T-Periodic solutions of time dependent Hamiltonian systems with a potential vanishing at infinity.
Manuscripta Mathematica,
Vol. 33,
Issue. 3-4,
p.
327.
Kent Nagle, R.
1982.
Nonlinear Phenomena in Mathematical Sciences.
p.
713.
Alfonso, Castro B.
and
Gonçalves, J. V. A.
1982.
Differential Equations.
Vol. 957,
Issue. ,
p.
21.
Bartolo, P.
Benci, V.
and
Fortunato, D.
1983.
Abstract critical point theorems and applications to some nonlinear problems with “strong” resonance at infinity.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 7,
Issue. 9,
p.
981.
Capozzi, A.
Fortunato, D.
and
Salvatore, A.
1985.
Periodic solutions of dynamical systems.
Meccanica,
Vol. 20,
Issue. 4,
p.
281.
Capozzi, A.
and
Salvatore, A.
1985.
Nonlinear problems with strong resonance at infinity: an abstract theorem and applications.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 99,
Issue. 3-4,
p.
333.
Schechter, Martin
1989.
The Hampwile theorem for nonlinear eigenvalues.
Duke Mathematical Journal,
Vol. 59,
Issue. 2,
Schechter, Martin
1990.
Nonlinear elliptic boundary value problems at resonance.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 14,
Issue. 10,
p.
889.
Costa, David G.
and
E Silva, Elves Alves de B.
1991.
The palais-smale condition versus coercivity.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 16,
Issue. 4,
p.
371.
Schechter, Martin
1992.
Differential Equations and Mathematical Physics.
Vol. 186,
Issue. ,
p.
263.
Vakhrameev, S. A.
1993.
Critical point theory for smooth functions on Hilbert manifolds with singularities and its application to some optimal control problems.
Journal of Soviet Mathematics,
Vol. 67,
Issue. 1,
p.
2713.
Schechter, Martin
1993.
Splitting subspaces and saddle points.
Applicable Analysis,
Vol. 49,
Issue. 1-2,
p.
33.
Schechter, Martin
1993.
Generalized Functions and Their Applications.
p.
213.
Schechter, M
1993.
Critical points over splitting subspaces.
Nonlinearity,
Vol. 6,
Issue. 3,
p.
417.
Schechter, Martin
1994.
Asymptotically linear elliptic boundary value problems.
Monatshefte f�r Mathematik,
Vol. 117,
Issue. 1-2,
p.
121.
Rădulescu, Vicenţiu D.
1996.
Nontrivial solutions for a multivalued problem with strong resonance.
Glasgow Mathematical Journal,
Vol. 38,
Issue. 1,
p.
53.
Masiello, Antonio
and
Pisani, Lorenzo
1996.
Asymptotically linear elliptic problems at resonance.
Annali di Matematica Pura ed Applicata,
Vol. 171,
Issue. 1,
p.
1.
Xavier, João Batista de Mendonça
and
Miyagaki, Olimpio Hiroshi
1997.
Remarks on a Resonant Problem withan Unbounded Nonlinearity.
Journal of Mathematical Analysis and Applications,
Vol. 209,
Issue. 1,
p.
255.
Gasiński, Leszek
and
Papageorgiou, Nikolaos S.
1999.
Nonlinear hemivariational inequalities at resonance.
Bulletin of the Australian Mathematical Society,
Vol. 60,
Issue. 3,
p.
353.
Kourogenis, Nikolaos C
and
Papageorgiou, Nikolaos S
1999.
Three Nontrivial Solutions for a Quasilinear Elliptic Differential Equation at Resonance with Discontinuous Right Hand Side.
Journal of Mathematical Analysis and Applications,
Vol. 238,
Issue. 2,
p.
477.
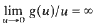 and g satisfies a certain concavity condition at 0 the existence of infinitely many solutions is shown independent of the asymptotic behaviour of g.
and g satisfies a certain concavity condition at 0 the existence of infinitely many solutions is shown independent of the asymptotic behaviour of g.

