Article contents
The non-monotonicity of solutions in swirling flow*
Published online by Cambridge University Press: 14 February 2012
Synopsis
This paper studies the boundary-value problem arising from the behaviour of a fluid occupying the region 0 ≦ x ≧ 1 between two rotating discs, rotating about a common axis perpendicular to their planes, when the discs, are rotating in the same sense with speeds 0 ≦ Ω0<Ω1. The equations which describe the axially symmetric similarity solutions of this problem are

with the boundary conditions
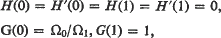
where ε = v/2Ω1 and v is the kinematic viscosity.
The major result is: There is an ε0 such that for 0<ε≦ε0 there does not exist a solution 〈H(x,ε), G(x,ε)〉 with G′(x,ε)≧0.
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 76 , Issue 3 , 1977 , pp. 161 - 182
- Copyright
- Copyright © Royal Society of Edinburgh 1977
References
- 3
- Cited by


