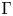1. Introduction
This paper is focussed on the approximation of brittle fracture energies for linearly elastic materials, by means of non-local functionals defined on Sobolev spaces. The asymptotic behaviour of these functionals will simultaneously show the emergence both of effective energies for the elastic deformation (which may be, e.g., the output of homogenization), and of Griffith-type surface energies accounting for crack formation. In turn, this result can be further generalized to the setting of stochastic homogenization with fracture.
Precisely our results will extend the range of application of the recent papers [Reference Farroni, Scilla and Solombrino17, Reference Scilla and Solombrino22] while also providing some relevant technical improvement. We briefly comment on these previous contributions, in order to introduce our results. There, an approach originally devised by Braides and Dal Maso [Reference Dal Maso and Braides13] for the approximation of the Mumford-Shah functional has been generalized to the linearly elastic setting. Namely, it was shown that, for a given bounded increasing function $f\colon \mathbb {R}^+\to \mathbb {R}^+$![]() the energies
the energies
$\Gamma$![]() -converge, in the $L^1(U)$
-converge, in the $L^1(U)$![]() -topology, to the functional
-topology, to the functional
with $\alpha =f^\prime (0)$![]() and $\beta =\lim _{t\to +\infty }f(t)$
and $\beta =\lim _{t\to +\infty }f(t)$![]() . Above, $\rho _k$
. Above, $\rho _k$![]() are rescaled convolution kernels with unit mass and compact convex symmetrical support $S$
are rescaled convolution kernels with unit mass and compact convex symmetrical support $S$![]() , $\phi _\rho$
, $\phi _\rho$![]() is (twice) the support function of $S$
is (twice) the support function of $S$![]() [see (2.4) for its precise definition], $W(e(u))$
[see (2.4) for its precise definition], $W(e(u))$![]() is a convex elastic energy with superlinear $p$
is a convex elastic energy with superlinear $p$![]() growth depending on the symmetrized gradient $e(u)$
growth depending on the symmetrized gradient $e(u)$![]() of a vector-valued displacement $u$
of a vector-valued displacement $u$![]() , whose jump set is denoted by $J_u$
, whose jump set is denoted by $J_u$![]() . Notice that the effective domains of the approximations and of the limit are different. Actually (1.1) is finite on the Sobolev space $W^{1,p}(U;\mathbb {R}^n)$
. Notice that the effective domains of the approximations and of the limit are different. Actually (1.1) is finite on the Sobolev space $W^{1,p}(U;\mathbb {R}^n)$![]() , while the energy space of (1.2) is the one of generalized functions with bounded deformation $GSBD^p(U)$
, while the energy space of (1.2) is the one of generalized functions with bounded deformation $GSBD^p(U)$![]() , introduced in [Reference Dal Maso11].
, introduced in [Reference Dal Maso11].
We stress that the above results allowed one for a general (convex) bulk energy. The proof strategy cannot rely, at least when estimating the bulk part, on any slicing procedure. The latter is instead successful in the particular case $W(\xi )=|\xi |^p$![]() , considered for instance in [Reference Negri20]. We also remark that the results of [Reference Farroni, Scilla and Solombrino17, Reference Scilla and Solombrino22] were obtained under an additional structural assumption on the kernels $\rho _k$
, considered for instance in [Reference Negri20]. We also remark that the results of [Reference Farroni, Scilla and Solombrino17, Reference Scilla and Solombrino22] were obtained under an additional structural assumption on the kernels $\rho _k$![]() , which have to be radial with respect to the norm induced by $S$
, which have to be radial with respect to the norm induced by $S$![]() . In the particular case considered in [Reference Negri20], this restriction was instead not needed.
. In the particular case considered in [Reference Negri20], this restriction was instead not needed.
A natural extension of the aforementioned models allows one to include an explicit dependence on $k$![]() and on the space variable of the energy density. This amounts to consider functionals of the form
and on the space variable of the energy density. This amounts to consider functionals of the form
whose limit behaviour is the object of the present paper. Functionals of the form (1.3) can be used to approximate (1.2) with some gain in the ease of minimization, for a proper choice of $W_k$![]() . Actually, this more general setting is also suitable for further applications, if one thinks about the mechanical counterpart of the model. Indeed energy densities of type $W_k(y,M)$
. Actually, this more general setting is also suitable for further applications, if one thinks about the mechanical counterpart of the model. Indeed energy densities of type $W_k(y,M)$![]() , where $y$
, where $y$![]() is the position in the reference configuration, are customary when dealing with heterogeneous material with some microstructures. The prototypical example is the case of homogenisation, that is, when $W_k(y,M)=W\left (\frac {y}{\delta _k},M\right )$
is the position in the reference configuration, are customary when dealing with heterogeneous material with some microstructures. The prototypical example is the case of homogenisation, that is, when $W_k(y,M)=W\left (\frac {y}{\delta _k},M\right )$![]() with $\delta _k\searrow 0$
with $\delta _k\searrow 0$![]() . Taking this point of view amounts to regard (1.3) as a nonlocal linearly elastic model, with a truncated potential $\frac 1{\varepsilon _k}f(\varepsilon _k \cdot )$
. Taking this point of view amounts to regard (1.3) as a nonlocal linearly elastic model, with a truncated potential $\frac 1{\varepsilon _k}f(\varepsilon _k \cdot )$![]() accounting for the cost of breaking the elastic bonds on regions of size $\varepsilon _k$
accounting for the cost of breaking the elastic bonds on regions of size $\varepsilon _k$![]() . In such a case, one is interested in deriving an effective asymptotic model for (1.3).
. In such a case, one is interested in deriving an effective asymptotic model for (1.3).
The main result of our paper is contained in theorem 2.1. There we show that the functionals in (1.3) $\Gamma$![]() -converge to a limit energy of the form
-converge to a limit energy of the form
Above, the limit bulk density $W$![]() can be characterised in terms of cell formula [see (2.7)–(2.8)]. Remarkably, that coincides exactly with the asymptotic formula that one would obtain by considering the limit behaviour of the local energies $\int _UW_k(x,e(u))\,{\rm d}x$
can be characterised in terms of cell formula [see (2.7)–(2.8)]. Remarkably, that coincides exactly with the asymptotic formula that one would obtain by considering the limit behaviour of the local energies $\int _UW_k(x,e(u))\,{\rm d}x$![]() in the Sobolev space $W^{1,p}(U)$
in the Sobolev space $W^{1,p}(U)$![]() . Hence, a decoupling effect between bulk and surface contribution occurs, since the volume energy only depends on $f$
. Hence, a decoupling effect between bulk and surface contribution occurs, since the volume energy only depends on $f$![]() through its derivative at the origin. A similar effect has been observed in [Reference Cortesani9] where the analogue of (1.3) for energies depending on the full deformation gradient was taken into account. On the one hand, the possibility of using smooth truncations (a tool which is not available in $GSBD$
through its derivative at the origin. A similar effect has been observed in [Reference Cortesani9] where the analogue of (1.3) for energies depending on the full deformation gradient was taken into account. On the one hand, the possibility of using smooth truncations (a tool which is not available in $GSBD$![]() ) allowed the author there to replace $f$
) allowed the author there to replace $f$![]() by a sequence $f_k$
by a sequence $f_k$![]() and to derive more general surface energies in the limit. On the other hand, the precise characterisation of the volume energy density was obtained at the expense of an additional technical condition on the $W_k$
and to derive more general surface energies in the limit. On the other hand, the precise characterisation of the volume energy density was obtained at the expense of an additional technical condition on the $W_k$![]() 's (the so-called stable $\gamma$
's (the so-called stable $\gamma$![]() -convergence). It actually turns out, as an output of our proof strategy, that this extra assumption can be dropped (see Appendix). Thus, our results also permit some improvement in the previous literature about non-local approximation of free-discontinuity problems.
-convergence). It actually turns out, as an output of our proof strategy, that this extra assumption can be dropped (see Appendix). Thus, our results also permit some improvement in the previous literature about non-local approximation of free-discontinuity problems.
We now come to the description of our proof technique. The most difficult point is the lower bound for the bulk contribution. This is done in proposition 5.1, by means of a localisation and blow-up procedure which contains some elements of novelty in the non-local setting. More precisely, we consider the blow-up of sequences with equi-bounded energies at a Lebesgue point for the limit energy. A crucial task is to gain a uniform control on the $L^p$![]() norm of the symmetrized gradients of the blow-up functions up to sets with vanishing perimeter. This allows us to apply [Reference Friedrich, Perugini and Solombrino18, lemma 5.1] (which relies on the Korn-type inequality of [Reference Cagnetti, Chambolle and Scardia6]): we can substitute, with almost no change in the energy, the above mentioned sequence with a more regular one bounded in $W^{1,p}$
norm of the symmetrized gradients of the blow-up functions up to sets with vanishing perimeter. This allows us to apply [Reference Friedrich, Perugini and Solombrino18, lemma 5.1] (which relies on the Korn-type inequality of [Reference Cagnetti, Chambolle and Scardia6]): we can substitute, with almost no change in the energy, the above mentioned sequence with a more regular one bounded in $W^{1,p}$![]() . Exploiting the properties of $f$
. Exploiting the properties of $f$![]() , we are then reconducted to analyse the limit behaviour on small squares of a local energy in $W^{1,p}$
, we are then reconducted to analyse the limit behaviour on small squares of a local energy in $W^{1,p}$![]() , which can be estimated from below via a cell formula.
, which can be estimated from below via a cell formula.
An optimal estimate from below for the surface term can be obtained by means of a slicing procedure (proposition 5.3). As for the $\Gamma$![]() -limsup inequality it can be achieved by a direct construction for a class of competitors with regular jump set, which are dense in energy. Here, we use the classical approximation result of[Reference Chambolle and Crismale7, Reference Cortesani and Toader10].
-limsup inequality it can be achieved by a direct construction for a class of competitors with regular jump set, which are dense in energy. Here, we use the classical approximation result of[Reference Chambolle and Crismale7, Reference Cortesani and Toader10].
We underline that even in the case of (1.1) (i.e., with $W$![]() not depending on $k$
not depending on $k$![]() ) we have some technical improvement in comparison with the result of [Reference Farroni, Scilla and Solombrino17, Reference Scilla and Solombrino22]. First of all, we do not need anymore to assume the kernels $\rho _k$
) we have some technical improvement in comparison with the result of [Reference Farroni, Scilla and Solombrino17, Reference Scilla and Solombrino22]. First of all, we do not need anymore to assume the kernels $\rho _k$![]() to be radially symmetric. Secondly, our $\Gamma$
to be radially symmetric. Secondly, our $\Gamma$![]() -convergence argument is carried out with respect to the convergence in measure instead of the $L^1$
-convergence argument is carried out with respect to the convergence in measure instead of the $L^1$![]() convergence. This is (almost) the natural one for sequences with equibounded energy (see theorem 2.1-$(ii)$
convergence. This is (almost) the natural one for sequences with equibounded energy (see theorem 2.1-$(ii)$![]() ). It can be indeed shown that such sequences are compact in the measure convergence up to an exceptional set $U^\infty$
). It can be indeed shown that such sequences are compact in the measure convergence up to an exceptional set $U^\infty$![]() , where their modulus diverges. However, this set can be easily made empty by adding a penalisation term in the energy (see the statement of theorem 3.5 and remark 2.2).
, where their modulus diverges. However, this set can be easily made empty by adding a penalisation term in the energy (see the statement of theorem 3.5 and remark 2.2).
Eventually, we complement our analysis with a stochastic homogenisation result theorem 7.4. Namely, we consider functionals of type (1.3) with stationary random integrands
where $\omega$![]() belongs to the sample space $\Omega$
belongs to the sample space $\Omega$![]() of a probability space $(\Omega,\mathcal {T},P)$
of a probability space $(\Omega,\mathcal {T},P)$![]() and $\delta _k\searrow 0$
and $\delta _k\searrow 0$![]() . Following the approach proposed by [Reference Dal Maso and Modica12] (which relies on the Subadditive Ergodic Theorem in [Reference Krengel and Akcoglu19]) we show that, almost surely, such functionals $\Gamma$
. Following the approach proposed by [Reference Dal Maso and Modica12] (which relies on the Subadditive Ergodic Theorem in [Reference Krengel and Akcoglu19]) we show that, almost surely, such functionals $\Gamma$![]() -converge to a free-discontinuity functional of the form (1.4) where the bulk energy density is independent of the space variable. A similar result was obtained in [Reference Bach, Marziani and Zeppieri2] in the context of elliptic approximation of free-discontinuity functionals.
-converge to a free-discontinuity functional of the form (1.4) where the bulk energy density is independent of the space variable. A similar result was obtained in [Reference Bach, Marziani and Zeppieri2] in the context of elliptic approximation of free-discontinuity functionals.
Plan of the paper. The paper is structured as follows. After fixing the notation, in § 2, we introduce the problem, discuss the assumptions and state our main results. § 3 is devoted to recalling preliminary results which are useful for the analysis. The proof of theorem 2.1 is carried out through the § 4–6, dealing with compactness, lower, and upper bound, respectively. In § 7, we prove a stochastic homogenisation result theorem 7.4. Eventually in the Appendix, we briefly comment on the result of [Reference Cortesani9, theorem 3.2], highlighting that the assumptions made there can actually be weakened. A complete statement is given for the readers’ convenience in theorem A.1.
2. Setting of the problem and main results
2.1 Notation
We start by collecting the notation adopted throughout the paper.
(a) $n\geq 2$
 is a fixed integer and $p>1$
is a fixed integer and $p>1$ is a fixed real number;
is a fixed real number;(b) $\mathbb {M}^{n\times n}$
 denotes the space of $n\times n$
denotes the space of $n\times n$ real matrices; $\mathbb {M}^{n\times n}_{\rm sym}$
real matrices; $\mathbb {M}^{n\times n}_{\rm sym}$ and $\mathbb {M}^{n\times n}_{\rm skew}$
and $\mathbb {M}^{n\times n}_{\rm skew}$ denote the spaces of symmetric and skew-symmetric matrices respectively;
denote the spaces of symmetric and skew-symmetric matrices respectively;(c) for a subset $A\subset \mathbb {R}^n$
 $\partial ^*A$
$\partial ^*A$ denotes the essential boundary of $A$
denotes the essential boundary of $A$ ;
;(d) $\mathcal {L}^n$
 and and $\mathcal {H}^{n-1}$
and and $\mathcal {H}^{n-1}$ denote the Lebesgue measure and the $(n-1)$
denote the Lebesgue measure and the $(n-1)$ -dimensional Hausdorff measure on $\mathbb {R}^n$
-dimensional Hausdorff measure on $\mathbb {R}^n$ , respectively;
, respectively;(e) for every $A\subset \mathbb {R}^n$
 let $\chi _A$
let $\chi _A$ denote the characteristic function of the set $A$
denote the characteristic function of the set $A$ ;
;(f) $U$
 denotes an open bounded subset of $\mathbb {R}^n$
denotes an open bounded subset of $\mathbb {R}^n$ with Lipschitz boundary;
with Lipschitz boundary;(g) we denote by $\mathcal {A}(U)$
 and $\mathcal {A}$
and $\mathcal {A}$ the collection of all open and bounded subsets of $U$
the collection of all open and bounded subsets of $U$ and $\mathbb {R}^n$
and $\mathbb {R}^n$ respectively;
respectively;(h) If $A,B \in \mathcal {A}(U)$
 (or $\mathcal {A}$
(or $\mathcal {A}$ ) by $A \subset \subset B$
) by $A \subset \subset B$ we mean that $A$
we mean that $A$ is relatively compact in $B$
is relatively compact in $B$ ;
;(i) $Q$
 and $Q'$
and $Q'$ denote the open unit cube in $\mathbb {R}^n$
denote the open unit cube in $\mathbb {R}^n$ and $\mathbb {R}^{n-1}$
and $\mathbb {R}^{n-1}$ respectively with sides parallel to the coordinate axis, centred at the origin; for $x\in \mathbb {R}^n$
respectively with sides parallel to the coordinate axis, centred at the origin; for $x\in \mathbb {R}^n$ (respectively $x\in \mathbb {R}^{n-1}$
(respectively $x\in \mathbb {R}^{n-1}$ ) and $r>0$
) and $r>0$ , we set $Q_r(x):= rQ+x$
, we set $Q_r(x):= rQ+x$ (respectively ${Q'_r(x):= rQ'+x}$
(respectively ${Q'_r(x):= rQ'+x}$ );
);(j) for every $\xi \in {\mathbb {S}}^{n-1}$
 let $R_\xi$
let $R_\xi$ denote an orthogonal $(n\times n)$
denote an orthogonal $(n\times n)$ -matrix such that $R_\xi e_n=\xi$
-matrix such that $R_\xi e_n=\xi$ ;
;(k) for $x\in \mathbb {R}^n$
 , $r>0$
, $r>0$ , and $\xi \in \mathbb {S}^{n-1}$
, and $\xi \in \mathbb {S}^{n-1}$ , we define $Q^\xi _r(x):=R_\xi Q_r(x)$
, we define $Q^\xi _r(x):=R_\xi Q_r(x)$ .
.(l) for a given topological space $X$
 , $\mathcal {B}(X)$
, $\mathcal {B}(X)$ denotes the Borel $\sigma$
denotes the Borel $\sigma$ - algebra on $X$
- algebra on $X$ . If $X=\mathbb {R}^d$
. If $X=\mathbb {R}^d$ , with $d\in \mathbb {N}$
, with $d\in \mathbb {N}$ , $d\ge 1$
, $d\ge 1$ we simply write $\mathcal {B}^d$
we simply write $\mathcal {B}^d$ in place of $\mathcal {B}(\mathbb {R}^d)$
in place of $\mathcal {B}(\mathbb {R}^d)$ . For $d=1$
. For $d=1$ we write $\mathcal {B}$
we write $\mathcal {B}$ ;
;(m) we denote by $L^0(U;\mathbb {R}^n)$
 the space of measurable functions;
the space of measurable functions;(n) for $a,b\in \mathbb {R}^n$
 the symbol $a \otimes b$
the symbol $a \otimes b$ denotes the tensor product between $a$
denotes the tensor product between $a$ and $b$
and $b$ , while $a\odot b:=\frac 12 (a\otimes b+b\otimes a)$
, while $a\odot b:=\frac 12 (a\otimes b+b\otimes a)$ .
.
Throughout the paper, $C$![]() denotes a strictly positive constant which may vary from line to line and within the same expression.
denotes a strictly positive constant which may vary from line to line and within the same expression.
2.2 (G)SBV and (G)SBD functions
We will work with the functional spaces $(G)SBV^p(U;\mathbb {R}^n)$![]() and $(G)SBD^p(U)$
and $(G)SBD^p(U)$![]() for which we will recall the main properties and refer the reader to [Reference Ambrosio, Fusco and Pallara1, Reference Dal Maso11] for a complete exposition of the subject. We say that $u\in L^1(U;\mathbb {R}^n)$
for which we will recall the main properties and refer the reader to [Reference Ambrosio, Fusco and Pallara1, Reference Dal Maso11] for a complete exposition of the subject. We say that $u\in L^1(U;\mathbb {R}^n)$![]() belongs to the space of special functions with bounded variation, i.e., $u\in SBV(U;\mathbb {R}^n)$
belongs to the space of special functions with bounded variation, i.e., $u\in SBV(U;\mathbb {R}^n)$![]() , if its distributional gradient is a finite $\mathbb {M}^{n\times n}$
, if its distributional gradient is a finite $\mathbb {M}^{n\times n}$![]() -valued Radon measure without Cantor part, that is,
-valued Radon measure without Cantor part, that is,
where $\nabla u$![]() is the approximate gradient, $J_u$
is the approximate gradient, $J_u$![]() is the approximate jump set, $[u]=u^+-u^-$
is the approximate jump set, $[u]=u^+-u^-$![]() the jump opening and $\nu _u$
the jump opening and $\nu _u$![]() the unit normal to $J_u$
the unit normal to $J_u$![]() . A function $u\in L^0(U;\mathbb {R}^n)$
. A function $u\in L^0(U;\mathbb {R}^n)$![]() belongs to the space of generalised special functions with bounded variation, i.e., $u\in GSBV(U;\mathbb {R}^n)$
belongs to the space of generalised special functions with bounded variation, i.e., $u\in GSBV(U;\mathbb {R}^n)$![]() , if for any $\varphi \in C^1(\mathbb {R}^n;\mathbb {R}^n)$
, if for any $\varphi \in C^1(\mathbb {R}^n;\mathbb {R}^n)$![]() with support of $\nabla \varphi$
with support of $\nabla \varphi$![]() compact it holds $\varphi \circ u\in SBV_{\rm loc}(U;\mathbb {R}^n)$
compact it holds $\varphi \circ u\in SBV_{\rm loc}(U;\mathbb {R}^n)$![]() .
.
We say that $u\in L^1(U;\mathbb {R}^n)$![]() belongs to the space of special functions with bounded deformation, and we write $u\in SBD(U)$
belongs to the space of special functions with bounded deformation, and we write $u\in SBD(U)$![]() , if its symmetrized distributional gradient is a finite $\mathbb {M}^{n\times n}_{\rm sym}$
, if its symmetrized distributional gradient is a finite $\mathbb {M}^{n\times n}_{\rm sym}$![]() -valued Radon measure without Cantor part, that is,
-valued Radon measure without Cantor part, that is,
where $e(u)$![]() is the approximate symmetric gradient with respect to the Lebesgue measure. On the contrary, the space of generalised special functions with bounded deformation, $GSBD(U)$
is the approximate symmetric gradient with respect to the Lebesgue measure. On the contrary, the space of generalised special functions with bounded deformation, $GSBD(U)$![]() , cannot be defined analogously to the space $GSBV(U;\mathbb {R}^n)$
, cannot be defined analogously to the space $GSBV(U;\mathbb {R}^n)$![]() as if $u\in SBD(U)$
as if $u\in SBD(U)$![]() and $\varphi$
and $\varphi$![]() is as above, then in general $\varphi \circ u\notin SBD(U)$
is as above, then in general $\varphi \circ u\notin SBD(U)$![]() . To overcome this issue, Dal Maso in [Reference Dal Maso11] proposed a definition of this space by relying on a slicing argument which we describe in the following.
. To overcome this issue, Dal Maso in [Reference Dal Maso11] proposed a definition of this space by relying on a slicing argument which we describe in the following.
For $\xi \in \mathbb {R}^n\setminus \{0\}$![]() we let $\Pi ^\xi := \{y\in \mathbb {R}^n\colon \langle \xi,y\rangle =0\}$
we let $\Pi ^\xi := \{y\in \mathbb {R}^n\colon \langle \xi,y\rangle =0\}$![]() ; for any $y\in \Pi ^\xi$
; for any $y\in \Pi ^\xi$![]() and $A\in \mathcal {B}(U)$
and $A\in \mathcal {B}(U)$![]() , we set
, we set
Given $u\colon U\to \mathbb {R}^n$![]() we define $u^{\xi,y}\colon U_{\xi,y}\to \mathbb {R}$
we define $u^{\xi,y}\colon U_{\xi,y}\to \mathbb {R}$![]() by
by
If $u^{\xi,y}\in SBV(U_{\xi,y};\mathbb {R})$![]() , we set
, we set
We then say that $u\in L^0(U;\mathbb {R}^n)$![]() belongs to the space of generalised special functions with bounded deformation, and we write $u\in GSBD(U)$
belongs to the space of generalised special functions with bounded deformation, and we write $u\in GSBD(U)$![]() , if there exists a bounded Radon measure $\lambda$
, if there exists a bounded Radon measure $\lambda$![]() on $U$
on $U$![]() such that $u^{\xi,y}\in SBV_{\rm loc}(U_{\xi,y})$
such that $u^{\xi,y}\in SBV_{\rm loc}(U_{\xi,y})$![]() for all $\nu \in \mathbb {S}^{n-1}$
for all $\nu \in \mathbb {S}^{n-1}$![]() and all $y\in \Pi ^\xi$
and all $y\in \Pi ^\xi$![]() and
and
for all $A\in \mathcal {B}(U)$![]() . Eventually, we set
. Eventually, we set

and
where $\nabla u$![]() and $e(u)$
and $e(u)$![]() are well defined also in $GSBV(U;\mathbb {R}^n)$
are well defined also in $GSBV(U;\mathbb {R}^n)$![]() and $GSBD(U)$
and $GSBD(U)$![]() respectively.
respectively.
2.3 Setting of the problem
Let $1< p<+\infty$![]() ; let $c_1,c_2$
; let $c_1,c_2$![]() be given positive constants such that $0< c_1\le c_2<+\infty$
be given positive constants such that $0< c_1\le c_2<+\infty$![]() . Let $\mathcal {W}:= \mathcal {W}(p,c_1,c_2)$
. Let $\mathcal {W}:= \mathcal {W}(p,c_1,c_2)$![]() be the collection of all functions $W\colon \mathbb {R}^n\times \mathbb {M}^{n\times n}\to \mathbb {R}$
be the collection of all functions $W\colon \mathbb {R}^n\times \mathbb {M}^{n\times n}\to \mathbb {R}$![]() satisfying the following conditions:
satisfying the following conditions:
(W1) $W$
 is a Carathéodory function on $\mathbb {R}^n\times \mathbb {M}^{n\times n}$
is a Carathéodory function on $\mathbb {R}^n\times \mathbb {M}^{n\times n}$ ;
;(W2) ($W2$
 ) $W(x,0)=0$
) $W(x,0)=0$ for every $x\in \mathbb {R}^n$
for every $x\in \mathbb {R}^n$ ;
;(W3) for every $x\in \mathbb {R}^n$
 , $M\in \mathbb {M}^{n\times n}$
, $M\in \mathbb {M}^{n\times n}$ and $S\in \mathbb {M}^{n\times n}_{\rm skew}$
and $S\in \mathbb {M}^{n\times n}_{\rm skew}$ \[ W(x,M+S)=W(x,M)\,; \]
\[ W(x,M+S)=W(x,M)\,; \]
(W4) for every $x\in \mathbb {R}^n$
 and every $M\in \mathbb {M}^{n\times n}$
and every $M\in \mathbb {M}^{n\times n}$ \[ c_1|M+M^T|^p\le W(x,M)\le c_2(|M+M^T|^p+1)\,. \]
\[ c_1|M+M^T|^p\le W(x,M)\le c_2(|M+M^T|^p+1)\,. \]
Let $f\colon [0,+\infty )\to [0,+\infty )$![]() be a concaveFootnote 1 increasing function such that there exist $\alpha,\beta >0$
be a concaveFootnote 1 increasing function such that there exist $\alpha,\beta >0$![]() with
with
Note that for such $f$![]() it holds
it holds
moreover by [Reference Scilla and Solombrino22, lemma 2.10] there exist $(\alpha _i)_{i\in \mathbb {N}}$![]() , $(\beta _i)_{i\in \mathbb {N}}$
, $(\beta _i)_{i\in \mathbb {N}}$![]() sequences of positive numbers with $\sup _i\alpha _i=\alpha$
sequences of positive numbers with $\sup _i\alpha _i=\alpha$![]() , $\sup _i\beta _i=\beta$
, $\sup _i\beta _i=\beta$![]() such that
such that
Let $\rho \in L^\infty (\mathbb {R}^n;[0,+\infty ))$![]() be a lower semi-continuous convolution kernel with $\int _{\mathbb {R}^n}\rho \,{\rm d}x=1$
be a lower semi-continuous convolution kernel with $\int _{\mathbb {R}^n}\rho \,{\rm d}x=1$![]() and $S:= {\{\rho >0\}}$
and $S:= {\{\rho >0\}}$![]() bounded, convex, symmetrical and with $0\in S$
bounded, convex, symmetrical and with $0\in S$![]() . We denote by $|\cdot |_S$
. We denote by $|\cdot |_S$![]() the norm induced by $S$
the norm induced by $S$![]() , namely,
, namely,
Under the above assumptions, $|\cdot |_S$![]() is a norm and $S=\{|x|_S<1\}$
is a norm and $S=\{|x|_S<1\}$![]() . Then for any bounded set $K\subset \mathbb {R}^n$
. Then for any bounded set $K\subset \mathbb {R}^n$![]() and $x\in \mathbb {R}^n$
and $x\in \mathbb {R}^n$![]() , we let
, we let
For any Borel set $E$![]() and any $r>0$
and any $r>0$![]() , we denote by $E_r$
, we denote by $E_r$![]() and $E_{-r}$
and $E_{-r}$![]() respectively the sets
respectively the sets
Finally, we let $\phi _\rho \colon \mathbb {R}^n\to [0,+\infty )$![]() be given by
be given by
For $\delta >0$![]() , we set $\rho _\delta (x):= \frac 1{\delta ^n}\rho \left (\frac x{\delta }\right )$
, we set $\rho _\delta (x):= \frac 1{\delta ^n}\rho \left (\frac x{\delta }\right )$![]() , $S_\delta (x):= x+\delta S$
, $S_\delta (x):= x+\delta S$![]() .
.
For $k\in \mathbb {N}$![]() let $(W_k)\subset \mathcal {W}$
let $(W_k)\subset \mathcal {W}$![]() , let $(\varepsilon _k)$
, let $(\varepsilon _k)$![]() be a decreasing sequence of strictly positive real numbers converging to zero, as $k\to +\infty$
be a decreasing sequence of strictly positive real numbers converging to zero, as $k\to +\infty$![]() and let $\rho _k:= \rho _{\varepsilon _k}$
and let $\rho _k:= \rho _{\varepsilon _k}$![]() . We consider the family of functionals $F_k\colon L^0(U;\mathbb {R}^n)\to [0,+\infty ]$
. We consider the family of functionals $F_k\colon L^0(U;\mathbb {R}^n)\to [0,+\infty ]$![]() defined as
defined as

Here and henceforth, it remains understood that each $u\in W^{1,p}(U;\mathbb {R}^n)$![]() is extended to a fixed neighbourhood of $U$
is extended to a fixed neighbourhood of $U$![]() to have a well-defined functional. The $\Gamma$
to have a well-defined functional. The $\Gamma$![]() -limit, as we will see, is independent of the considered extension. Let $x\in \mathbb {R}^n$
-limit, as we will see, is independent of the considered extension. Let $x\in \mathbb {R}^n$![]() , $M\in \mathbb {M}^{n\times n}$
, $M\in \mathbb {M}^{n\times n}$![]() , $A\in \mathcal {A}$
, $A\in \mathcal {A}$![]() and $u\in W^{1,p}(A;\mathbb {R}^n)$
and $u\in W^{1,p}(A;\mathbb {R}^n)$![]() be fixed. Set $u_M(y):= My$
be fixed. Set $u_M(y):= My$![]() . We then define the minimisation problem
. We then define the minimisation problem
and the cell formulas
Notice that $W'$![]() and $W''$
and $W''$![]() depend on the given sequence of $k$
depend on the given sequence of $k$![]() and are to be modified accordingly if one takes subsequences. This will be highlighted in the statement of our main result.
and are to be modified accordingly if one takes subsequences. This will be highlighted in the statement of our main result.
2.4 Main results
In this Section we state our main results. The first one is a $\Gamma$![]() -convergence theorem for the energies $F_k$
-convergence theorem for the energies $F_k$![]() .
.
Theorem 2.1 $\Gamma$![]() -convergence of $F_k$
-convergence of $F_k$![]()
Let $F_k$![]() be as in (2.5). Then the following hold:
be as in (2.5). Then the following hold:
(i) There exists a subsequence, not relabelled, such that for every $x\in U$
 and every $M\in \mathbb {M}^{n\times n}$
and every $M\in \mathbb {M}^{n\times n}$ , and for $W'$
, and for $W'$ , $W''$
, $W''$ as in (2.7) and (2.8) (calculated for the given subsequence), one has
(2.9)\begin{equation} W'(x,M)=W''(x,M):=W(x, M)\,. \end{equation}and it holds $W(x,M)=W(x,{\rm sym}(M))$
as in (2.7) and (2.8) (calculated for the given subsequence), one has
(2.9)\begin{equation} W'(x,M)=W''(x,M):=W(x, M)\,. \end{equation}and it holds $W(x,M)=W(x,{\rm sym}(M))$
 . Moreover, $F_k$
. Moreover, $F_k$ $\Gamma$
$\Gamma$ -converges with respect to the convergence in measure to the functional $F\colon L^0(U;\mathbb {R}^n) \to [0,+\infty ]$
-converges with respect to the convergence in measure to the functional $F\colon L^0(U;\mathbb {R}^n) \to [0,+\infty ]$ given by
(2.10)\begin{equation} F(u):=\begin{cases} \displaystyle\ \alpha\int_UW(x,e(u))\,{\rm d}x+\beta \int_{J_u}\phi_\rho(\nu_u)\,{\rm d}\mathcal{H}^{n-1} & \text{if }u\in GSBD^p(U)\,,\\ + \infty & \text{otherwise}\,, \end{cases} \end{equation}with $\phi _\rho$
given by
(2.10)\begin{equation} F(u):=\begin{cases} \displaystyle\ \alpha\int_UW(x,e(u))\,{\rm d}x+\beta \int_{J_u}\phi_\rho(\nu_u)\,{\rm d}\mathcal{H}^{n-1} & \text{if }u\in GSBD^p(U)\,,\\ + \infty & \text{otherwise}\,, \end{cases} \end{equation}with $\phi _\rho$
 as in (2.4);
as in (2.4);(ii) Let $(u_k)\subset L^0(U;\mathbb {R}^n)$
 be such that $\sup _kF_k(u_k)<+\infty$
be such that $\sup _kF_k(u_k)<+\infty$ . Set $U^\infty := ~\{x\in U\colon |u_k(x)|\to +\infty \}$
. Set $U^\infty := ~\{x\in U\colon |u_k(x)|\to +\infty \}$ . Then there exists $u\in GSBD^p(U)$
. Then there exists $u\in GSBD^p(U)$ such that, up to subsequence, it holds $u_k\to u$
such that, up to subsequence, it holds $u_k\to u$ in measure on $U\setminus U^\infty$
in measure on $U\setminus U^\infty$ . If in addition
\[ \sup_{k\in\mathbb{N}}\int_U\psi(|u_k|)\,{\rm d}x<{+}\infty\,, \]for some $\psi \colon [0,+\infty )\to [0,+\infty )$
. If in addition
\[ \sup_{k\in\mathbb{N}}\int_U\psi(|u_k|)\,{\rm d}x<{+}\infty\,, \]for some $\psi \colon [0,+\infty )\to [0,+\infty )$
 , continuous, increasing with $\lim _{s\to +\infty }\psi (s)=+\infty$
, continuous, increasing with $\lim _{s\to +\infty }\psi (s)=+\infty$ , then $U^\infty =\emptyset$
, then $U^\infty =\emptyset$ , so that $|u|$
, so that $|u|$ is finite a.e., and $u_k\to u$
is finite a.e., and $u_k\to u$ in measure on $U$
in measure on $U$ .
.
Remark 2.2 The addition of a penalty term of the form $\int _U\psi (|u|)\,{\rm d}x$![]() to the energy enforces then compactness in measure, while causing no troubles in the $\Gamma$
to the energy enforces then compactness in measure, while causing no troubles in the $\Gamma$![]() -convergence analysis. Indeed, such a term is clearly lower semicontinuous, hence the corresponding lower bound follows immediately. As for the upper bound, if one takes $\psi$
-convergence analysis. Indeed, such a term is clearly lower semicontinuous, hence the corresponding lower bound follows immediately. As for the upper bound, if one takes $\psi$![]() as in theorem 3.4, the argument of proposition 6.1 can be readily adapted also in presence of such an additional term. As this is not the core of the argument, we will neglect lower order terms in our statements and proofs, directly assuming that convergence in measure holds everywhere. The technical details left to prove the upper bound are summarized in remark 6.2 for the readers convenience.
as in theorem 3.4, the argument of proposition 6.1 can be readily adapted also in presence of such an additional term. As this is not the core of the argument, we will neglect lower order terms in our statements and proofs, directly assuming that convergence in measure holds everywhere. The technical details left to prove the upper bound are summarized in remark 6.2 for the readers convenience.
The proof of theorem 2.1 is divided into three main steps contained respectively in § 4, 5 and 6. As a consequence of theorem 2.1 and the Urysohn property of $\Gamma$![]() -convergence [Reference Dal Maso14, proposition 8.3], we deduce the following corollary.
-convergence [Reference Dal Maso14, proposition 8.3], we deduce the following corollary.
Corollary 2.3 Let $(W_k)\subset \mathcal {W}$![]() and let $F_k$
and let $F_k$![]() be the functionals as in (2.5). Let $W'$
be the functionals as in (2.5). Let $W'$![]() , $W''$
, $W''$![]() be as in (2.7) and (2.8), respectively. Assume that
be as in (2.7) and (2.8), respectively. Assume that
for some Borel function $W\colon \mathbb {R}^n\times \mathbb {M}^{n\times n}\to [0,+\infty )$![]() . Let $F$
. Let $F$![]() defined as in (2.10) accordingly. Then the functionals $F_k$
defined as in (2.10) accordingly. Then the functionals $F_k$![]() $\Gamma$
$\Gamma$![]() -converge with respect to the convergence in measure to $F$
-converge with respect to the convergence in measure to $F$![]() . Moreover
. Moreover
for every $x\in U$![]() and every $M\in \mathbb {M}^{n\times n}$
and every $M\in \mathbb {M}^{n\times n}$![]() .
.
We now state a homogenisation theorem without assuming any spatial periodicity of the energy densities $W_k$![]() . We start by introducing some notation. We fix $W\in \mathcal {W}$
. We start by introducing some notation. We fix $W\in \mathcal {W}$![]() and set
and set
for all $A\in \mathcal {A}$![]() and all $M\in \mathbb {M}^{n\times n}$
and all $M\in \mathbb {M}^{n\times n}$![]() . Let also $(W_k)\subset \mathcal {W}$
. Let also $(W_k)\subset \mathcal {W}$![]() be given by
be given by
with $\delta _k\searrow 0$![]() when $k\to +\infty$
when $k\to +\infty$![]() .
.
Theorem 2.4 Deterministic homogenisation
Let $W\in \mathcal {W}$![]() and let $\mathbf {m}(u_M,Q_t(tx))$
and let $\mathbf {m}(u_M,Q_t(tx))$![]() be as in (2.11) with $A=Q_t(tx)$
be as in (2.11) with $A=Q_t(tx)$![]() . Assume that for every $x\in \mathbb {R}^n$
. Assume that for every $x\in \mathbb {R}^n$![]() , $M\in \mathbb {M}^{n\times n}$
, $M\in \mathbb {M}^{n\times n}$![]() the following limit
the following limit
exists and is independent of $x$![]() . Then the functionals $F_k$
. Then the functionals $F_k$![]() defined in (2.5) with $W_k$
defined in (2.5) with $W_k$![]() as in (2.12) $\Gamma$
as in (2.12) $\Gamma$![]() -converge with respect to the convergence in measure to the functional $F_{\rm hom}\colon L^0(U;\mathbb {R}^n)\to [0,+\infty ]$
-converge with respect to the convergence in measure to the functional $F_{\rm hom}\colon L^0(U;\mathbb {R}^n)\to [0,+\infty ]$![]() given by
given by

with $\phi _\rho$![]() as in (2.4). Moreover $W_{\rm hom}(M)=W_{\rm hom}({\rm sym}(M))$
as in (2.4). Moreover $W_{\rm hom}(M)=W_{\rm hom}({\rm sym}(M))$![]() for all $M\in \mathbb {M}^{n\times n}$
for all $M\in \mathbb {M}^{n\times n}$![]() .
.
Proof. Let $W'$![]() , $W''$
, $W''$![]() be respectively as in (2.7) and (2.8). By corollary 2.3, it is sufficient to show that
be respectively as in (2.7) and (2.8). By corollary 2.3, it is sufficient to show that
for all $x\in \mathbb {R}^n$![]() and $M\in \mathbb {M}^{n\times n}$
and $M\in \mathbb {M}^{n\times n}$![]() . We fix $x\in \mathbb {R}^n$
. We fix $x\in \mathbb {R}^n$![]() , $M\in \mathbb {M}^{n\times n}$
, $M\in \mathbb {M}^{n\times n}$![]() , $r>0$
, $r>0$![]() and $k\in \mathbb {N}$
and $k\in \mathbb {N}$![]() . For any $u\in W^{1,p}(Q_r(x);\mathbb {R}^n)$
. For any $u\in W^{1,p}(Q_r(x);\mathbb {R}^n)$![]() with $u=u_M$
with $u=u_M$![]() near $\partial Q_r(x)$
near $\partial Q_r(x)$![]() , we let $u_k\in W^{1,p}\left (Q_{\frac r{\delta _k}}\left (\frac x{\delta _k}\right );\mathbb {R}^n\right )$
, we let $u_k\in W^{1,p}\left (Q_{\frac r{\delta _k}}\left (\frac x{\delta _k}\right );\mathbb {R}^n\right )$![]() be given by $u_k(y):= \frac 1{\delta _k}u(\delta _ky)$
be given by $u_k(y):= \frac 1{\delta _k}u(\delta _ky)$![]() . Then clearly $u_k=u_M$
. Then clearly $u_k=u_M$![]() near $\partial Q_{\frac r{\delta _k}}\left (\frac x{\delta _k}\right )$
near $\partial Q_{\frac r{\delta _k}}\left (\frac x{\delta _k}\right )$![]() . Moreover by performing the change of variable $\hat y=\frac y{\delta _k}$
. Moreover by performing the change of variable $\hat y=\frac y{\delta _k}$![]() , we find
, we find

Hence in particular
with $t_k:= \frac r{\delta _k}$![]() . Eventually passing to the limit as $k\to +\infty$
. Eventually passing to the limit as $k\to +\infty$![]() by (2.13), we deduce
by (2.13), we deduce
3. Some preliminary results
In this section, we collect some useful results that will be employed throughout the paper. We start by recalling a $\Gamma$![]() -convergence result for the bulk energies defined in (3.1) (theorem 3.1) and a $\Gamma$
-convergence result for the bulk energies defined in (3.1) (theorem 3.1) and a $\Gamma$![]() -convergence result for one-dimensional non-local energies (theorem 3.3). To follow we recall a density and a compactness result (cf., theorems 3.4 and 3.5). We conclude this section with a series of technical lemmas (cf. lemmas 3.6, 3.7, 3.8 and corollary 3.9).
-convergence result for one-dimensional non-local energies (theorem 3.3). To follow we recall a density and a compactness result (cf., theorems 3.4 and 3.5). We conclude this section with a series of technical lemmas (cf. lemmas 3.6, 3.7, 3.8 and corollary 3.9).
We consider the family of functionals $E_k\colon L^0(\mathbb {R}^n;\mathbb {R}^n)\times \mathcal {A}\to [0,+\infty ]$![]() given by
given by

Theorem 3.1 $\Gamma$![]() -convergence of $E_k$
-convergence of $E_k$![]()
Let $E_k$![]() be as in (3.1). Then there exists a subsequence, not relabelled, such that for every $A\in \mathcal {A}$
be as in (3.1). Then there exists a subsequence, not relabelled, such that for every $A\in \mathcal {A}$![]() the functionals $E_k(\cdot,A)$
the functionals $E_k(\cdot,A)$![]() $\Gamma$
$\Gamma$![]() -converge, with respect to the convergence in measure, to the functional $E(\cdot,A)$
-converge, with respect to the convergence in measure, to the functional $E(\cdot,A)$![]() with $E\colon L^0(\mathbb {R}^n;\mathbb {R}^n)\times \mathcal {A}\to [0,+\infty ]$
with $E\colon L^0(\mathbb {R}^n;\mathbb {R}^n)\times \mathcal {A}\to [0,+\infty ]$![]() given by
given by

where for every $x\in \mathbb {R}^n$![]() and every $M\in \mathbb {M}^{n\times n}$
and every $M\in \mathbb {M}^{n\times n}$![]()
with $W'$![]() , $W''$
, $W''$![]() as in (2.7) and (2.8) for the given subsequence. The same $\Gamma$
as in (2.7) and (2.8) for the given subsequence. The same $\Gamma$![]() -convergence holds with respect to the $L^p_{\rm loc}(\mathbb {R}^n;\mathbb {R}^n)$
-convergence holds with respect to the $L^p_{\rm loc}(\mathbb {R}^n;\mathbb {R}^n)$![]() convergence.
convergence.
Observe that the above theorem yields in particular a subsequence for which (2.9) holds. From now on, it remains understood that such a subsequence has been fixed, without relabelling. The proof of theorem (3.1) is rather standard and follows by the localisation method (see e.g., [Reference Dal Maso14, Sections 18,19]) and by suitably adapting the integral representation result in [Reference Bouchittè, Fonseca, Leoni and Mascarenhas3, theorem 2] to our setting with the help of Korn-Poincaré inequality. For this reason we omit the proof here and we refer the reader to [Reference Friedrich, Perugini and Solombrino18, proposition 3.13] for more details. We only highlight that the result holds also for non regular open bounded subsets of $\mathbb {R}^n$![]() . Since this may not be immediately clear from the statement given in [Reference Friedrich, Perugini and Solombrino18, proposition 3.13], we discuss this point in the remark below.
. Since this may not be immediately clear from the statement given in [Reference Friedrich, Perugini and Solombrino18, proposition 3.13], we discuss this point in the remark below.
Remark 3.2 Let $A$![]() be any open bounded subset of $\mathbb {R}^n$
be any open bounded subset of $\mathbb {R}^n$![]() and $u\in W^{1,p}(A ;\mathbb {R}^n)$
and $u\in W^{1,p}(A ;\mathbb {R}^n)$![]() . We show that there exists a sequence $(u_k)\subset W^{1,p}(A;\mathbb {R}^n)$
. We show that there exists a sequence $(u_k)\subset W^{1,p}(A;\mathbb {R}^n)$![]() such that $u_k\to u$
such that $u_k\to u$![]() in $L^p(A;\mathbb {R}^n)$
in $L^p(A;\mathbb {R}^n)$![]() and $E_k(u_k,A)\to E(u,A)$
and $E_k(u_k,A)\to E(u,A)$![]() . With the use of Korn-Poincaré inequality, it is clear that this can be done if $A$
. With the use of Korn-Poincaré inequality, it is clear that this can be done if $A$![]() is an extension domain. In the general case, consider smooth relatively compact subsets $A'\subset \subset A''\subset \subset A$
is an extension domain. In the general case, consider smooth relatively compact subsets $A'\subset \subset A''\subset \subset A$![]() , and fix $\eta >0$
, and fix $\eta >0$![]() . We find a sequence $(v_k)\subset W^{1,p}(A'';\mathbb {R}^n)$
. We find a sequence $(v_k)\subset W^{1,p}(A'';\mathbb {R}^n)$![]() such that $E_k(v_k,A'')\to E(u,A'')$
such that $E_k(v_k,A'')\to E(u,A'')$![]() . By the liminf inequality, this also gives $E_k(v_k,A''\setminus A')\to E(u,A''\setminus A')$
. By the liminf inequality, this also gives $E_k(v_k,A''\setminus A')\to E(u,A''\setminus A')$![]() . With ($W4$
. With ($W4$![]() ) we have
) we have
Then, considering a cut-off $\varphi$![]() between $A'$
between $A'$![]() and $A''$
and $A''$![]() , we set $u_k:= \varphi v_k+(1-\varphi )u$
, we set $u_k:= \varphi v_k+(1-\varphi )u$![]() . Clearly $u_k\to u$
. Clearly $u_k\to u$![]() in $L^p(A;\mathbb {R}^n)$
in $L^p(A;\mathbb {R}^n)$![]() . Furthermore, by ($W4$
. Furthermore, by ($W4$![]() ) one has
) one has

provided $\mathcal {L}^n(A\setminus A')$![]() is sufficiently small. The limsup inequality, which is the only relevant one, follows by a diagonal argument.
is sufficiently small. The limsup inequality, which is the only relevant one, follows by a diagonal argument.
We recall now the following one-dimensional result for non-local energies given in [Reference Braides4, theorem 3.30].
Theorem 3.3 $\Gamma$![]() -convergence in 1d
-convergence in 1d
Let $I\subset \mathbb {R}$![]() be a bounded interval. Let $f\colon [0,+\infty )\mapsto [0,+\infty )$
be a bounded interval. Let $f\colon [0,+\infty )\mapsto [0,+\infty )$![]() be a lower semi-continuous function satisfying (2.1) for some $\alpha,\beta >0$
be a lower semi-continuous function satisfying (2.1) for some $\alpha,\beta >0$![]() . Consider the family of functionals $G_k\colon L^0(I)\to [0,+\infty ]$
. Consider the family of functionals $G_k\colon L^0(I)\to [0,+\infty ]$![]() defined by
defined by
if $u\in W^{1,p}(I)$![]() and $+\infty$
and $+\infty$![]() otherwise. Then $G_k$
otherwise. Then $G_k$![]() $\Gamma$
$\Gamma$![]() -converge with respect to the convergence in measure, to the functional $G\colon L^0(I)\to [0,+\infty ]$
-converge with respect to the convergence in measure, to the functional $G\colon L^0(I)\to [0,+\infty ]$![]() given by
given by
if $w\in SBV(I)$![]() and $+\infty$
and $+\infty$![]() otherwise.
otherwise.
We next recall an approximation result [Reference Chambolle and Crismale7, theorem 1.1] and a compactness result in $GSBD^p$![]() in [Reference Chambolle and Crismale8] (which generalises [Reference Dal Maso11, theorem 11.3]). To this aim we denote by $\mathcal {W}^\infty _{\rm pw}(U;\mathbb {R}^{n})\subset GSBD^p(U)$
in [Reference Chambolle and Crismale8] (which generalises [Reference Dal Maso11, theorem 11.3]). To this aim we denote by $\mathcal {W}^\infty _{\rm pw}(U;\mathbb {R}^{n})\subset GSBD^p(U)$![]() the space of ‘piecewise smooth’ $SBV$
the space of ‘piecewise smooth’ $SBV$![]() -functions, that is,
-functions, that is,

Theorem 3.4 Density in $GSBD^p$![]()
Let $\phi$![]() be a norm on $\mathbb {R}^n$
be a norm on $\mathbb {R}^n$![]() . Let $u\in GSBD^p(U)$
. Let $u\in GSBD^p(U)$![]() . Then there exists a sequence $(u_j)\subset \mathcal {W}^\infty _{\rm pw}(U;\mathbb {R}^n)$
. Then there exists a sequence $(u_j)\subset \mathcal {W}^\infty _{\rm pw}(U;\mathbb {R}^n)$![]() such that
such that
(i) $u_j\to u\ \text {in measure on }U$
 ;
;(ii) $e(u_j)\to e(u)\ \text {in } L^p(U;\mathbb {M}^{n\times n}_{\rm sym})$
 ;
;(iii) $\lim _{j\to \infty } \int _{J_{u_j}}\phi (\nu _{u_j})\,{\rm d}\mathcal {H}^{n-1}= \int _{J_{u}}\phi (\nu _{u})\,{\rm d}\mathcal {H}^{n-1}$
 .
.
Moreover, if
for some $\psi \colon [0,+\infty )\to [0,+\infty )$![]() , continuous, increasing with
, continuous, increasing with
then
We notice that the approximating class considered above fulfils the additional requirement of having a jump set compactly contained in $U$![]() . This is possible, as shown in [Reference De Philippis, Fusco and Pratelli15, theorem C].
. This is possible, as shown in [Reference De Philippis, Fusco and Pratelli15, theorem C].
Theorem 3.5 Compactness in $GSBD^p$![]()
Let $(u_j)\subset GSBD^p(U)$![]() be a sequence satisfying
be a sequence satisfying
Then there exist a subsequence, still denoted by $(u_j)$![]() , and $u\in GSBD^p(U)$
, and $u\in GSBD^p(U)$![]() with the following properties:
with the following properties:
(i) the set $U^\infty := \{x\in U\colon |u_j|\to +\infty \}$
 has finite perimeter;
has finite perimeter;(ii) $u_j\to u$
 in measure on $U\setminus U^\infty$
in measure on $U\setminus U^\infty$ and $u=0$
and $u=0$ on $U^\infty$
on $U^\infty$ ;
;(iii) $e(u_j)\rightharpoonup e(u)$
 in $L^p(U\setminus U^\infty ;\mathbb {M}^{n\times n}_{\rm sym})$
in $L^p(U\setminus U^\infty ;\mathbb {M}^{n\times n}_{\rm sym})$ ;
;(iv) $\displaystyle \liminf _{j\to +\infty }\mathcal {H}^{n-1}(J_{u_j})\!\ge\! \mathcal {H}^{n-1}(J_u\cap (U\setminus U^\infty ))+\mathcal {H}^{n-1}(U\cap \partial ^*U^\infty )\!\ge\! \mathcal {H}^{n-1} (J_u\cup (U\cap \partial ^*U^\infty ))$
 .
.
In the statement above, the last semicontinuity property is stated in a stronger form than in the original paper, but is also proved there (see [Reference Chambolle and Crismale8, Formula (3.25)]). In the rest of this section we give some technical Lemmas.
Lemma 3.6 Let $g_j\colon \mathbb {R}^n\to [0,+\infty )$![]() be a sequence of equi-integrable functions. Let $E_j\subset \mathbb {R}^n$
be a sequence of equi-integrable functions. Let $E_j\subset \mathbb {R}^n$![]() be such that $\mathcal {L}^n(E_j)\to 0$
be such that $\mathcal {L}^n(E_j)\to 0$![]() and let $\delta _j\searrow 0$
and let $\delta _j\searrow 0$![]() as $j\to +\infty$
as $j\to +\infty$![]() . Then $(g_j\chi _{E_j})*\rho _{\delta _j}\to 0$
. Then $(g_j\chi _{E_j})*\rho _{\delta _j}\to 0$![]() strongly in $L^1(\mathbb {R}^n)$
strongly in $L^1(\mathbb {R}^n)$![]() .
.
Proof. By properties of convolution it holds that
By equi-integrability we have that for every $\varepsilon >0$![]() there is $J\in \mathbb {N}$
there is $J\in \mathbb {N}$![]() such that for every $j\ge J$
such that for every $j\ge J$![]()
from which the thesis follows.
Lemma 3.7 Let $A'$![]() be an open bounded subset of $\mathbb {R}^n$
be an open bounded subset of $\mathbb {R}^n$![]() . Let $g_j\colon A'\to [0,+\infty )$
. Let $g_j\colon A'\to [0,+\infty )$![]() be a sequence of equi-integrable functions. Let $\delta _j\searrow 0$
be a sequence of equi-integrable functions. Let $\delta _j\searrow 0$![]() as $j\to +\infty$
as $j\to +\infty$![]() . Then for every $A\subset \subset A'$
. Then for every $A\subset \subset A'$![]() there holds
there holds
Proof. We consider the sequence of positive measures $\nu _j:= g_j*\rho _{\delta _j}\mathcal {L}^n{\unicode{x221F}} A$![]() . Since $A'$
. Since $A'$![]() is bounded $g_j$
is bounded $g_j$![]() turn out to be equi-bounded in $L^1(A')$
turn out to be equi-bounded in $L^1(A')$![]() , hence we get
, hence we get
Therefore there exist a positive measure $\nu \in \mathcal {M}_b(A)$![]() , a function $g\in L^1(A')$
, a function $g\in L^1(A')$![]() , and a not-relabelled subsequence such that $\nu _j\stackrel {*}{\rightharpoonup }\nu$
, and a not-relabelled subsequence such that $\nu _j\stackrel {*}{\rightharpoonup }\nu$![]() weakly $*$
weakly $*$![]() in $\mathcal {M}_b(A)$
in $\mathcal {M}_b(A)$![]() and $g_j\to g$
and $g_j\to g$![]() weakly in $L^1(A')$
weakly in $L^1(A')$![]() . It remains to show that $\nu =g\mathcal {L}^n{\unicode{x221F}} A$
. It remains to show that $\nu =g\mathcal {L}^n{\unicode{x221F}} A$![]() , indeed this would imply
, indeed this would imply
and we could conclude. Let $\varphi \in C^\infty _c(A)$![]() and let $A\subset \subset A''\subset \subset A'$
and let $A\subset \subset A''\subset \subset A'$![]() be fixed. By Fubini's theorem we have
be fixed. By Fubini's theorem we have

where $\hat \rho _{\delta _j}(x):= \rho _{\delta _j}(-x)$![]() and the last equality follows since $g_j\rightharpoonup g$
and the last equality follows since $g_j\rightharpoonup g$![]() weakly in $L^1(A')$
weakly in $L^1(A')$![]() and $\varphi *\hat \rho _{\delta _j}(x)\to \varphi$
and $\varphi *\hat \rho _{\delta _j}(x)\to \varphi$![]() strongly in $L^\infty (A')$
strongly in $L^\infty (A')$![]() . Thus, we deduce $\nu =g\mathcal {L}^n {\unicode{x221F}} A$
. Thus, we deduce $\nu =g\mathcal {L}^n {\unicode{x221F}} A$![]() and the proof is concluded.
and the proof is concluded.
Lemma 3.8 Let $A\subset \mathbb {R}^{n-1}$![]() . Let $(u_k)\subset L^1(A)$
. Let $(u_k)\subset L^1(A)$![]() be a sequence converging to $u$
be a sequence converging to $u$![]() in $L^1(A)$
in $L^1(A)$![]() . Let $A'\subset \subset A$
. Let $A'\subset \subset A$![]() and let $w_k\colon A'\times Q'\to \mathbb {R}$
and let $w_k\colon A'\times Q'\to \mathbb {R}$![]() be given by $w_k(x,y):= u_k(x+\varepsilon _k y)$
be given by $w_k(x,y):= u_k(x+\varepsilon _k y)$![]() . Then $w_k$
. Then $w_k$![]() converges to $u$
converges to $u$![]() in $L^1(A'\times Q')$
in $L^1(A'\times Q')$![]() .
.
Proof. By Frechet-Kolmogoroff's Theorem, for every $\eta >0$![]() there is $h\in \mathbb {N}$
there is $h\in \mathbb {N}$![]() such that for all $k\ge h$
such that for all $k\ge h$![]() and $y\in Q'$
and $y\in Q'$![]() there holds
there holds
This together with Fubini's theorem yield
for all $k\ge h$![]() . Eventually by letting $\eta \to 0$
. Eventually by letting $\eta \to 0$![]() , we conclude.
, we conclude.
Corollary 3.9 Let $A\subset \mathbb {R}^{n-1}$![]() . Let $(u_k)\subset L^0(A)$
. Let $(u_k)\subset L^0(A)$![]() be a sequence converging to $u$
be a sequence converging to $u$![]() in measure. Let $A'\subset \subset A$
in measure. Let $A'\subset \subset A$![]() and let $w_k\colon A'\times Q'\to \mathbb {R}$
and let $w_k\colon A'\times Q'\to \mathbb {R}$![]() be given by $w_k(x,y):= u_k (x+\varepsilon _k y)$
be given by $w_k(x,y):= u_k (x+\varepsilon _k y)$![]() . Then $w_k$
. Then $w_k$![]() converges to $u$
converges to $u$![]() in measure.
in measure.
Proof. Since ${\rm arctan}(u_k)$![]() converges to ${\rm arctan}(u)$
converges to ${\rm arctan}(u)$![]() in $L^1(A)$
in $L^1(A)$![]() by lemma 3.8 we have that ${\rm arctan}(w_k)$
by lemma 3.8 we have that ${\rm arctan}(w_k)$![]() converges to ${\rm arctan}(u)$
converges to ${\rm arctan}(u)$![]() in $L^1(A'\times Q')$
in $L^1(A'\times Q')$![]() . Hence $w_k$
. Hence $w_k$![]() converges to $u$
converges to $u$![]() in measure.
in measure.
4. Compactness
In this section, we prove point $(ii)$![]() of theorem 2.1.
of theorem 2.1.
Proposition 4.1 Compactness
Let $F_k$![]() be as in (2.5). Let $(u_k)\subset L^0(U;\mathbb {R}^n)$
be as in (2.5). Let $(u_k)\subset L^0(U;\mathbb {R}^n)$![]() be such that $\sup _kF_k(u_k)<+\infty$
be such that $\sup _kF_k(u_k)<+\infty$![]() . Then there exist $\bar {u}_k \in GSBV^p(U; \mathbb {R}^n)$
. Then there exist $\bar {u}_k \in GSBV^p(U; \mathbb {R}^n)$![]() and $u\in GSBD^p(U)$
and $u\in GSBD^p(U)$![]() such that $\bar {u}_k-u_k \to 0$
such that $\bar {u}_k-u_k \to 0$![]() in measure on $U$
in measure on $U$![]() and, up to a subsequence, it holds
and, up to a subsequence, it holds
where $U^\infty := \{x\in U\colon |u_k(x)|\to +\infty \}$![]() . If in addition
. If in addition
for some $\psi \colon [0,+\infty )\to [0,+\infty )$![]() , continuous, increasing with $\lim _{s\to +\infty }\psi (s)=+\infty$
, continuous, increasing with $\lim _{s\to +\infty }\psi (s)=+\infty$![]() , then $U^\infty =\emptyset$
, then $U^\infty =\emptyset$![]() , and all implications hold on $U$
, and all implications hold on $U$![]() .
.
Proof. The proof is inspired by that of [Reference Scilla and Solombrino22, proposition 4.1]. Let $(u_k)$![]() be as in the statement and let $U'\subset \subset U$
be as in the statement and let $U'\subset \subset U$![]() be fixed. We will prove the following claim: there exist ($\bar u_k)\subset GSBV^p(U;\mathbb {R}^n)$
be fixed. We will prove the following claim: there exist ($\bar u_k)\subset GSBV^p(U;\mathbb {R}^n)$![]() and $c_0>0$
and $c_0>0$![]() (independent of $k$
(independent of $k$![]() ) such that
) such that
Now, if (4.2) holds, we fix a sequence $U_i\nearrow U$![]() and apply theorem 3.5 to each $U_i$
and apply theorem 3.5 to each $U_i$![]() . With a diagonal argument we deduce the existence of $u\in GSBD(U)$
. With a diagonal argument we deduce the existence of $u\in GSBD(U)$![]() with $u=0$
with $u=0$![]() on $U^\infty$
on $U^\infty$![]() such that, up to a subsequence,
such that, up to a subsequence,
We remark that since the constant $c_0$![]() is independent of $k$
is independent of $k$![]() , we indeed have $u\in GSBD(U)$
, we indeed have $u\in GSBD(U)$![]() by the very same argument of [Reference Chambolle and Crismale8, Formula (3.33)], with the minor difference that the Radon measure $\lambda$
by the very same argument of [Reference Chambolle and Crismale8, Formula (3.33)], with the minor difference that the Radon measure $\lambda$![]() in the definition of $GSBD$
in the definition of $GSBD$![]() is first defined as local weak$^*$
is first defined as local weak$^*$![]() -limit, but turns eventually out to be uniformly bounded by (4.2). We also get $e(u)\in L^p(U)$
-limit, but turns eventually out to be uniformly bounded by (4.2). We also get $e(u)\in L^p(U)$![]() , since $c_0$
, since $c_0$![]() is independent of $k$
is independent of $k$![]() . Concerning the remaining inequality, for fixed $i$
. Concerning the remaining inequality, for fixed $i$![]() we set $U_i^\infty : =U^\infty \cap U_i$
we set $U_i^\infty : =U^\infty \cap U_i$![]() , then by theorem 3.5 $(iv)$
, then by theorem 3.5 $(iv)$![]() we have
we have

Observing that $U_j^\infty \nearrow U^\infty$![]() by lower semicontinuity of the relative perimeter we have
by lower semicontinuity of the relative perimeter we have
Letting $i \to +\infty$![]() , by monotonicity we get
, by monotonicity we get
and being $\mathcal {H}^{n-1}(U_i\cap \partial ^*U_i^\infty )=\mathcal {H}^{n-1}(U_i\cap \partial ^*U_j^\infty )$![]() for all $j\ge i$
for all $j\ge i$![]() it holds
it holds
Eventually, combining (4.3) with (4.4) and (4.5)

This also gives $u\in GSBD^p(U)$![]() . As the remaining part of the statement follows directly from Chebycheff inequality and Fatou's lemma, we are only left to prove the claim.
. As the remaining part of the statement follows directly from Chebycheff inequality and Fatou's lemma, we are only left to prove the claim.
For fixed $i\in \mathbb {N}$![]() let $f_i(t)=\alpha _i t\wedge \beta _i$
let $f_i(t)=\alpha _i t\wedge \beta _i$![]() be as in (2.3). Choose $\eta \in (0,1)$
be as in (2.3). Choose $\eta \in (0,1)$![]() such that $Q_\eta (0)\subset \subset S$
such that $Q_\eta (0)\subset \subset S$![]() and let
and let
Then we have

We set

Note that

Indeed if $x\in A_k^2$![]() there is $z\in A_k^1$
there is $z\in A_k^1$![]() with $Q_{\eta \varepsilon _{k}}(z)\subset Q_{\varepsilon _{k}}(x)$
with $Q_{\eta \varepsilon _{k}}(z)\subset Q_{\varepsilon _{k}}(x)$![]() and therefore
and therefore
By combining together (4.7) and (4.8) we find
By the coarea formula (see e.g., [Reference Evans and Gariepy16, theorem 3.14]) and the mean value theorem there exists $t_k\in (0,(1-\eta )\varepsilon _{k})$![]() such that the set $A_k^3:= \{\operatorname {dist}(\cdot,A_k^1)\le t_k \}\subset A_k^2$
such that the set $A_k^3:= \{\operatorname {dist}(\cdot,A_k^1)\le t_k \}\subset A_k^2$![]() satisfies
satisfies
Let now

By construction $\bar u_k\in GSBV^p(U;\mathbb {R}^n)$![]() . By (4.9) and the fact that $A_k^3\subset A_k^2$
. By (4.9) and the fact that $A_k^3\subset A_k^2$![]() we have $\mathcal {L}^n(A_k^3)\to 0$
we have $\mathcal {L}^n(A_k^3)\to 0$![]() as $k\to +\infty$
as $k\to +\infty$![]() from which (4.1) follows. On the other hand as $J_{\bar u_k}\subseteq \partial A_k^3$
from which (4.1) follows. On the other hand as $J_{\bar u_k}\subseteq \partial A_k^3$![]() (4.9) and (4.10) yield
(4.9) and (4.10) yield
We next show that there exists $K(n)\ge 1$![]() such that for every $x\in U$
such that for every $x\in U$![]()
By ($W4$![]() ) we have
) we have
Now if $x\in U\setminus A_k^3$![]() , then $x\notin A_k^1$
, then $x\notin A_k^1$![]() and
and
Assume instead that $x\in A_k^3$![]() . Observe that $\bar u_k=0$
. Observe that $\bar u_k=0$![]() in $Q_{\eta \varepsilon _{k}}(x)\cap A_k^3$
in $Q_{\eta \varepsilon _{k}}(x)\cap A_k^3$![]() , so that
, so that
Furthermore, we can cover $Q_{\eta \varepsilon _{k}}(x)\cap (Q\setminus A_k^3)$![]() with a finite number $K(n)\ge 1$
with a finite number $K(n)\ge 1$![]() of balls of radius $\eta \varepsilon _{k}$
of balls of radius $\eta \varepsilon _{k}$![]() and centres $x_1,\ldots,x_{ K}\in U\setminus A_k^3$
and centres $x_1,\ldots,x_{ K}\in U\setminus A_k^3$![]() (see e.g. [Reference Scilla and Solombrino22, remark 2.8]). Hence, we find
(see e.g. [Reference Scilla and Solombrino22, remark 2.8]). Hence, we find

and (4.12) follows. Finally by (4.7), the monotonicity of $f_i^\eta$![]() , (4.13) we infer
, (4.13) we infer

where the last inequality follows from (4.12) and the fact that $f_i^\eta (t)\ge \frac {\alpha _im_\eta \eta ^n}{K} t$![]() when $t\le K \frac {\beta _i}{m_\eta \eta ^n \alpha _i}$
when $t\le K \frac {\beta _i}{m_\eta \eta ^n \alpha _i}$![]() . Moreover by using in order the change of variable $y=x-\eta \varepsilon _{k} z$
. Moreover by using in order the change of variable $y=x-\eta \varepsilon _{k} z$![]() , Fubini's theorem, and the change of variable $\hat x=x-\eta \varepsilon _kz$
, Fubini's theorem, and the change of variable $\hat x=x-\eta \varepsilon _kz$![]() (for $k$
(for $k$![]() large enough), we find
large enough), we find

Eventually gathering together (4.10), (4.14), and (4.15), we deduce (4.2) with
5. Lower bound
In this section we prove the lower bound. To this purpose it is convenient to localise the functionals $F_k$![]() , namely we set
, namely we set
Proposition 5.1 Lower bound: bulk contribution
Let $(u_k)\subset L^0(U;\mathbb {R}^n)$![]() be a sequence that converges in measure to $u\in L^0(U;\mathbb {R}^n)$
be a sequence that converges in measure to $u\in L^0(U;\mathbb {R}^n)$![]() . Assume moreover that $F_k(u_k)\le C$
. Assume moreover that $F_k(u_k)\le C$![]() and that (2.9) holds. Then, for $W$
and that (2.9) holds. Then, for $W$![]() as (2.9)
as (2.9)
Proof. Let $(u_k)$![]() and $u$
and $u$![]() be as in the statement. By proposition 4.1 $u\in GSBD^p(U)$
be as in the statement. By proposition 4.1 $u\in GSBD^p(U)$![]() . For every $k\in \mathbb {N}$
. For every $k\in \mathbb {N}$![]() let $\mu _k$
let $\mu _k$![]() be the Radon measure on $(U, \mathcal {B}(U))$
be the Radon measure on $(U, \mathcal {B}(U))$![]() given by
given by
As $\mu _k(A)\le C$![]() , by [Reference Ambrosio, Fusco and Pallara1, theorem 1.59] we deduce the existence of a subsequence, not relabelled, and of a Radon measure $\mu$
, by [Reference Ambrosio, Fusco and Pallara1, theorem 1.59] we deduce the existence of a subsequence, not relabelled, and of a Radon measure $\mu$![]() on $(A, \mathcal {B}(A))$
on $(A, \mathcal {B}(A))$![]() such that
such that
By Radon-Nikodym's Theorem (in the version of [Reference Ambrosio, Fusco and Pallara1, theorem 1.28]) there exist two measures $\mu ^a, \mu ^s$![]() with $\mu ^a\ll \mathcal {L}^n$
with $\mu ^a\ll \mathcal {L}^n$![]() and $\mu ^s\perp \mathcal {L}^n$
and $\mu ^s\perp \mathcal {L}^n$![]() , and a function $h\in L^1(A)$
, and a function $h\in L^1(A)$![]() such that $\mu =\mu ^a+\mu ^s$
such that $\mu =\mu ^a+\mu ^s$![]() and $\mu ^a=h \mathcal {L}^n$
and $\mu ^a=h \mathcal {L}^n$![]() . This together with (5.3) imply that
. This together with (5.3) imply that
Hence to conclude we need to show that
with $W$![]() as in (3.3). For $i\in \mathbb {N}$
as in (3.3). For $i\in \mathbb {N}$![]() fixed let $f_i(t)=\alpha _it\wedge \beta _i$
fixed let $f_i(t)=\alpha _it\wedge \beta _i$![]() be as in (2.3). Then it is enough to show that
be as in (2.3). Then it is enough to show that
We divide the proof of (5.5) into four steps. Step 1: In this step we show that for a.e. $x_0\in U$![]() there exists a sequence $(k_j,r_j)\to (+\infty,0)$
there exists a sequence $(k_j,r_j)\to (+\infty,0)$![]() as $j\to +\infty$
as $j\to +\infty$![]() such that setting $\delta _j:= \frac {\varepsilon _{k_j}}{r_j}$
such that setting $\delta _j:= \frac {\varepsilon _{k_j}}{r_j}$![]() ,
,
there hold
and
together with
By Besicovitch differentiation theorem and [Reference Cagnetti, Chambolle and Scardia6, corollary 5.2] we have that for a.e. $x_0\in U$![]() the following hold:
the following hold:
We fix $x_0\in \Omega$![]() for which (5.10) and (5.11) hold. By [Reference Ambrosio, Fusco and Pallara1, proposition 1.62] we have
for which (5.10) and (5.11) hold. By [Reference Ambrosio, Fusco and Pallara1, proposition 1.62] we have
for every $r>0$![]() , which together with (5.10) yield
, which together with (5.10) yield
Moreover from (5.2) and the change of variable $x=x_0+r x'$![]() we get
we get

From (5.6) and the change of variable $y=ry'$![]() we may deduce that
we may deduce that
Gathering together (5.12), (5.13), (5.14) and using (2.3) we obtain
Now, from (5.11) and the fact that $u_k$![]() converges to $u$
converges to $u$![]() in measure we can deduce that
in measure we can deduce that
If we fix a diagonal subsequence $(k_j,r_j)\to (+\infty,0)$![]() as $j\to +\infty$
as $j\to +\infty$![]() for which (5.8) and (5.9) hold, from (5.15) we also get (5.7) for $\delta _j:= \tfrac {\varepsilon _{k_j}}{r_j}$
for which (5.8) and (5.9) hold, from (5.15) we also get (5.7) for $\delta _j:= \tfrac {\varepsilon _{k_j}}{r_j}$![]() (up to taking a further subsequence to have a limit in place of a limsup). With this, the proof of step 1 is concluded.
(up to taking a further subsequence to have a limit in place of a limsup). With this, the proof of step 1 is concluded.
Step 2: In this step we show that for any $0<\zeta <1$![]() and a.e. $x_0\in U$
and a.e. $x_0\in U$![]() there exist $(\bar u_j)\subset GSBV^p(Q;\mathbb {R}^n)$
there exist $(\bar u_j)\subset GSBV^p(Q;\mathbb {R}^n)$![]() and $c_0>0$
and $c_0>0$![]() independent of $j$
independent of $j$![]() such that
such that
By step 1 we have that $u_{k_j}^{r_j}$![]() converges in measure to $\nabla u(x_0)(\cdot )$
converges in measure to $\nabla u(x_0)(\cdot )$![]() in $Q$
in $Q$![]() as $j\to +\infty$
as $j\to +\infty$![]() and for $j$
and for $j$![]() large enough it satisfies
large enough it satisfies
Next we fix $\eta \in (0,1)$![]() such that $Q_\eta (0)\subset \subset S$
such that $Q_\eta (0)\subset \subset S$![]() and let $m_\eta$
and let $m_\eta$![]() and $f_i^\eta$
and $f_i^\eta$![]() be as in (4.6). Then we get
be as in (4.6). Then we get

We define the sets

Then arguing as in the proof of proposition 4.1 we find that

(5.22) together with (5.20) and (5.21) imply that (for $j$![]() large enough)
large enough)
By the coarea formula and the mean value theorem we can find $t_j\in (0,(1-\eta )\delta _{j})$![]() such that setting $A_j^3:= \{\operatorname {dist}(\cdot,A_j^1)\le t_j \}\subset A_j^2$
such that setting $A_j^3:= \{\operatorname {dist}(\cdot,A_j^1)\le t_j \}\subset A_j^2$![]()
We finally define

Recall that, by definition, $\frac {\varepsilon _j}{\delta _j}\to 0$![]() . With this, as a consequence of (5.23) and (5.24) we have that both $\mathcal {L}^n( A_j^3)$
. With this, as a consequence of (5.23) and (5.24) we have that both $\mathcal {L}^n( A_j^3)$![]() and $\mathcal {H}^{n-1}(\partial A_j^3)=\mathcal {H}^{n-1}(J_{\bar u_j})$
and $\mathcal {H}^{n-1}(\partial A_j^3)=\mathcal {H}^{n-1}(J_{\bar u_j})$![]() converge to $0$
converge to $0$![]() as $j\to +\infty$
as $j\to +\infty$![]() . Hence $\bar u_j\subset GSBV^p(Q;\mathbb {R}^n)$
. Hence $\bar u_j\subset GSBV^p(Q;\mathbb {R}^n)$![]() and $\bar u_j-u_{k_j}^{r_j}\to 0$
and $\bar u_j-u_{k_j}^{r_j}\to 0$![]() in measure on $Q$
in measure on $Q$![]() which combined with (5.8) yield $\bar u_j\to \nabla u(x_0)(\cdot )$
which combined with (5.8) yield $\bar u_j\to \nabla u(x_0)(\cdot )$![]() in measure on $Q$
in measure on $Q$![]() . It remains to show (5.19). To this aim notice that arguing exactly as in the proof of proposition 4.1 one can find $K(n)\ge 1$
. It remains to show (5.19). To this aim notice that arguing exactly as in the proof of proposition 4.1 one can find $K(n)\ge 1$![]() such that for every $x\in \overline Q$
such that for every $x\in \overline Q$![]()

Next from (5.21) and the monotonicity of $f_i^\eta$![]() we infer
we infer

where the last inequality follows from (5.25) and fact that $f_i^\eta (t)\ge \frac {\alpha _im_\eta \eta ^n}{K} t$![]() when $t\le K \frac {\beta _i}{m_\eta \eta ^n \alpha _i}$
when $t\le K \frac {\beta _i}{m_\eta \eta ^n \alpha _i}$![]() . Finally, for a fixed $0<\zeta <1$
. Finally, for a fixed $0<\zeta <1$![]() , arguing exactly as for (4.15) we get
, arguing exactly as for (4.15) we get

when $j$![]() is sufficiently large. Eventually gathering together (5.20), (5.26), and (5.27), we deduce (5.19) with $c_0:= \frac {CK}{c_1\alpha _im_\eta \eta ^n}$
is sufficiently large. Eventually gathering together (5.20), (5.26), and (5.27), we deduce (5.19) with $c_0:= \frac {CK}{c_1\alpha _im_\eta \eta ^n}$![]() .
.
Step 3: In this step show that for a.e. $x_0\in U$![]() there exists a sequence $(w_j)\subset W^{1,p}(Q;\mathbb {R}^n)$
there exists a sequence $(w_j)\subset W^{1,p}(Q;\mathbb {R}^n)$![]() such that:
such that:
From step 2 we can apply [Reference Friedrich, Perugini and Solombrino18, lemma 5.1] to the sequence $\bar u_j$![]() and get the existence of $(w_j)\subset W^{1,p}(Q;\mathbb {R}^n)$
and get the existence of $(w_j)\subset W^{1,p}(Q;\mathbb {R}^n)$![]() that satisfies (5.28)–(5.30). Moreover recalling ($W4$
that satisfies (5.28)–(5.30). Moreover recalling ($W4$![]() ) and the equi-integrability of $(|\nabla w_j|^p)$
) and the equi-integrability of $(|\nabla w_j|^p)$![]() we have that $W_{k_j}^{r_j}(x,e(w_j))$
we have that $W_{k_j}^{r_j}(x,e(w_j))$![]() is equi-integrable as well, while from the inclusion
is equi-integrable as well, while from the inclusion
it follows that $\mathcal {L}^n( \left \{ e(w_j)\ne e( u_{k_j}^{r_j} )\right \})\to 0$![]() . Thus, we can apply lemma 3.6 with $g_j=W_{k_j}^{r_j}(x,e(w_j))$
. Thus, we can apply lemma 3.6 with $g_j=W_{k_j}^{r_j}(x,e(w_j))$![]() , and $E_j=\left \{ e(w_j)\ne e( u_{k_j}^{r_j} )\right \}$
, and $E_j=\left \{ e(w_j)\ne e( u_{k_j}^{r_j} )\right \}$![]() , and deduce that
, and deduce that
We also remark that by the definition of $E_j$![]() we have
we have

By monotonicity of $f_i$![]() and since $f_i(t)\le \alpha _it$
and since $f_i(t)\le \alpha _it$![]() we obtain the following estimate
we obtain the following estimate

Passing to the limit as $j\to +\infty$![]() in the above inequality and using (5.7) and (5.32) we infer (5.31).
in the above inequality and using (5.7) and (5.32) we infer (5.31).
Step 4: In this step we show that for a.e. $x_0\in U$![]()

We define the following partition
Since $f_i(t)=\alpha _it$![]() when $t\le \frac {\beta _i}{\alpha _i}$
when $t\le \frac {\beta _i}{\alpha _i}$![]() , and $(W_{k_j}^{r_j}(\cdot,e(w_j))\chi _{B_j^2})*\rho _{\delta _{j}}\le \frac {\beta _i}{\alpha _i}$
, and $(W_{k_j}^{r_j}(\cdot,e(w_j))\chi _{B_j^2})*\rho _{\delta _{j}}\le \frac {\beta _i}{\alpha _i}$![]() by definition of $B^2_j$
by definition of $B^2_j$![]() and standard properties of the convolution, we have
and standard properties of the convolution, we have

As for $j$![]() large enough there holds $\mathcal {L}^n( B_j^1)\le Cr_j\delta _{j}\to 0$
large enough there holds $\mathcal {L}^n( B_j^1)\le Cr_j\delta _{j}\to 0$![]() , lemma 3.6 implies
, lemma 3.6 implies
Now, taking the liminf as $j\to +\infty$![]() in (5.34), and adding the vanishing term in (5.35) to the right-hand side, we get
in (5.34), and adding the vanishing term in (5.35) to the right-hand side, we get

From this, applying lemma 3.7 with $g_j=W_{k_j}^{r_j}(x,e(w_j))$![]() we have
we have

Next we modify $w_j$![]() so that it coincides with $\nabla u(x_0)(\cdot )$
so that it coincides with $\nabla u(x_0)(\cdot )$![]() on $\partial Q_{1-\zeta }(0)$
on $\partial Q_{1-\zeta }(0)$![]() without essentially increasing the energy. This can be achieved by relying on the following Fundamental Estimate than can be proved with standard arguments: for given $\gamma >0$
without essentially increasing the energy. This can be achieved by relying on the following Fundamental Estimate than can be proved with standard arguments: for given $\gamma >0$![]() , there exist $C(\gamma )$
, there exist $C(\gamma )$![]() and a sequence $(\overline w_j)\subset W^{1,p}(Q_{1-\zeta }(0);\mathbb {R}^d)$
and a sequence $(\overline w_j)\subset W^{1,p}(Q_{1-\zeta }(0);\mathbb {R}^d)$![]() with $\overline w_i=\nabla u(x_0)(\cdot )$
with $\overline w_i=\nabla u(x_0)(\cdot )$![]() in a neighbourhood of $\partial Q_{1-\zeta }(0)$
in a neighbourhood of $\partial Q_{1-\zeta }(0)$![]() such that
such that

By (5.30) we know that $w_j$![]() converges to $\nabla u(x_0)(\cdot )$
converges to $\nabla u(x_0)(\cdot )$![]() in $L^p(Q)$
in $L^p(Q)$![]() , moreover from ($W4$
, moreover from ($W4$![]() ) there holds
) there holds

This fact and (5.38) imply that

We now set $\widetilde w_j(x):= r_j\overline w_j((x-x_0)/r_j)$![]() , which is admissible for $\mathbf {m}_{k_j}(u_{\nabla u(x_0)}, Q_{(1-\zeta )r_j}(0))$
, which is admissible for $\mathbf {m}_{k_j}(u_{\nabla u(x_0)}, Q_{(1-\zeta )r_j}(0))$![]() in (2.6). Hence, by a change of variable in (5.39) we obtain
in (2.6). Hence, by a change of variable in (5.39) we obtain

Gathering together (5.39) and (5.40), with (5.9) we deduce

With this, (5.36), and (5.37), we eventually deduce (5.33) by arbitrariness of $\zeta$![]() and $\gamma$
and $\gamma$![]() .
.
Conclusion: from step 3 and step 4 we deduce the validity of (5.5) and the proof is concluded.
Remark 5.2 We observe en passant that proposition 5.1 indeed holds also for a sequence of functionals
provided the functions $f_k$![]() satisfy an estimate of the form
satisfy an estimate of the form
for all $t\in [0,+\infty )$![]() , where $\beta$
, where $\beta$![]() is a uniform constant and $\alpha =\lim _{k\to +\infty }\alpha _k$
is a uniform constant and $\alpha =\lim _{k\to +\infty }\alpha _k$![]() .
.
Proposition 5.3 Lower bound: surface contribution
Let $(u_k)\subset L^0(U;\mathbb {R}^n)$![]() be a sequence that converges to in measure to $u\in L^0(U;\mathbb {R}^n)$
be a sequence that converges to in measure to $u\in L^0(U;\mathbb {R}^n)$![]() . Assume moreover that $F_k(u_k)\le C$
. Assume moreover that $F_k(u_k)\le C$![]() . Then there holds
. Then there holds
Proof. Let $(u_k)$![]() and $u$
and $u$![]() be as in the statement, so that by proposition 4.1 $u\in GSBD^p(U)$
be as in the statement, so that by proposition 4.1 $u\in GSBD^p(U)$![]() . Let $A\in \mathcal {A}(U)$
. Let $A\in \mathcal {A}(U)$![]() be fixed. We claim that it suffices to show that for any $\xi \in \mathbb {S}^{n-1}$
be fixed. We claim that it suffices to show that for any $\xi \in \mathbb {S}^{n-1}$![]() fixed there holds
fixed there holds
with
Indeed, assume for the moment (5.41) holds true. Then ($W4$![]() ) gives
) gives
Since $f$![]() is nondecreasing, the above implies
is nondecreasing, the above implies

with $\varphi _\xi \colon J_u\to [0,+\infty ]$![]() given by
given by

Now let $(\xi _h)\subset \mathbb {S}^{n-1}$![]() be a dense subset, in this way by [Reference Braides5, proposition 1.16] it holds
be a dense subset, in this way by [Reference Braides5, proposition 1.16] it holds
On the other hand by [Reference Negri20, lemma 4.5], we have
which in turn implies $\phi _\rho (\nu _u(x))=\sup _h\varphi _{\xi _h}(x)$![]() and the thesis follows. It remains to show (5.41) for which we will argue by slicing. As the set $S$
and the thesis follows. It remains to show (5.41) for which we will argue by slicing. As the set $S$![]() is convex for $\delta \in (0,1)$
is convex for $\delta \in (0,1)$![]() fixed we can find $r=r(\delta,S)$
fixed we can find $r=r(\delta,S)$![]() such that the cylinder
such that the cylinder
where $R_\xi \in SO(n)$![]() is such that $R_\xi e_n=\xi$
is such that $R_\xi e_n=\xi$![]() [see (j)]. Let now $m_\xi := \min _{x\in \overline {C}_\xi ^{r,\delta }}\rho (x)$
[see (j)]. Let now $m_\xi := \min _{x\in \overline {C}_\xi ^{r,\delta }}\rho (x)$![]() and
and
Next for any $x\in A$![]() we denote by $\hat x_\xi$
we denote by $\hat x_\xi$![]() the projection of $x$
the projection of $x$![]() onto $\Pi ^\xi := \{y\in \mathbb {R}^n\colon \langle y,\xi \rangle =0\}$
onto $\Pi ^\xi := \{y\in \mathbb {R}^n\colon \langle y,\xi \rangle =0\}$![]() and
and
Then we have

where the last equality follows by Fubini's Theorem. Noticing that $f$![]() is concave and using the change of variable $z=\hat x_\xi +s\xi +\varepsilon _krz'$
is concave and using the change of variable $z=\hat x_\xi +s\xi +\varepsilon _krz'$![]() with
with
together with Jensen's inequality yield

with $\widetilde f(t):=f\left (\frac {c_1m_\xi }{r^{n-1}}t\right )$![]() and $w_{\xi,k}(\hat x_\xi, z',s):= \langle u_k(\hat x_\xi +\varepsilon _krz'+s\xi ),\xi \rangle$
and $w_{\xi,k}(\hat x_\xi, z',s):= \langle u_k(\hat x_\xi +\varepsilon _krz'+s\xi ),\xi \rangle$![]() . Observe now that applying corollary 3.9 and Fubini's Theorem to the functions $w_{\xi,k}(\hat x_\xi, z',s)$
. Observe now that applying corollary 3.9 and Fubini's Theorem to the functions $w_{\xi,k}(\hat x_\xi, z',s)$![]() we have that, for a.e. $(\hat x_\xi, z')\in \Pi _\xi \times Q'_{\xi }$
we have that, for a.e. $(\hat x_\xi, z')\in \Pi _\xi \times Q'_{\xi }$![]() the functions $s\mapsto w_{\xi,k}(\hat x_\xi, z',s)$
the functions $s\mapsto w_{\xi,k}(\hat x_\xi, z',s)$![]() converge to the section $u^{\hat x_\xi }(s):=\langle u(\hat x_\xi +s\xi ), \xi \rangle$
converge to the section $u^{\hat x_\xi }(s):=\langle u(\hat x_\xi +s\xi ), \xi \rangle$![]() in measure on $I_\xi$
in measure on $I_\xi$![]() . Further, gathering together (5.43) and (5.44), and exchanging the order of integration it holds
. Further, gathering together (5.43) and (5.44), and exchanging the order of integration it holds

where the shortcut $w^{\hat x_\xi, z'}_{\xi,k}(s)$![]() denotes the function $s\mapsto w_{\xi,k}(\hat x_\xi, z',s)$
denotes the function $s\mapsto w_{\xi,k}(\hat x_\xi, z',s)$![]() for fixed $(\hat x_\xi, z')$
for fixed $(\hat x_\xi, z')$![]() . By theorem 3.3 we get
. By theorem 3.3 we get

Combining (5.45) with (5.46), we finally obtain
Eventually by the arbitrariness of $\delta$![]() , we deduce (5.41).
, we deduce (5.41).
With the help of propositions 5.1 and 5.3 we can now prove the following lower bound.
Proposition 5.4 Lower-bound
Let $F_k$![]() and $F$
and $F$![]() be as in (2.5) and (2.10) respectively. Let $(u_k)\subset L^0(U;\mathbb {R}^n)$
be as in (2.5) and (2.10) respectively. Let $(u_k)\subset L^0(U;\mathbb {R}^n)$![]() and $u$
and $u$![]() be such that $u_k$
be such that $u_k$![]() converges to $u$
converges to $u$![]() in measure. Then there exists a subsequence, not relabelled, such that
in measure. Then there exists a subsequence, not relabelled, such that
Proof. The result can be obtained exactly as in [Reference Scilla and Solombrino22, proposition 5.4].
6. Upper bound
In this section we prove the upper bound.
Proposition 6.1 Let $F_k$![]() and $F$
and $F$![]() be as in (2.5) and (2.10) respectively. Then for each $u\in L^0(U;\mathbb {R}^n)$
be as in (2.5) and (2.10) respectively. Then for each $u\in L^0(U;\mathbb {R}^n)$![]() there is $(u_k)\subset L^0(U;\mathbb {R}^n)$
there is $(u_k)\subset L^0(U;\mathbb {R}^n)$![]() that converges in measure to $u$
that converges in measure to $u$![]() and such that
and such that
Proof. Without loss of generality we assume $F(u)< C$![]() so that $u\in GSBD^p(U)$
so that $u\in GSBD^p(U)$![]() . Moreover, since $W$
. Moreover, since $W$![]() has $p$
has $p$![]() -growth from above, by theorem 3.4 we can assume that $u\in \mathcal {W}^\infty _{\rm pw}(U;\mathbb {R}^n)$
-growth from above, by theorem 3.4 we can assume that $u\in \mathcal {W}^\infty _{\rm pw}(U;\mathbb {R}^n)$![]() and that $J_u$
and that $J_u$![]() is an essentially closed connected $(n-1)$
is an essentially closed connected $(n-1)$![]() -rectifiable set compactly contained in $U$
-rectifiable set compactly contained in $U$![]() , since the above subspace is dense in energy. We fix $U'\in \mathcal {A}$
, since the above subspace is dense in energy. We fix $U'\in \mathcal {A}$![]() with $U\subset \subset U'$
with $U\subset \subset U'$![]() and consider an extension of $u$
and consider an extension of $u$![]() on $U'$
on $U'$![]() , not relabelled, such that $u\in \mathcal {W}^\infty _{\rm pw}(U';\mathbb {R}^n)$
, not relabelled, such that $u\in \mathcal {W}^\infty _{\rm pw}(U';\mathbb {R}^n)$![]() . Then by theorem 3.1 and remark 3.2 we can find $(v_k)\subset W^{1,p}(U'\setminus \overline {J_u};\mathbb {R}^n)$
. Then by theorem 3.1 and remark 3.2 we can find $(v_k)\subset W^{1,p}(U'\setminus \overline {J_u};\mathbb {R}^n)$![]() such that $v_k$
such that $v_k$![]() converges strongly to $u$
converges strongly to $u$![]() in $L^p(U'\setminus J_u;\mathbb {R}^n)$
in $L^p(U'\setminus J_u;\mathbb {R}^n)$![]() and
and
where the last equality clearly holds as $J_u$![]() is a null set. For every $h>0$
is a null set. For every $h>0$![]() we set
we set
so that for $h$![]() small enough $(J_u)_h\subset \subset U$
small enough $(J_u)_h\subset \subset U$![]() . Fix now $0<\delta _k<<\varepsilon _k$
. Fix now $0<\delta _k<<\varepsilon _k$![]() and take $\varphi _k\in C^\infty _c(U')$
and take $\varphi _k\in C^\infty _c(U')$![]() a cutoff between $(J_u)_{\delta _k}$
a cutoff between $(J_u)_{\delta _k}$![]() and $(J_u)_{2\delta _k}$
and $(J_u)_{2\delta _k}$![]() . Next define $(u_k)\subset W^{1,p}(U';\mathbb {R}^n)$
. Next define $(u_k)\subset W^{1,p}(U';\mathbb {R}^n)$![]() as
as
and in particular $u_k\to u$![]() in measure on $U'$
in measure on $U'$![]() . Then using that $u_k=v_k$
. Then using that $u_k=v_k$![]() in $U'\setminus (J_u)_{2\delta _k}$
in $U'\setminus (J_u)_{2\delta _k}$![]() we have
we have
Now invoking [Reference Villa and Lussardi23, theorem 3.7] we have
Fix $\hat \alpha >\alpha$![]() . With (2.2), the change of variable $y=x-\varepsilon _kz$
. With (2.2), the change of variable $y=x-\varepsilon _kz$![]() , Fubini's theorem, and the change of variable $\hat x=x-\varepsilon _k z$
, Fubini's theorem, and the change of variable $\hat x=x-\varepsilon _k z$![]() we have
we have

Hence passing to the limit in $k$![]() in the above inequality and using (6.1) we get
in the above inequality and using (6.1) we get
for all $\hat \alpha >\alpha$![]() . Finally gathering together (6.2)–(6.4), we obtain
. Finally gathering together (6.2)–(6.4), we obtain
Eventually by the arbitrariness of $U'$![]() and $\hat \alpha$
and $\hat \alpha$![]() , we conclude.
, we conclude.
Remark 6.2 If a lower order term $\int _U\psi (|u|)\,{\rm d}x$![]() , is added to the energy, the density argument above can still be applied if $\psi$
, is added to the energy, the density argument above can still be applied if $\psi$![]() complies with the assumptions of theorem 3.4. Also observe that within the same assumptions, $\int _U\psi (|u_k|)\,{\rm d}x$
complies with the assumptions of theorem 3.4. Also observe that within the same assumptions, $\int _U\psi (|u_k|)\,{\rm d}x$![]() is equiintegrable whenever $(u_k)$
is equiintegrable whenever $(u_k)$![]() is converging in $L^p$
is converging in $L^p$![]() . For $u_k$
. For $u_k$![]() and $u$
and $u$![]() as in the proof above, this entails the convergence $\int _U\psi (|u_k|)\,{\rm d}x\to \int _U\psi (|u|)\,{\rm d}x$
as in the proof above, this entails the convergence $\int _U\psi (|u_k|)\,{\rm d}x\to \int _U\psi (|u|)\,{\rm d}x$![]() .
.
We are now in a position to prove theorem 2.1.
7. Stochastic homogenisation
In this section we are concerned with the $\Gamma$![]() -convergence analysis of the functionals $F_k$
-convergence analysis of the functionals $F_k$![]() when $W_k$
when $W_k$![]() are random integrands of type
are random integrands of type
with $\omega$![]() belonging to the sample space $\Omega$
belonging to the sample space $\Omega$![]() of a complete probability space $(\Omega,\mathcal {T},P)$
of a complete probability space $(\Omega,\mathcal {T},P)$![]() and $\delta _k\searrow 0$
and $\delta _k\searrow 0$![]() . In order to do that we first give some definitions.
. In order to do that we first give some definitions.
Definition 7.1 Group of $P$![]() -preserving transformations
-preserving transformations
A group of $P$![]() -preserving transformations on $(\Omega,\mathcal {T},P)$
-preserving transformations on $(\Omega,\mathcal {T},P)$![]() is a family $(\tau _z)_{z\in \mathbb {Z}^n}$
is a family $(\tau _z)_{z\in \mathbb {Z}^n}$![]() of mappings $\tau _z\colon \Omega \to \Omega$
of mappings $\tau _z\colon \Omega \to \Omega$![]() satisfying the following:
satisfying the following:
(a) (measurability) $\tau _z$
 is $\mathcal {T}$
is $\mathcal {T}$ -measurable for every $z\in \mathbb {Z}^n$
-measurable for every $z\in \mathbb {Z}^n$ ;
;(b) (invariance) $P(\tau _z(E))=P(E)$
 , for every $E\in \mathcal {T}$
, for every $E\in \mathcal {T}$ and every $z\in \mathbb {Z}^n$
and every $z\in \mathbb {Z}^n$ ;
;(c) (group property) $\tau _0={\rm id}_{\Omega}$
 and $\tau _{z+z'}=\tau _z\circ \tau _{z'}$
and $\tau _{z+z'}=\tau _z\circ \tau _{z'}$ for every $z,z'\in \mathbb {Z}^n$
for every $z,z'\in \mathbb {Z}^n$ .
.
If in addition, every $(\tau _z)_{z\in \mathbb {Z}^n}$![]() -invariant set (that is, every $E\in \mathcal {T}$
-invariant set (that is, every $E\in \mathcal {T}$![]() with $\tau _z(E)=E$
with $\tau _z(E)=E$![]() for every $z\in \mathbb {Z}^n$
for every $z\in \mathbb {Z}^n$![]() ) has probability 0 or 1, then $(\tau _z)_{z\in \mathbb {Z}^n}$
) has probability 0 or 1, then $(\tau _z)_{z\in \mathbb {Z}^n}$![]() is called ergodic.
is called ergodic.
Let $a:= (a_1,\dots,a_n),\,b:= (b_1,\dots,b_n)\in \mathbb {Z}^n$![]() with $a_i< b_i$
with $a_i< b_i$![]() for all $i\in \{1,\ldots,n\}$
for all $i\in \{1,\ldots,n\}$![]() ; we define the $n$
; we define the $n$![]() -dimensional interval
-dimensional interval
and we set
Definition 7.2 Subadditive process
A discrete subadditive process with respect to a group $(\tau _z)_{z\in \mathbb {Z}^n}$![]() of $P$
of $P$![]() -preserving transformations on $(\Omega,\mathcal {T},P)$
-preserving transformations on $(\Omega,\mathcal {T},P)$![]() is a function $\mu \colon \Omega \times \mathcal {I}_n\to \mathbb {R}$
is a function $\mu \colon \Omega \times \mathcal {I}_n\to \mathbb {R}$![]() satisfying the following:
satisfying the following:
(a) (measurability) for every $A\in \mathcal {I}_n$
 the function $\omega \mapsto \mu (\omega,A)$
the function $\omega \mapsto \mu (\omega,A)$ is $\mathcal {T}$
is $\mathcal {T}$ -measurable;
-measurable;(b) (covariance) for every $\omega \in \Omega$
 , $A\in \mathcal {I}_n$
, $A\in \mathcal {I}_n$ , and $z\in \mathbb {Z}^n$
, and $z\in \mathbb {Z}^n$ we have $\mu (\omega,A+z)=\mu (\tau _z(\omega ),A)$
we have $\mu (\omega,A+z)=\mu (\tau _z(\omega ),A)$ ;
;(c) (subadditivity) for every $A\in \mathcal {I}_n$
 and for every finite family $(A_i)_{i\in I}\subset \mathcal {I}_n$
and for every finite family $(A_i)_{i\in I}\subset \mathcal {I}_n$ of pairwise disjoint sets such that $A=\cup _{i\in I}A_i$
of pairwise disjoint sets such that $A=\cup _{i\in I}A_i$ , we have
\[ \mu(\omega,A)\le\sum_{i\in I}\mu(\omega,A_i)\quad\text{for every}\,\,\omega\in\Omega\,; \]
, we have
\[ \mu(\omega,A)\le\sum_{i\in I}\mu(\omega,A_i)\quad\text{for every}\,\,\omega\in\Omega\,; \]
(d) (boundedness) there exists $c>0$
 such that $0\le \mu (\omega,A)\le c\mathcal {L}^n(A)$
such that $0\le \mu (\omega,A)\le c\mathcal {L}^n(A)$ for every $\omega \in \Omega$
for every $\omega \in \Omega$ and $A\in \mathcal {I}_n$
and $A\in \mathcal {I}_n$ .
.
Definition 7.3 Stationarity
Let $(\tau _z)_{z\in \mathbb {Z}^n}$![]() be a group of $P$
be a group of $P$![]() -preserving transformations on $(\Omega,\mathcal {T},P)$
-preserving transformations on $(\Omega,\mathcal {T},P)$![]() . We say that $W\colon \Omega \times \mathbb {R}^n\times \mathbb {M}^{n\times n}\to [0,+\infty )$
. We say that $W\colon \Omega \times \mathbb {R}^n\times \mathbb {M}^{n\times n}\to [0,+\infty )$![]() is stationary with respect to $(\tau _z)_{z\in \mathbb {Z}^n}$
is stationary with respect to $(\tau _z)_{z\in \mathbb {Z}^n}$![]() if
if
for every $\omega \in \Omega$![]() , $x\in \mathbb {R}^n$
, $x\in \mathbb {R}^n$![]() , $z\in \mathbb {Z}^n$
, $z\in \mathbb {Z}^n$![]() and $M\in \mathbb {M}^{n\times n}$
and $M\in \mathbb {M}^{n\times n}$![]() . Moreover we say that a stationary random integrand $W$
. Moreover we say that a stationary random integrand $W$![]() is ergodic if $(\tau _z)_{z\in \mathbb {Z}^n}$
is ergodic if $(\tau _z)_{z\in \mathbb {Z}^n}$![]() is ergodic.
is ergodic.
For our purposes we consider random integrands $W\colon \Omega \times \mathbb {R}^n\times \mathbb {M}^{n\times n}\to [0,+\infty )$![]() satisfying the following assumptions:
satisfying the following assumptions:
(W1) $W$
 is $(\mathcal {T}\otimes \mathcal {B}^n\otimes \mathcal {B}^{n\times n})$
is $(\mathcal {T}\otimes \mathcal {B}^n\otimes \mathcal {B}^{n\times n})$ -measurable;
-measurable;(W2) $W(\omega,\cdot,\cdot )\in \mathcal {W}$
 for every $\omega \in \Omega$
for every $\omega \in \Omega$ ;
;(W3) the map $M\mapsto W(\omega,x,M)$
 is lower semicontinuous for every $\omega \in \Omega$
is lower semicontinuous for every $\omega \in \Omega$ and every $x\in \mathbb {R}^n$
and every $x\in \mathbb {R}^n$ .
.
Let $W$![]() be a random integrand satisfying ($w1$
be a random integrand satisfying ($w1$![]() )–($w3$
)–($w3$![]() ) and $\delta _k\searrow 0$
) and $\delta _k\searrow 0$![]() . We consider the family of functionals $F_k(\omega )\colon L^0(U;\mathbb {R}^n)\to [0,+\infty ]$
. We consider the family of functionals $F_k(\omega )\colon L^0(U;\mathbb {R}^n)\to [0,+\infty ]$![]() defined as
defined as
if $u\in W^{1,p}(U;\mathbb {R}^n)$![]() , and extended to $+\infty$
, and extended to $+\infty$![]() otherwise. Let also for $\omega \in \Omega$
otherwise. Let also for $\omega \in \Omega$![]() and $A\in \mathcal {A}$
and $A\in \mathcal {A}$![]()
We now state the main theorem of this section.
Theorem 7.4 Stochastic homogenisation
Let $W$![]() be a random integrand satisfying ($w1$
be a random integrand satisfying ($w1$![]() )–($w3$
)–($w3$![]() ). Assume moreover $W$
). Assume moreover $W$![]() is stationary with respect to a group $(\tau _z)_{z\in \mathbb {Z}^n}$
is stationary with respect to a group $(\tau _z)_{z\in \mathbb {Z}^n}$![]() of $P$
of $P$![]() -preserving transformations on $(\Omega,\mathcal {T},P)$
-preserving transformations on $(\Omega,\mathcal {T},P)$![]() . For every $\omega \in \Omega$
. For every $\omega \in \Omega$![]() let $F_k(\omega )$
let $F_k(\omega )$![]() be as in (7.1) and $\mathbf {m}_\omega$
be as in (7.1) and $\mathbf {m}_\omega$![]() be as in (7.2). Then there exists $\Omega '\in \mathcal {T}$
be as in (7.2). Then there exists $\Omega '\in \mathcal {T}$![]() , with $P(\Omega ')=1$
, with $P(\Omega ')=1$![]() such that for every $\omega \in \Omega '$
such that for every $\omega \in \Omega '$![]() , $x\in \mathbb {R}^n$
, $x\in \mathbb {R}^n$![]() , $M\in \mathbb {M}^{n\times n}$
, $M\in \mathbb {M}^{n\times n}$![]() the limit
the limit
exists and is independent of $x$![]() . The function $W_{\rm hom}\colon \Omega \times \mathbb {M}^{n\times n}\to [0,+\infty )$
. The function $W_{\rm hom}\colon \Omega \times \mathbb {M}^{n\times n}\to [0,+\infty )$![]() is $({\mathcal {T}\otimes \mathcal {B}^{n\times n}})$
is $({\mathcal {T}\otimes \mathcal {B}^{n\times n}})$![]() -measurable. Moreover, for every $\omega \in \Omega '$
-measurable. Moreover, for every $\omega \in \Omega '$![]() the functionals $F_k(\omega )$
the functionals $F_k(\omega )$![]() $\Gamma$
$\Gamma$![]() -converge in measure to the functional $F_{\rm hom}(\omega )\colon L^0(U;\mathbb {R}^n)\to [0,+\infty ]$
-converge in measure to the functional $F_{\rm hom}(\omega )\colon L^0(U;\mathbb {R}^n)\to [0,+\infty ]$![]() given by
given by

If, in addition, $W$![]() is ergodic, then $W_{\rm hom}$
is ergodic, then $W_{\rm hom}$![]() is independent of $\omega$
is independent of $\omega$![]() and
and
and thus $F_{\rm hom}$![]() is deterministic.
is deterministic.
The proof of theorem 7.4 is quite standard and can be achieved as in [Reference Dal Maso and Modica12] (see also [Reference Ruf and Ruf21]). For this reason here we only detail the main adaptations.
Proposition 7.5 Let $W$![]() be a stationary random integrand satisfying ($w1$
be a stationary random integrand satisfying ($w1$![]() )–($w3$
)–($w3$![]() ) and let $\mathbf {m}_\omega$
) and let $\mathbf {m}_\omega$![]() be as in (7.2). Then for every $M\in \mathbb {M}^{n\times n}$
be as in (7.2). Then for every $M\in \mathbb {M}^{n\times n}$![]() the function $\mu _M\colon \Omega \times \mathcal {I}_n\to \mathbb {R}$
the function $\mu _M\colon \Omega \times \mathcal {I}_n\to \mathbb {R}$![]() given by $\mu _M(\omega,A):= \mathbf {m}_\omega (u_M,A)$
given by $\mu _M(\omega,A):= \mathbf {m}_\omega (u_M,A)$![]() defines a subadditive process on $(\Omega,\mathcal {T},P)$
defines a subadditive process on $(\Omega,\mathcal {T},P)$![]() . Moreover
. Moreover
for $P$![]() -a.e. $\omega \in \Omega$
-a.e. $\omega \in \Omega$![]() and for every $A\in \mathcal {I}_n$
and for every $A\in \mathcal {I}_n$![]() .
.
Proof. Let $M\in \mathbb {M}^{n\times n}$![]() be fixed. Then we need to show that $\mu _M$
be fixed. Then we need to show that $\mu _M$![]() satisfies properties (a)–(d). The proof of properties (b)–(d) and of (7.5) are standard and therefore we omit it here. It then remains to prove (a). Let $A\in \mathcal {I}_n$
satisfies properties (a)–(d). The proof of properties (b)–(d) and of (7.5) are standard and therefore we omit it here. It then remains to prove (a). Let $A\in \mathcal {I}_n$![]() be fixed. For $N\in \mathbb {N}$
be fixed. For $N\in \mathbb {N}$![]() let
let
be the Moreau-Yosida regularisation of $M\mapsto W(\omega,x,M)$![]() which is $N$
which is $N$![]() -Lipschitz. Let also
-Lipschitz. Let also
be defined as
Arguing as in the proof of [Reference Ruf and Ruf21, lemma C.1.] it can be shown that $(\omega,u)\mapsto F^N(\omega )(u)$![]() is $\mathcal {T}\otimes \mathcal {B}(W^{1,p}(A))$
is $\mathcal {T}\otimes \mathcal {B}(W^{1,p}(A))$![]() -measurable. By ($w3$
-measurable. By ($w3$![]() ) $W^N\nearrow W$
) $W^N\nearrow W$![]() pointwise, and in particular $F^N(\omega )(u)$
pointwise, and in particular $F^N(\omega )(u)$![]() converges to $\int _AW(\omega,x,e(u))\,{\rm d}x$
converges to $\int _AW(\omega,x,e(u))\,{\rm d}x$![]() pointwise. As a consequence $(\omega,u)\mapsto \int _AW(\omega,x,e(u))\,{\rm d}x$
pointwise. As a consequence $(\omega,u)\mapsto \int _AW(\omega,x,e(u))\,{\rm d}x$![]() is also $\mathcal {T}\otimes \mathcal {B}(W^{1,p}(A))$
is also $\mathcal {T}\otimes \mathcal {B}(W^{1,p}(A))$![]() -measurable. Now we note that $F(\omega )(u_M)<+\infty$
-measurable. Now we note that $F(\omega )(u_M)<+\infty$![]() . This together with ($w3$
. This together with ($w3$![]() ) and [Reference Ruf and Ruf21, lemma C.2.] imply that $\omega \mapsto \mu _M(u_M,A)$
) and [Reference Ruf and Ruf21, lemma C.2.] imply that $\omega \mapsto \mu _M(u_M,A)$![]() is $\mathcal {T}$
is $\mathcal {T}$![]() -measurable.
-measurable.
The proof of theorem 7.4 follows by proposition 7.5 and the Subadditive Ergodic Theorem [Reference Krengel and Akcoglu19, theorem 2.4] arguing as in [Reference Dal Maso and Modica12].
Acknowledgements
The work of FS was partially supported by the project Variational methods for stationary and evolution problems with singularities and interfaces PRIN 2017 (2017BTM7SN) financed by the Italian Ministry of Education, University, and Research and by the project Starplus 2020 Unina Linea 1 New challenges in the variational modelling of continuum mechanics from the University of Naples ‘Federico II’ and Compagnia di San Paolo (CUP: E65F20001630003). He is also member of the GNAMPA group of INdAM. The work of RM was supported by the German Science Foundation DFG in context of the Emmy Noether Junior Research Group BE 5922/1-1.
Appendix A. A remark on the non-local approximation of free-discontinuity problems in $GSBV$
This Appendix is devoted to the statement of a $\Gamma$![]() -convergence Theorem for non-local functionals depending on the full deformation gradient $\nabla u$
-convergence Theorem for non-local functionals depending on the full deformation gradient $\nabla u$![]() . The result we are going to state has actually been proved in [Reference Cortesani9, theorem 3.2], under an additional technical assumption, the so-called stable $\gamma$
. The result we are going to state has actually been proved in [Reference Cortesani9, theorem 3.2], under an additional technical assumption, the so-called stable $\gamma$![]() -convergence of the functionals
-convergence of the functionals

This assumption, stated in [Reference Cortesani9, definition 7.2] is stronger than simple $\Gamma$![]() -convergence, and introduces a limitation to the class of functionals to which the theorem applies, although relevant examples fulfilling this condition can be readily provided (see [Reference Cortesani9, Examples 7.3–7.5]). Actually, the inspection of the proof of proposition 5.1, which can be clearly adapted to the $GSBV$
-convergence, and introduces a limitation to the class of functionals to which the theorem applies, although relevant examples fulfilling this condition can be readily provided (see [Reference Cortesani9, Examples 7.3–7.5]). Actually, the inspection of the proof of proposition 5.1, which can be clearly adapted to the $GSBV$![]() setting, shows that it is not needed. For the reader's convenience we give a precise statement of the result, after recalling the structural assumptions on the non-local approximation energies under which it is formulated.
setting, shows that it is not needed. For the reader's convenience we give a precise statement of the result, after recalling the structural assumptions on the non-local approximation energies under which it is formulated.
The functions $W_k$![]() are assumed to satisfy ($W1$
are assumed to satisfy ($W1$![]() )–($W2$
)–($W2$![]() ), together with
), together with
(W4′) for every $x\in \mathbb {R}^n$
 and every $M\in \mathbb {M}^{n\times n}$
and every $M\in \mathbb {M}^{n\times n}$ \[ c_1|M|^p\le W_k(x,M)\le c_2(|M|^p+1)\,. \]
\[ c_1|M|^p\le W_k(x,M)\le c_2(|M|^p+1)\,. \]
We will denote with $\widetilde E$![]() the $\Gamma$
the $\Gamma$![]() -limit with respect to the convergence in measure of the functionals $\widetilde E_k$
-limit with respect to the convergence in measure of the functionals $\widetilde E_k$![]() in (A.1), given by (see [Reference Dal Maso14, theorem 20.4])
in (A.1), given by (see [Reference Dal Maso14, theorem 20.4])

where, for every $x\in u$![]() and every $M\in \mathbb {M}^{n\times n}$
and every $M\in \mathbb {M}^{n\times n}$![]()
Above, $W'$![]() and $W''$
and $W''$![]() are defined in (2.7), and (2.8), respectively, provided that $E_k$
are defined in (2.7), and (2.8), respectively, provided that $E_k$![]() is replaced by $\widetilde E_k$
is replaced by $\widetilde E_k$![]() . We then consider the non-local functionals
. We then consider the non-local functionals

where $\rho _k$![]() are as in § 2.3, while $f_k\colon [0, +\infty )\to [0, +\infty )$
are as in § 2.3, while $f_k\colon [0, +\infty )\to [0, +\infty )$![]() are concave and satisfy
are concave and satisfy
for suitable uniform constants $a_1$![]() , $b_1$
, $b_1$![]() , $b_2 >0$
, $b_2 >0$![]() . We then have the following theorem.
. We then have the following theorem.
Theorem A.1 Assume ($W1$![]() ), ($W2$
), ($W2$![]() ), and $(W4^\prime )$
), and $(W4^\prime )$![]() . Consider a sequence of concave functions $f_k$
. Consider a sequence of concave functions $f_k$![]() as in (A.5) and convolution kernels $\rho _k$
as in (A.5) and convolution kernels $\rho _k$![]() as in § 2.3. Let the functionals $\widetilde F_k$
as in § 2.3. Let the functionals $\widetilde F_k$![]() be given by (A.3). Finally, assume that
be given by (A.3). Finally, assume that
Then $\widetilde F_k$![]() $\Gamma$
$\Gamma$![]() -converge, with respect to the convergence in measure, to a functional of the form
-converge, with respect to the convergence in measure, to a functional of the form
where $W$![]() is given by (A.2), $\alpha =\liminf f_k^\prime (0)$
is given by (A.2), $\alpha =\liminf f_k^\prime (0)$![]() , and $\varphi$
, and $\varphi$![]() is a suitable Carathéodory integrand.
is a suitable Carathéodory integrand.
Proof. By [Reference Cortesani9, theorem 3.1], we have that the $\Gamma$![]() -limit of $\widetilde F_k$
-limit of $\widetilde F_k$![]() is an integral functional of the form
is an integral functional of the form
For $W'$![]() and $W''$
and $W''$![]() as in (2.7), and (2.8), respectively, one has only to show that $W_\infty \le \alpha W''$
as in (2.7), and (2.8), respectively, one has only to show that $W_\infty \le \alpha W''$![]() and $W_\infty \ge \alpha W'$
and $W_\infty \ge \alpha W'$![]() . The first inequality is actually already proved in [Reference Cortesani9, proposition 7.1]. As for the second, notice under assumption (A.5) and taking into account remark 5.2, it can be recovered by exactly following the argument of proposition 5.1, provided one is willing to replace each occurrence of $e(u)$
. The first inequality is actually already proved in [Reference Cortesani9, proposition 7.1]. As for the second, notice under assumption (A.5) and taking into account remark 5.2, it can be recovered by exactly following the argument of proposition 5.1, provided one is willing to replace each occurrence of $e(u)$![]() with $\nabla u$
with $\nabla u$![]() .
.