Hostname: page-component-6bf8c574d5-7jkgd Total loading time: 0 Render date: 2025-02-26T07:40:09.289Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-bifurcation of critical periods from semi-hyperbolic polycycles of quadratic centres

Part of: Qualitative theory

Published online by Cambridge University Press:  01 December 2021

D. Marín ,
M. Saavedra  and
J. Villadelprat
D. Marín
Affiliation:
Departament de Matemàtiques, Edifici Cc, Universitat Autònoma de Barcelona, 08193, Cerdanyola del Vallès, Barcelona, Spain ([email protected]) Centre de Recerca Matemàtica, Edifici Cc, Campus de Bellaterra, 08193, Cerdanyola del Vallès, Barcelona, Spain
M. Saavedra
Affiliation:
Departamento de Matemática, Facultad de Ciencias Físicas y Matemáticas, Universidad de Concepción, Barrio Universitario, Concepción, Casilla 160-C, Chile ([email protected])
J. Villadelprat
Affiliation:
Departament d'Enginyeria Informàtica i Matemàtiques, ETSE, Universitat Rovira i Virgili, 43007 Tarragona, Spain ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we consider the unfolding of saddle-node

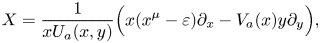
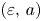\[ X= \frac{1}{xU_a(x,y)}\Big(x(x^{\mu}-\varepsilon)\partial_x-V_a(x)y\partial_y\Big), \]
parametrized by $(\varepsilon,\,a)$ with $\varepsilon \approx 0$ 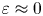and $a$ 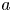in an open subset $A$ 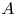of $ {\mathbb {R}}^{\alpha },$ 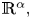and we study the Dulac time $\mathcal {T}(s;\varepsilon,\,a)$ 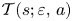of one of its hyperbolic sectors. We prove (theorem 1.1) that the derivative $\partial _s\mathcal {T}(s;\varepsilon,\,a)$ 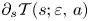tends to $-\infty$ 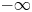as $(s,\,\varepsilon )\to (0^{+},\,0)$ 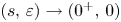uniformly on compact subsets of $A.$ 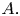This result is addressed to study the bifurcation of critical periods in the Loud's family of quadratic centres. In this regard we show (theorem 1.2) that no bifurcation occurs from certain semi-hyperbolic polycycles.

Keywords

Period functionsaddle-node unfoldingDulac timeasymptotic expansions

MSC classification

Primary: 34C07: Theory of limit cycles of polynomial and analytic vector fields (existence, uniqueness, bounds, Hilbert's 16th problem and ramifications)
Secondary: 34C20: Transformation and reduction of equations and systems, normal forms 34C23: Bifurcation
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 153 , Issue 1 , February 2023 , pp. 104 - 114
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Chicone, C.. The monotonicity of the period function for planar Hamiltonian vector fields. J. Differ. Equ. 69 (1987), 310–321.CrossRefGoogle Scholar
Chicone, C. and Jacobs, M.. Bifurcation of critical periods for plane vector fields. Trans. Amer. Math. Soc. 312 (1989), 433–486.CrossRefGoogle Scholar
Chicone, C., review in MathSciNet, ref. 94h:58072.Google Scholar
Christopher, C. and Devlin, J.. On the classification of Liénard systems with amplitude-independent periods. J. Differ. Equ. 200 (2004), 1–17.CrossRefGoogle Scholar
Cima, A., Ma-osas, F. and Villadelprat, J.. Isochronicity for several classes of Hamiltonian systems. J. Differ. Equ. 157 (1999), 373–413.CrossRefGoogle Scholar
Coppel, W. A. and Gavrilov, L.. The period function of a Hamiltonian quadratic system. Differ. Integr. Equ. 6 (1993), 1357–1365.Google Scholar
Dumortier, F., Llibre, J. and Artés, J. C., Qualitative theory of planar differential systems, Universitext (Springer-Verlag, Berlin, 2006).Google Scholar
Fonda, A., Sabatini, M. and Zanolin, F.. Periodic solutions of perturbed Hamiltonian systems in the plane by the use of the Poincaré-Birkhoff Theorem. Topol. Methods Nonlinear Anal. 40 (2012), 29–52.Google Scholar
Françoise, J.-P. and Pugh, C.. Keeping track of limit cycles. J. Differ. Equ. 65 (1986), 139–157.CrossRefGoogle Scholar
Gasull, A., Guillamon, A. and Villadelprat, J.. The period function for second-order quadratic ODEs is monotone. Qual. Theory Dyn. Syst. 4 (2004), 329–352.CrossRefGoogle Scholar
Gasull, A., Ma-osa, V. and Ma-osas, F.. Stability of certain planar unbounded polycycles. J. Math. Anal. Appl. 269 (2002), 332–351.CrossRefGoogle Scholar
Gasull, A., Liu, C. and Yang, J.. On the number of critical periods for planar polynomial systems of arbitrary degree. J. Differ. Equ. 249 (2010), 684–692.CrossRefGoogle Scholar
Grau, M. and Villadelprat, J.. Bifurcation of critical periods from Pleshkan's isochrones. J. London Math. Soc. 81 (2010), 142–160.CrossRefGoogle Scholar
Greuel, G.-M., Lossen, C. and Shustin, E., Introduction to singularities and deformations, Springer Monogr. Math. (Springer, Berlin, 2007).Google Scholar
Guckenheimer, J. and Holmes, P., Nonlinear oscillations, dynamical systems, and bifurcations of vector fields, Appl. Math. Sci. Vol. 42 (Springer-Verlag, New York, 1983).CrossRefGoogle Scholar
Krantz, S. G. and Parks, H. R., A Primer of Real Analytic Functions, Birkhäuser Advanced Texts (Birkhäuser, Basel, 2002).CrossRefGoogle Scholar
Mardešić, P., Marín, D. and Villadelprat, J.. On the time function of the Dulac map for families of meromorphic vector fields. Nonlinearity 16 (2003), 855–881.CrossRefGoogle Scholar
Mardešić, P., Marín, D. and Villadelprat, J.. The period function of reversible quadratic centers. J. Differ. Equ. 224 (2006), 120–171.CrossRefGoogle Scholar
Mardešić, P., Marín, D. and Villadelprat, J.. Unfolding of resonant saddles and the Dulac time. Discrete Contin. Dyn. Syst. 21 (2008), 1221–1244.CrossRefGoogle Scholar
Mardešić, P., Marín, D., Saavedra, M. and Villadelprat, J.. Unfoldings of saddle-nodes and their Dulac time. J. Differ. Equ. 261 (2016), 6411–6436.CrossRefGoogle Scholar
Marín, D. and Villadelprat, J.. On the return time function around monodromic polycycles. J. Differ. Equ. 228 (2006), 226–258.CrossRefGoogle Scholar
Roussarie, R., Bifurcation of planar vector fields and Hilbert's sixteenth problem, Progr. Math. Vol. 164 (Birkhüser Verlag, Basel, 1998).CrossRefGoogle Scholar
Saavedra, M.. Dulac time of a resonant saddle in the Loud family. J. Differ. Equ. 269 (2020), 7705–7729.CrossRefGoogle Scholar
Villadelprat, J.. On the reversible quadratic centers with monotonic period function. Proc. Amer. Math. Soc. 135 (2007), 2555–2565.CrossRefGoogle Scholar
Xingwu, C. and Zhang, W.. Isochronicity of centers in a switching Bautin system. J. Differ. Equ. 252 (2012), 2877–2899.Google Scholar
Ye, Yan-Qian, et al. , Theory of limit cycles, Transl. Math. Monogr. Vol. 66 (American Mathematical Society, Providence, RI, 1986).Google Scholar
Zhao, Y.. On the monotonicity of the period function of a quadratic system. Discrete Contin. Dyn. Syst. 13 (2005), 795–810.CrossRefGoogle Scholar