Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-01-14T12:09:57.599Z Has data issue: false hasContentIssue false
  • English
  • Français

Necessary and sufficient conditions for asymptotic decay of oscillations in delayed functional equations†

Published online by Cambridge University Press:  14 November 2011

Lu-San Chen  and
Cheh-Chih Yeh
Lu-San Chen
Affiliation:
Institute of Mathematics, National Central University, Chung-Li, Taiwan and Institute ofMathematics, Academia Sinica, Taipei, Taiwan
Cheh-Chih Yeh
Affiliation:
Department of Mathematics, National Central University, Chung-Li, Taiwan
Get access Rights & Permissions [Opens in a new window]

Synopsis

This paper studies the equation

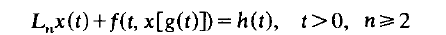
where the differential operator Ln is defined by

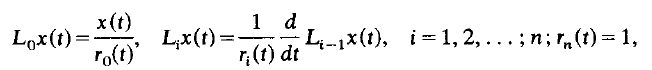
and a necessary and sufficient condition that all oscillatory solutions of the above equation converge to zero asymptotically is presented. The results obtained extend and improve previous ones of Kusano and Onose, and Singh, even in the usual case where

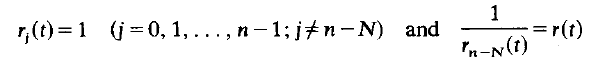
where N is an integer with l≦N≦n–1.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 91 , Issue 1-2 , 1981 , pp. 135 - 145
Copyright
Copyright © Royal Society of Edinburgh 1981

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Chen, Lu-San. On the oscillation and asymptotic properties for general non-linear differential equations. Rend. Accad. Naz. Lincei 61 (1976), 211–216.Google Scholar
2Chen, Lu-San. A Lyapunov inequality and forced oscillations in general non-linear n-th order differential-difference equations. Glasgow Math. J. 18 (1977), 161–166.CrossRefGoogle Scholar
3Chen, Lu-San, Yeh, Cheh-Chih and Lin, Jinn-Tyah. Asymptotic behavior of solutions of functional n-th order differential equations. Bull. London Math. Soc. 10 (1978), 186–190.CrossRefGoogle Scholar
4Chiou, K. L.. Oscillation and non-oscillation theorems for second order functional differential equations. J. Math. Anal. Appl. 45 (1974), 382–403.CrossRefGoogle Scholar
5Kartsatos, A. G.. Maintenance of oscillations under the effect of a periodic forcing term. Proc. Amer. Math. Soc. 33 (1972), 377–383.CrossRefGoogle Scholar
6Kusano, T. and Onose, H.. Asymptotic decay of oscillatory solutions of second order differential equation with forcing term. Proc. Amer. Math. Soc. 2 (1977), 251–257.CrossRefGoogle Scholar
7Singh, B.. Necessary and sufficient condition for eventual decay of oscillations in general functional equations with delays. Hiroshima Math. J. 10 (1980), 1–9.CrossRefGoogle Scholar