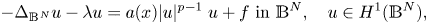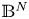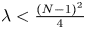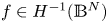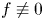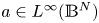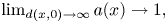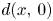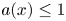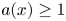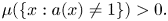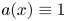1. Introduction
In this paper, we aim to study the existence, multiplicity, and asymptotic estimates of solutions to the following elliptic problem on the hyperbolic space $\mathbb {B}^{N}$![]()

where $1< p<2^*-1:=\frac {N+2}{N-2}$![]() , if $N \geqslant 3; 1< p<+\infty$
, if $N \geqslant 3; 1< p<+\infty$![]() , if $N = 2,\,\;\lambda < \frac {(N-1)^2}{4},$
, if $N = 2,\,\;\lambda < \frac {(N-1)^2}{4},$![]() $H^{1}(\mathbb {B}^{N})$
$H^{1}(\mathbb {B}^{N})$![]() denotes the Sobolev space on the disc model of the hyperbolic space $\mathbb {B}^{N},$
denotes the Sobolev space on the disc model of the hyperbolic space $\mathbb {B}^{N},$![]() $\Delta _{\mathbb {B}^{N}}$
$\Delta _{\mathbb {B}^{N}}$![]() denotes the Laplace–Beltrami operator on $\mathbb {B}^{N},$
denotes the Laplace–Beltrami operator on $\mathbb {B}^{N},$![]() $\frac {(N-1)^2}{4}$
$\frac {(N-1)^2}{4}$![]() being the bottom of the $L^2-$
being the bottom of the $L^2-$![]() spectrum of $-\Delta _{\mathbb {B}^{N}},$
spectrum of $-\Delta _{\mathbb {B}^{N}},$![]() and $a(x) \in L^{\infty }(\mathbb {B}^{N}).$
and $a(x) \in L^{\infty }(\mathbb {B}^{N}).$![]() Further, $0< a \in L^{\infty }(\mathbb {B}^{N}),$
Further, $0< a \in L^{\infty }(\mathbb {B}^{N}),$![]() and $0 \not \equiv f \in H^{-1}(\mathbb {B}^{N})$
and $0 \not \equiv f \in H^{-1}(\mathbb {B}^{N})$![]() is a non-negative functional i.e., $f(u) \geq 0$
is a non-negative functional i.e., $f(u) \geq 0$![]() whenever $u \geq 0$
whenever $u \geq 0$![]() . Let us postpone the discussion on the technical assumptions of function $a(x)$
. Let us postpone the discussion on the technical assumptions of function $a(x)$![]() for a while.
for a while.
If the hyperbolic space $\mathbb {B}^{N}$![]() is replaced with the Euclidean space $\mathbb {R}^N,$
is replaced with the Euclidean space $\mathbb {R}^N,$![]() i.e., when the equation ($\mathcal {P}$
i.e., when the equation ($\mathcal {P}$![]() ) is posed on $\mathbb {R}^N$
) is posed on $\mathbb {R}^N$![]() with $f \equiv 0,$
with $f \equiv 0,$![]() has been investigated widely in the last few decades, and several seminal results have been obtained, we name a few, e.g., [Reference Bahri and Li4, Reference Bahri. A and Lions5, Reference Berestycki and Lions7, Reference Berestycki and Lions8, Reference Ding and Ni18, Reference Lions24, Reference Lions25], and this list is far from being complete. The difficulty in treating this problem arises because the domain $\mathbb {R}^N$
has been investigated widely in the last few decades, and several seminal results have been obtained, we name a few, e.g., [Reference Bahri and Li4, Reference Bahri. A and Lions5, Reference Berestycki and Lions7, Reference Berestycki and Lions8, Reference Ding and Ni18, Reference Lions24, Reference Lions25], and this list is far from being complete. The difficulty in treating this problem arises because the domain $\mathbb {R}^N$![]() is unbounded, and standard variational methods would fail due to the lack of compactness of Sobolev embedding even in the subcritical regime. So to tackle such issues, several authors have introduced new tools, particularly the papers mentioned above. Firstly, the existence of Ground state is established by using delicate energy estimates and carefully analysing the breaking levels of Palais-Smale sequences (see [Reference Bahri and Li4]); we also refer to [Reference Cerami13] for a comprehensive treatment of the problem in the last thirty years. Then onwards, the question of the multiplicity of solutions came into prominence for slightly modified problems in the Euclidean space $\mathbb {R}^N,$
is unbounded, and standard variational methods would fail due to the lack of compactness of Sobolev embedding even in the subcritical regime. So to tackle such issues, several authors have introduced new tools, particularly the papers mentioned above. Firstly, the existence of Ground state is established by using delicate energy estimates and carefully analysing the breaking levels of Palais-Smale sequences (see [Reference Bahri and Li4]); we also refer to [Reference Cerami13] for a comprehensive treatment of the problem in the last thirty years. Then onwards, the question of the multiplicity of solutions came into prominence for slightly modified problems in the Euclidean space $\mathbb {R}^N,$![]()

where the potential $a(x) \rightarrow a_{\infty } > 0$![]() as $|x| \rightarrow \infty.$
as $|x| \rightarrow \infty.$![]() Under the radially symmetric assumption on $a(x),$
Under the radially symmetric assumption on $a(x),$![]() existence of infinitely many solutions was obtained by Berestycki–Lions in [Reference Berestycki and Lions8]. Moreover, the question is even more interesting when the symmetric assumption on the potential $a(x)$
existence of infinitely many solutions was obtained by Berestycki–Lions in [Reference Berestycki and Lions8]. Moreover, the question is even more interesting when the symmetric assumption on the potential $a(x)$![]() is dropped. However, considerable progress has also been made in the case in which $a(x)$
is dropped. However, considerable progress has also been made in the case in which $a(x)$![]() is not radially symmetric. The existence of infinitely many positive solutions is obtained in [Reference Cerami, Passaseo and Solimini14]. Also, see [Reference Cerami15–Reference Clapp and Weth17, Reference Malchiodi28, Reference Molle, Musso and Passaseo31].
is not radially symmetric. The existence of infinitely many positive solutions is obtained in [Reference Cerami, Passaseo and Solimini14]. Also, see [Reference Cerami15–Reference Clapp and Weth17, Reference Malchiodi28, Reference Molle, Musso and Passaseo31].
Adachi–Tanaka [Reference Adachi and Tanaka2] considered Eq. ($\mathcal {P}$![]() ) in the whole Euclidean space, with $\lambda = -1$
) in the whole Euclidean space, with $\lambda = -1$![]() , and studied the multiplicity results. In fact, the problem ($\mathcal {P}$
, and studied the multiplicity results. In fact, the problem ($\mathcal {P}$![]() ) is considered as a perturbation of the classical scalar field equation. From the mathematical point of view, it is natural to ask whether the problem ($\mathcal {P}$
) is considered as a perturbation of the classical scalar field equation. From the mathematical point of view, it is natural to ask whether the problem ($\mathcal {P}$![]() ) admits a positive solution and if yes, then its multiplicity/uniqueness, i.e., whether the positive solutions are stable after the perturbation of type ($\mathcal {P}$
) admits a positive solution and if yes, then its multiplicity/uniqueness, i.e., whether the positive solutions are stable after the perturbation of type ($\mathcal {P}$![]() ) is studied. These questions were quite comprehensively studied by Adachi–Tanaka [Reference Adachi and Tanaka2]. Also, refer to [Reference Adachi1, Reference Adachi and Tanaka3]. In [Reference Adachi and Tanaka2], the existence of four solutions has been obtained under the hypothesis $({\mathbf {A}_1})$
) is studied. These questions were quite comprehensively studied by Adachi–Tanaka [Reference Adachi and Tanaka2]. Also, refer to [Reference Adachi1, Reference Adachi and Tanaka3]. In [Reference Adachi and Tanaka2], the existence of four solutions has been obtained under the hypothesis $({\mathbf {A}_1})$![]() below. Moreover, in [Reference Cao and Zhou12, Reference Jeanjean22], the existence of two positive solutions is established when the potential $a$
below. Moreover, in [Reference Cao and Zhou12, Reference Jeanjean22], the existence of two positive solutions is established when the potential $a$![]() satisfies $({\mathbf {A}_2})$
satisfies $({\mathbf {A}_2})$![]() , and $f \not \equiv 0$
, and $f \not \equiv 0$![]() (but small). Although, the cases $({\mathbf {A}_1})$
(but small). Although, the cases $({\mathbf {A}_1})$![]() and $({\mathbf {A}_2})$
and $({\mathbf {A}_2})$![]() do not cover the case $a(x) \equiv 1,$
do not cover the case $a(x) \equiv 1,$![]() Zhu treated this case in [Reference Zhu34], where he proved existence of two positive solutions. The papers mentioned above employ topological arguments, like the Lusternik–Schnirelmn (L-S) category and the min–max arguments, to obtain their multiplicity results. But for such arguments to work, precise energy estimates of solutions to the ‘limiting problem’ are required so that we are away from the critical level (breaking level) of the Palais–Smale sequences. By the ‘limiting problem,’ we mean the following problem
Zhu treated this case in [Reference Zhu34], where he proved existence of two positive solutions. The papers mentioned above employ topological arguments, like the Lusternik–Schnirelmn (L-S) category and the min–max arguments, to obtain their multiplicity results. But for such arguments to work, precise energy estimates of solutions to the ‘limiting problem’ are required so that we are away from the critical level (breaking level) of the Palais–Smale sequences. By the ‘limiting problem,’ we mean the following problem
It is well-known that the above problem admits unique radially symmetric solutions $W \in C^{\infty }(\mathbb {R}^N)$![]() up to translations. Furthermore, it satisfies
up to translations. Furthermore, it satisfies
In particular, $W \in L^{p}(\mathbb {R}^N)$![]() for all $p \geq 1.$
for all $p \geq 1.$![]() As described, the energy estimates in the papers mentioned earlier were involved with integrals of $W$
As described, the energy estimates in the papers mentioned earlier were involved with integrals of $W$![]() , and this decay estimate plays a pivotal role in it.
, and this decay estimate plays a pivotal role in it.
Now coming back to our problem ($\mathcal {P}$![]() ) in the hyperbolic space setting, even if it seems that the equation is a generalization of problems in the Euclidean space, it has many fascinating phenomena. Let us start with the seminal result of Sandeep–Mancini [Reference Mancini and Sandeep29], where the author showed the existence/uniqueness of positive solutions to the problem
) in the hyperbolic space setting, even if it seems that the equation is a generalization of problems in the Euclidean space, it has many fascinating phenomena. Let us start with the seminal result of Sandeep–Mancini [Reference Mancini and Sandeep29], where the author showed the existence/uniqueness of positive solutions to the problem
where $\lambda \leq \frac {(N-1)^2}{4},$![]() $1 < p \leq \frac {N+2}{N-2}$
$1 < p \leq \frac {N+2}{N-2}$![]() if $N \geq 3;$
if $N \geq 3;$![]() $1 < p < \infty$
$1 < p < \infty$![]() if $N=2.$
if $N=2.$![]() They established in the subcritical case, i.e., $p > 1$
They established in the subcritical case, i.e., $p > 1$![]() if $N =2$
if $N =2$![]() and $1 < p < 2^{\star } -1$
and $1 < p < 2^{\star } -1$![]() if $N \geq 3,$
if $N \geq 3,$![]() the problem (1.2) has a positive solution if and only if $\lambda < \frac {(N-1)^2}{4}.$
the problem (1.2) has a positive solution if and only if $\lambda < \frac {(N-1)^2}{4}.$![]() These positive solutions are also shown to be radially symmetric with respect to some point and unique up to hyperbolic isometries, except possibly for $N =2$
These positive solutions are also shown to be radially symmetric with respect to some point and unique up to hyperbolic isometries, except possibly for $N =2$![]() and $\lambda > \frac {2(p+1)}{(p+3)^2}.$
and $\lambda > \frac {2(p+1)}{(p+3)^2}.$![]() Furthermore, the radially symmetric solution $\mathcal {V}$
Furthermore, the radially symmetric solution $\mathcal {V}$![]() satisfies the following asymptotic estimates
satisfies the following asymptotic estimates
where $r:= d(x,\, 0)$![]() denotes the geodesic distance (we refer § 2 for more details).
denotes the geodesic distance (we refer § 2 for more details).
It is worth mentioning that when $p = 2^*-1$![]() , and $a(x) \equiv 1,$
, and $a(x) \equiv 1,$![]() (1.2) is a natural generalization of the widely recognized Brezis-Nirenberg problem [Reference Brezis and Nirenberg11] in the hyperbolic space. In turn, it is possible to regard the problem ($\mathcal {P}$
(1.2) is a natural generalization of the widely recognized Brezis-Nirenberg problem [Reference Brezis and Nirenberg11] in the hyperbolic space. In turn, it is possible to regard the problem ($\mathcal {P}$![]() ) addressed in this article as an extension of a generalized version of the Brezis-Nirenberg problem. Moreover, the authors in [Reference Mancini and Sandeep29] discovered that (1.2) naturally arises when studying the Euler-Lagrange equations that correspond to the Hardy–Sobolev-Maz'ya (HSM) inequalities. They derived a sharp Poincaré–Sobolev inequality in the hyperbolic space (2.3) via the HSM inequality [Reference Maz'ja30] involving first-order derivatives. In the recent past, this equivalence has sparked the curiosity of mathematicians to explore analogous HSM inequalities for higher-order derivatives (see [Reference Lu and Yang26, Reference Lu and Yang27]). The authors in [Reference Li, Lu and Yan23] have thereafter studied the existence, nonexistence, and symmetry of solutions to the higher-order Brezis–Nirenberg problem in the hyperbolic space. The work of the authors highlighted above relies on highly involved estimations of Green's functions for the kernels of powers of fractional Laplacian and the Helgason–Fourier analysis, as well as the Hardy–Littlewood–Sobolev inequality on the hyperbolic space. Concerning the multiplicity of (1.2), the existence of infinitely many radial sign-changing solutions, compactness, and non-degeneracy was studied in ([Reference Bhakta and Sandeep9, Reference Ganguly and Sandeep19, Reference Ganguly and Sandeep20]). We also refer [Reference Berchio, Ferrero and Grillo6, Reference Bonforte, Gazzola, Grillo and Vazquez10] for existence, asymptotics of non-finite energy solutions. In this article, we are interested in whether the positive solutions still exist under the perturbation of type ($\mathcal {P}$
) addressed in this article as an extension of a generalized version of the Brezis-Nirenberg problem. Moreover, the authors in [Reference Mancini and Sandeep29] discovered that (1.2) naturally arises when studying the Euler-Lagrange equations that correspond to the Hardy–Sobolev-Maz'ya (HSM) inequalities. They derived a sharp Poincaré–Sobolev inequality in the hyperbolic space (2.3) via the HSM inequality [Reference Maz'ja30] involving first-order derivatives. In the recent past, this equivalence has sparked the curiosity of mathematicians to explore analogous HSM inequalities for higher-order derivatives (see [Reference Lu and Yang26, Reference Lu and Yang27]). The authors in [Reference Li, Lu and Yan23] have thereafter studied the existence, nonexistence, and symmetry of solutions to the higher-order Brezis–Nirenberg problem in the hyperbolic space. The work of the authors highlighted above relies on highly involved estimations of Green's functions for the kernels of powers of fractional Laplacian and the Helgason–Fourier analysis, as well as the Hardy–Littlewood–Sobolev inequality on the hyperbolic space. Concerning the multiplicity of (1.2), the existence of infinitely many radial sign-changing solutions, compactness, and non-degeneracy was studied in ([Reference Bhakta and Sandeep9, Reference Ganguly and Sandeep19, Reference Ganguly and Sandeep20]). We also refer [Reference Berchio, Ferrero and Grillo6, Reference Bonforte, Gazzola, Grillo and Vazquez10] for existence, asymptotics of non-finite energy solutions. In this article, we are interested in whether the positive solutions still exist under the perturbation of type ($\mathcal {P}$![]() ). If it exists, then study its asymptotic estimates and multiplicity. In our previous article [Reference Ganguly, Gupta and Sreenadh21], we showed the existence of a positive solution with high energy when $f \equiv 0.$
). If it exists, then study its asymptotic estimates and multiplicity. In our previous article [Reference Ganguly, Gupta and Sreenadh21], we showed the existence of a positive solution with high energy when $f \equiv 0.$![]() Here we considered a multiplicity of solutions along the lines of previous authors. As one anticipates, we follow the topological /variational arguments to obtain multiple solutions. Still, the major hurdle lies in the energy estimates involving solutions to (1.2) since one could see easily that $\mathcal {V} \notin L^{p}(\mathbb {B}^{N})$
Here we considered a multiplicity of solutions along the lines of previous authors. As one anticipates, we follow the topological /variational arguments to obtain multiple solutions. Still, the major hurdle lies in the energy estimates involving solutions to (1.2) since one could see easily that $\mathcal {V} \notin L^{p}(\mathbb {B}^{N})$![]() for $p \in [1,\,2) .$
for $p \in [1,\,2) .$![]() This step is quite delicately handled in § 6. Moreover, we also studied asymptotic estimates of solutions to ($\mathcal{P}$
This step is quite delicately handled in § 6. Moreover, we also studied asymptotic estimates of solutions to ($\mathcal{P}$![]() ) for $a(x) \equiv 1$
) for $a(x) \equiv 1$![]() and $f$
and $f$![]() satisfies some decay estimates. Indeed the ode approach won't work in this case, as apriori $f$
satisfies some decay estimates. Indeed the ode approach won't work in this case, as apriori $f$![]() is not given to be a radial function, and hence we tackle this problem using the barrier argument (See § 5).
is not given to be a radial function, and hence we tackle this problem using the barrier argument (See § 5).
Now let us describe all the necessary assumptions before stating our main theorems. We investigate the solutions of ($\mathcal {P}$![]() ) under the following cases separately:
) under the following cases separately:

Further, let us prescribe an assumption on the parameter $\lambda :$![]()

We are now in a position to state this article's main theorems. Let us begin with the Adachi–Tanaka [Reference Adachi and Tanaka2] type result in the hyperbolic space setting :
Theorem 1.1 Let $a \in C(\mathbb {B}^{N})$![]() satisfies $(\mathbf {A}_{1}).$
satisfies $(\mathbf {A}_{1}).$![]() In addition, assume that $a$
In addition, assume that $a$![]() also satisfies
also satisfies
for some positive constants $C$![]() and $\delta.$
and $\delta.$![]() Then there exists $\delta _{0}>0$
Then there exists $\delta _{0}>0$![]() such that the equation ($\mathcal {P}$
such that the equation ($\mathcal {P}$![]() ) has at least three positive solutions for any non-negative $f \in H^{-1}(\mathbb {B}^{N})$
) has at least three positive solutions for any non-negative $f \in H^{-1}(\mathbb {B}^{N})$![]() with $\|f\|_{H^{-1}(\mathbb {B}^{N})} \leq \delta _{0}$
with $\|f\|_{H^{-1}(\mathbb {B}^{N})} \leq \delta _{0}$![]() and for $\lambda$
and for $\lambda$![]() satisfying (1.3).
satisfying (1.3).
Remark 1.2 In contrast with Adachi–Tanaka [Reference Adachi and Tanaka2], here we obtain the existence of at least three solutions instead of four. This is purely a technical reason for not getting the fourth solution, which can be attributed to the new energy estimates phenomenon in the hyperbolic space.
Next, we assume $a(x) \geq 1,$![]() and we prove the following result :
and we prove the following result :
Theorem 1.3 Let $a$![]() satisfies $(\mathbf {A}_{2}),\, 0 \not \equiv f \in H^{-1}(\mathbb {B}^{N})$
satisfies $(\mathbf {A}_{2}),\, 0 \not \equiv f \in H^{-1}(\mathbb {B}^{N})$![]() is a non-negative functional and $S_{1,\lambda }$
is a non-negative functional and $S_{1,\lambda }$![]() be defined as in (3.10). Furthermore, if
be defined as in (3.10). Furthermore, if
Then ($\mathcal {P}$![]() ) admits at least two positive solutions for $\lambda$
) admits at least two positive solutions for $\lambda$![]() satisfying (1.3).
satisfying (1.3).
Further, if $a$![]() satisfies $(\mathbf {A}_{3})$
satisfies $(\mathbf {A}_{3})$![]() , i.e., ($\mathcal {P}$
, i.e., ($\mathcal {P}$![]() ) becomes the following
) becomes the following

where all the notations are the same as for the problem ($\mathcal {P}$![]() ) then we have the following theorem.
) then we have the following theorem.
Theorem 1.4 Assume that $a$![]() satisfies $(\mathbf {A}_{3})$
satisfies $(\mathbf {A}_{3})$![]() . Then there exists $\delta _{0}^{'}>0$
. Then there exists $\delta _{0}^{'}>0$![]() such that the problem (𝒫′) has at least two positive solutions any non-negative $f \in H^{-1}(\mathbb {B}^{N})$
such that the problem (𝒫′) has at least two positive solutions any non-negative $f \in H^{-1}(\mathbb {B}^{N})$![]() with $\|f\|_{H^{-1}(\mathbb {B}^{N})} \leq \delta _{0}^{'}$
with $\|f\|_{H^{-1}(\mathbb {B}^{N})} \leq \delta _{0}^{'}$![]() and for $\lambda$
and for $\lambda$![]() satisfying (1.3).
satisfying (1.3).
The paper is organized as follows: In § 2, we introduce some of the notations, geometric definitions, and preliminaries concerning the hyperbolic space. Section 3 describes the energy functional, setting up the problem, and associated auxiliary lemmas involving functionals. In § 4, we state and prove the Palais-Smale decomposition theorem as Proposition 4.1 and 4.2. Whereas in § 5, we obtain asymptotic estimates for the solution of (𝒫′) S 6 is devoted to the key energy estimates involving the solutions of (1.2). The proof of Theorem 1.1 and Theorem 1.3 are given in § 7. Finally, § 8 is devoted to the proof of Theorem 1.4.
2. Preliminaries
In this section, we will introduce some of the notations and definitions used in this paper and also recall some of the embeddings related to the Sobolev space on the hyperbolic space. We will denote by $\mathbb {B}^{N}$![]() the disc model of the hyperbolic space, i.e., the unit disc equipped with the Riemannian metric $g_{\mathbb {B}^{N}} := \sum _{i=1}^N (\frac {2}{1-|x|^2})^2 \, \textrm {d}x_i^2$
the disc model of the hyperbolic space, i.e., the unit disc equipped with the Riemannian metric $g_{\mathbb {B}^{N}} := \sum _{i=1}^N (\frac {2}{1-|x|^2})^2 \, \textrm {d}x_i^2$![]() . To simplify our notations, we will denote $g_{\mathbb {B}^{N}}$
. To simplify our notations, we will denote $g_{\mathbb {B}^{N}}$![]() by $g$
by $g$![]() . The corresponding volume element is given by $\mathrm {~d} V_{\mathbb {B}^{N}} = (\frac {2}{1-|x|^2})^N \textrm {d}x,\,$
. The corresponding volume element is given by $\mathrm {~d} V_{\mathbb {B}^{N}} = (\frac {2}{1-|x|^2})^N \textrm {d}x,\,$![]() where $\textrm {d}x$
where $\textrm {d}x$![]() denotes the Lebesgue measure on $\mathbb {R}^{N}$
denotes the Lebesgue measure on $\mathbb {R}^{N}$![]() . Hyperbolic distance on $\mathbb {B}^{N}$
. Hyperbolic distance on $\mathbb {B}^{N}$![]() . The hyperbolic distance between two points $x$
. The hyperbolic distance between two points $x$![]() and $y$
and $y$![]() in $\mathbb {B}^{N}$
in $\mathbb {B}^{N}$![]() will be denoted by $d(x,\, y).$
will be denoted by $d(x,\, y).$![]() For the hyperbolic distance between $x$
For the hyperbolic distance between $x$![]() and the origin we write
and the origin we write
where $r = |x|$![]() , which in turn implies that $r = \tanh \frac {\rho }{2}.$
, which in turn implies that $r = \tanh \frac {\rho }{2}.$![]() Moreover, the hyperbolic distance between $x,\, y \in \mathbb {B}^{N}$
Moreover, the hyperbolic distance between $x,\, y \in \mathbb {B}^{N}$![]() is given by
is given by
It easily follows that a subset $S$![]() of $\mathbb {B}^{N}$
of $\mathbb {B}^{N}$![]() is a hyperbolic sphere in $\mathbb {B}^{N}$
is a hyperbolic sphere in $\mathbb {B}^{N}$![]() if and only if $S$
if and only if $S$![]() is a Euclidean sphere in $\mathbb {R}^N$
is a Euclidean sphere in $\mathbb {R}^N$![]() and contained in $\mathbb {B}^{N}$
and contained in $\mathbb {B}^{N}$![]() , probably with a different centre and different radius, which can be computed. Geodesic balls in $\mathbb {B}^{N}$
, probably with a different centre and different radius, which can be computed. Geodesic balls in $\mathbb {B}^{N}$![]() of radius $a$
of radius $a$![]() centred at the origin will be denoted by
centred at the origin will be denoted by
We also need some information on the isometries of $\mathbb {B}^{N}$![]() . Below we recall the definition of a particular type of isometry, namely the hyperbolic translation. For more details on the isometry group of $\mathbb {B}^{N}$
. Below we recall the definition of a particular type of isometry, namely the hyperbolic translation. For more details on the isometry group of $\mathbb {B}^{N}$![]() , we refer to [Reference Ratcliffe32].
, we refer to [Reference Ratcliffe32].
Hyperbolic translation. For $b \in \mathbb {B}^{N},$![]() define
define
then $\tau _b$![]() is an isometry of $\mathbb {B}^{N}$
is an isometry of $\mathbb {B}^{N}$![]() with $\tau _b(0) = b.$
with $\tau _b(0) = b.$![]() The map $\tau _b$
The map $\tau _b$![]() is called the hyperbolic translation of $\mathbb {B}^{N}$
is called the hyperbolic translation of $\mathbb {B}^{N}$![]() by $b.$
by $b.$![]() It can also be seen that $\tau _{-b} = \tau _b^{-1}.$
It can also be seen that $\tau _{-b} = \tau _b^{-1}.$![]()
The hyperbolic gradient $\nabla _{\mathbb {B}^{N}}$![]() and the hyperbolic Laplacian $\Delta _{\mathbb {B}^{N}}$
and the hyperbolic Laplacian $\Delta _{\mathbb {B}^{N}}$![]() are given by
are given by

Laplace–Beltrami operator on $\mathbb {B}^{N}$![]() . It is well known that the $N$
. It is well known that the $N$![]() -dimensional hyperbolic space $\mathbb {B}^{N}$
-dimensional hyperbolic space $\mathbb {B}^{N}$![]() admits a polar coordinate decomposition structure. Namely, for $x\in \mathbb {B}^{N}$
admits a polar coordinate decomposition structure. Namely, for $x\in \mathbb {B}^{N}$![]() we can write $x=(r,\, \Theta )=(r,\, \theta _{1},\,\ldots,\, \theta _{N-1})\in (0,\,\infty )\times \mathbb {S}^{N-1}$
we can write $x=(r,\, \Theta )=(r,\, \theta _{1},\,\ldots,\, \theta _{N-1})\in (0,\,\infty )\times \mathbb {S}^{N-1}$![]() , where $r$
, where $r$![]() denotes the geodesic distance between the point $x$
denotes the geodesic distance between the point $x$![]() and a fixed pole $0$
and a fixed pole $0$![]() in $\mathbb {B}^{N}$
in $\mathbb {B}^{N}$![]() and $\mathbb {S}^{N-1}$
and $\mathbb {S}^{N-1}$![]() is the unit sphere in the $N$
is the unit sphere in the $N$![]() -dimensional euclidean space $\mathbb {R}^N$
-dimensional euclidean space $\mathbb {R}^N$![]() . Recall that the Riemannian Laplacian of a scalar function $u$
. Recall that the Riemannian Laplacian of a scalar function $u$![]() on $\mathbb {B}^{N}$
on $\mathbb {B}^{N}$![]() is given by
is given by
where $\Delta _{\mathbb {S}^{N-1}}$![]() is the Riemannian Laplacian on the unit sphere $\mathbb {S}^{N-1}$
is the Riemannian Laplacian on the unit sphere $\mathbb {S}^{N-1}$![]() .
.
A sharp Poincaré-Sobolev inequality. (see [Reference Mancini and Sandeep29])
We will denote by ${H^{1}}(\mathbb {B}^{N})$![]() the Sobolev space on the disc model of the hyperbolic space $\mathbb {B}^{N}$
the Sobolev space on the disc model of the hyperbolic space $\mathbb {B}^{N}$![]() , equipped with norm $\|u\|=(\int _{\mathbb {B}^N} |\nabla _{\mathbb {B}^{N}} u|^{2})^{\frac {1}{2}},$
, equipped with norm $\|u\|=(\int _{\mathbb {B}^N} |\nabla _{\mathbb {B}^{N}} u|^{2})^{\frac {1}{2}},$![]() where $|\nabla _{\mathbb {B}^{N}} u|$
where $|\nabla _{\mathbb {B}^{N}} u|$![]() is given by $|\nabla _{\mathbb {B}^{N}} u| := \langle \nabla _{\mathbb {B}^{N}} u,\, \nabla _{\mathbb {B}^{N}} u \rangle ^{\frac {1}{2}}_{\mathbb {B}^{N}} .$
is given by $|\nabla _{\mathbb {B}^{N}} u| := \langle \nabla _{\mathbb {B}^{N}} u,\, \nabla _{\mathbb {B}^{N}} u \rangle ^{\frac {1}{2}}_{\mathbb {B}^{N}} .$![]()
For $N \geq 3$![]() and every $p \in (1,\, \frac {N+2}{N-2} ]$
and every $p \in (1,\, \frac {N+2}{N-2} ]$![]() there exists an optimal constant $S_{N,p} > 0$
there exists an optimal constant $S_{N,p} > 0$![]() such that
such that

for every $u \in C^{\infty }_{0}(\mathbb {B}^{N}).$![]() If $N = 2$
If $N = 2$![]() , then any $p > 1$
, then any $p > 1$![]() is allowed.
is allowed.
A basic information is that the bottom of the spectrum of $- \Delta _{\mathbb {B}^{N}}$![]() on $\mathbb {B}^{N}$
on $\mathbb {B}^{N}$![]() is
is
Remark 2.1 A consequence of (2.4) is that if $\lambda < \frac {(N-1)^2}{4},$![]() then
then

is a norm, equivalent to the $H^1(\mathbb {B}^{N})$![]() norm and the corresponding inner product is given by $\langle u,\, v\rangle _{H_{\lambda }}.$
norm and the corresponding inner product is given by $\langle u,\, v\rangle _{H_{\lambda }}.$![]()
3. Energy functional and preliminary lemmas
3.1. Unperturbed equation
First, let us recall the asymptotic estimates of positive solutions to the following homogeneous problem
Then by elliptic regularity, any solution, $w\in H^1(\mathbb {B}^{N}),$![]() is also in $C^\infty$
is also in $C^\infty$![]() and satisfies the decay property (See [Reference Mancini and Sandeep29, Lemma 3.4]): for every $\varepsilon > 0,$
and satisfies the decay property (See [Reference Mancini and Sandeep29, Lemma 3.4]): for every $\varepsilon > 0,$![]() there exist positive constants $C_1^{\varepsilon }$
there exist positive constants $C_1^{\varepsilon }$![]() and $C_2^{\varepsilon }$
and $C_2^{\varepsilon }$![]() such that there holds
such that there holds
where $c(N,\, \lambda ) = \frac {1}{2} (N-1+\sqrt {(N-1)^{2}-4 \lambda }).$![]()
3.2. Energy functional
For given $a(x)$![]() and $f(x)$
and $f(x)$![]() , we define $I_{\lambda,a, f}(u): H^{1}(\mathbb {B}^{N}) \rightarrow \mathbb {R}$
, we define $I_{\lambda,a, f}(u): H^{1}(\mathbb {B}^{N}) \rightarrow \mathbb {R}$![]() by
by
It is obvious that if $u$![]() is a critical point of $I_{\lambda, a, f}$
is a critical point of $I_{\lambda, a, f}$![]() , then $u$
, then $u$![]() is the solution to the following problem
is the solution to the following problem

Remark 3.1 If we take $v=u_{-}$![]() as a test function in (3.4) where $u$
as a test function in (3.4) where $u$![]() is a weak solution of (3.4) and $f$
is a weak solution of (3.4) and $f$![]() is a non-negative functional, we obtain $u_{-}=0$
is a non-negative functional, we obtain $u_{-}=0$![]() , i.e., $u \geq 0$
, i.e., $u \geq 0$![]() . Thus $u>0$
. Thus $u>0$![]() follows from the maximum principle, and hence $u$
follows from the maximum principle, and hence $u$![]() is a solution to ($\mathcal {P}$
is a solution to ($\mathcal {P}$![]() ).
).
Define
where

In the subsequent sections, we will establish that the positive solutions of ($\mathcal {P}$![]() ) correspond to the critical points of $I_{\lambda, a, f}(u): H^{1}(\mathbb {B}^{N}) \rightarrow \mathbb {R}$
) correspond to the critical points of $I_{\lambda, a, f}(u): H^{1}(\mathbb {B}^{N}) \rightarrow \mathbb {R}$![]() or $J_{\lambda, a, f}(v)$
or $J_{\lambda, a, f}(v)$![]() : $\tilde \Sigma _+ \rightarrow \mathbb {R}$
: $\tilde \Sigma _+ \rightarrow \mathbb {R}$![]() . To this end we set
. To this end we set

Using the definition of $J_{\lambda,a, f},$![]() and carrying out some easy calculations we obtain
and carrying out some easy calculations we obtain

Therefore
Further, since $w$![]() is the unique radial solution of (3.1), we have
is the unique radial solution of (3.1), we have
Moreover,
We define the functionals $J,\, J_\infty : H^1(\mathbb {B}^{N})\rightarrow \mathbb {R}$![]() as
as

and the energy levels
3.3. Auxliary Lemmas
We require the following auxiliary lemmas to prove Theorem 1.1.
The subsequent lemmas give us the inequalities involving $I_{\lambda,a, f}\;(J_{\lambda,a, f})$![]() and $I_{\lambda,a(\varepsilon ),0}\;(J_{\lambda,a(\varepsilon ),0})$
and $I_{\lambda,a(\varepsilon ),0}\;(J_{\lambda,a(\varepsilon ),0})$![]() for $\varepsilon \in (0,\,1).$
for $\varepsilon \in (0,\,1).$![]()
Lemma 3.2
(i) The following inequality holds for $u \in H^{1}(\mathbb {B}^{N})$
 and $\varepsilon \in (0,\,1)$
and $\varepsilon \in (0,\,1)$ (3.11)\begin{align} & (1-\varepsilon) I_{\lambda,\frac{a}{1-\varepsilon}, 0}(u)-\frac{1}{2 \varepsilon}\|f\|_{H^{{-}1}\left(\mathbb{B}^{N}\right)}^{2} \leq I_{\lambda,a, f}(u)\nonumber\\ & \quad \leq(1+\varepsilon) I_{\lambda,\frac{a}{1+\varepsilon}, 0}(u)+\frac{1}{2 \varepsilon}\left\|f\right\|_{H^{{-}1}\left(\mathbb{B}^{N}\right)}^{2} .\end{align}
(3.11)\begin{align} & (1-\varepsilon) I_{\lambda,\frac{a}{1-\varepsilon}, 0}(u)-\frac{1}{2 \varepsilon}\|f\|_{H^{{-}1}\left(\mathbb{B}^{N}\right)}^{2} \leq I_{\lambda,a, f}(u)\nonumber\\ & \quad \leq(1+\varepsilon) I_{\lambda,\frac{a}{1+\varepsilon}, 0}(u)+\frac{1}{2 \varepsilon}\left\|f\right\|_{H^{{-}1}\left(\mathbb{B}^{N}\right)}^{2} .\end{align}
(ii) Suppose $v \in \tilde {\Sigma }_+$
 and $\varepsilon \in (0,\,1)$
and $\varepsilon \in (0,\,1)$ . Then there holds
(3.12)\begin{align} & (1-\varepsilon)^{\frac{p+1}{p-1}} J_{\lambda,a, 0}(v)-\frac{1}{2 \varepsilon}\|f\|_{ H^{{-}1}\left(\mathbb{B}^{N}\right)}^{2} \leq J_{\lambda,a, f}(v)\nonumber\\ & \quad \leq(1+\varepsilon)^{\frac{p+1}{p-1}} J_{\lambda,a, 0}(v)+\frac{1}{2 \varepsilon}\left\|f\right\|_{H^{{-}1}\left(\mathbb{B}^{N}\right)}^{2}. \end{align}
. Then there holds
(3.12)\begin{align} & (1-\varepsilon)^{\frac{p+1}{p-1}} J_{\lambda,a, 0}(v)-\frac{1}{2 \varepsilon}\|f\|_{ H^{{-}1}\left(\mathbb{B}^{N}\right)}^{2} \leq J_{\lambda,a, f}(v)\nonumber\\ & \quad \leq(1+\varepsilon)^{\frac{p+1}{p-1}} J_{\lambda,a, 0}(v)+\frac{1}{2 \varepsilon}\left\|f\right\|_{H^{{-}1}\left(\mathbb{B}^{N}\right)}^{2}. \end{align}
(iii) In particular, there exists $d_{0}>0$
 such that if $\|f\|_{H^{-1}(\mathbb {B}^{N})} \leq d_{0}$
such that if $\|f\|_{H^{-1}(\mathbb {B}^{N})} \leq d_{0}$ , then,
\[ \inf _{v \in \tilde{\Sigma}_+} J_{\lambda,a, f}(v)>0 . \]
, then,
\[ \inf _{v \in \tilde{\Sigma}_+} J_{\lambda,a, f}(v)>0 . \]
In the next lemma, for $v \in \tilde {\Sigma }_+$![]() , we analyse the function $\tilde {g}(t):[0,\, \infty ) \rightarrow \mathbb {R}$
, we analyse the function $\tilde {g}(t):[0,\, \infty ) \rightarrow \mathbb {R}$![]() defined by
defined by
Lemma 3.3
(i) The function $\tilde {g}$
 has at most two critical points in $[0,\, \infty )$
has at most two critical points in $[0,\, \infty )$ for every $v \in \tilde {\Sigma }_+$
for every $v \in \tilde {\Sigma }_+$ .
.(ii) If $\|f\|_{H^{-1}(\mathbb {B}^{N})} \leq d_{0}(d_{0}$
 as chosen in Lemma 3.2), then for any $v \in \tilde {\Sigma }_+$
as chosen in Lemma 3.2), then for any $v \in \tilde {\Sigma }_+$ , there exists a unique $t_{a, f}(v)>0$
, there exists a unique $t_{a, f}(v)>0$ such that $I_{\lambda,a, f}(t_{a, f}(v) v)=J_{\lambda,a, f}(v)$
such that $I_{\lambda,a, f}(t_{a, f}(v) v)=J_{\lambda,a, f}(v)$ , where $J_{\lambda,a, f}$
, where $J_{\lambda,a, f}$ is defined as in (3.6). Moreover, $t_{a, f}(v)>0$
is defined as in (3.6). Moreover, $t_{a, f}(v)>0$ satisfies
(3.13)\begin{equation} t_{a, f}(v)>\left(p \int_{\mathbb{B}^{N}} a(x) v_+^{p+1} \mathrm{~d} V_{\mathbb{B}^{N}}(x)\right)^{-\frac{1}{p-1}} \geq\left(p S_{1,\lambda}^{-\frac{(p+1)}{2}}\right)^{-\frac{1}{p-1}}. \end{equation}Additionally, we also have
satisfies
(3.13)\begin{equation} t_{a, f}(v)>\left(p \int_{\mathbb{B}^{N}} a(x) v_+^{p+1} \mathrm{~d} V_{\mathbb{B}^{N}}(x)\right)^{-\frac{1}{p-1}} \geq\left(p S_{1,\lambda}^{-\frac{(p+1)}{2}}\right)^{-\frac{1}{p-1}}. \end{equation}Additionally, we also have (3.14)\begin{equation} I_{\lambda,a, f}^{\prime \prime}\left(t_{a, f}(v) v\right)(v, v)<0. \end{equation}
(3.14)\begin{equation} I_{\lambda,a, f}^{\prime \prime}\left(t_{a, f}(v) v\right)(v, v)<0. \end{equation}
(iii) Any critical point of $\tilde {g}$
 distinct from $t_{a, f}(v)$
distinct from $t_{a, f}(v)$ lies in $[0,\,(1-\frac {1}{p})^{-1}\|f\|_{H^{-1}(\mathbb {B}^{N})}]$
lies in $[0,\,(1-\frac {1}{p})^{-1}\|f\|_{H^{-1}(\mathbb {B}^{N})}]$ .
.
We omit the details of the proof of the above two lemmas. They can be proved exactly in the spirit of [Reference Adachi and Tanaka2]. The following proposition characterises all the critical points of the functional $I_{\lambda, a, f}$![]() in terms of the functional $J_{\lambda, a, f}$
in terms of the functional $J_{\lambda, a, f}$![]() .
.
Proposition 3.4 Assume $\|f\|_{H^{-1}(\mathbb {B}^{N})} \leq d_{2}$![]() where $d_{2}=\min \left \{d_{1},\,(1-\frac {1}{p}) r_{1}\right \}>0$
where $d_{2}=\min \left \{d_{1},\,(1-\frac {1}{p}) r_{1}\right \}>0$![]() and $d_{1},\, r_{1}$
and $d_{1},\, r_{1}$![]() as chosen in Proposition 7.1. Then the following holds
as chosen in Proposition 7.1. Then the following holds
(i) $J_{\lambda,a, f} \in C^{1}(\tilde {\Sigma }_+,\, \mathbb {R})$
 and
(3.15)\begin{equation} J_{\lambda,a, f}^{\prime}(v) h=t_{a, f}(v) I_{\lambda,a, f}^{\prime}\left(t_{a, f}(v) v\right) h, \end{equation}for all $h \in T_{v} \tilde {\Sigma }_+=\left \{h \in H^{1}(\mathbb {B}^{N}) \mid \langle h,\, v\rangle _{H_{\lambda }}=0\right \}$
and
(3.15)\begin{equation} J_{\lambda,a, f}^{\prime}(v) h=t_{a, f}(v) I_{\lambda,a, f}^{\prime}\left(t_{a, f}(v) v\right) h, \end{equation}for all $h \in T_{v} \tilde {\Sigma }_+=\left \{h \in H^{1}(\mathbb {B}^{N}) \mid \langle h,\, v\rangle _{H_{\lambda }}=0\right \}$
 .
.(ii) $v \in \tilde {\Sigma }_+$
 is a critical point of $J_{\lambda,a, f}(v)$
is a critical point of $J_{\lambda,a, f}(v)$ iff $t_{a, f}(v) v \in H^{1}(\mathbb {B}^{N})$
iff $t_{a, f}(v) v \in H^{1}(\mathbb {B}^{N})$ is a critical point of $I_{\lambda,a, f}(u)$
is a critical point of $I_{\lambda,a, f}(u)$ .
.(iii) In addition, the set containing all the critical points of $I_{\lambda,a, f}(u)$
 can be written as
(3.16)\begin{equation} \left\{t_{a, f}(v) v \mid v \in \tilde{\Sigma}_+, J_{\lambda,a, f}^{\prime}(v)=0\right\} \cup\left\{\mathcal{U}_{a, f} (x)\right\}, \end{equation}where $\mathcal {U}_{a, f}$
can be written as
(3.16)\begin{equation} \left\{t_{a, f}(v) v \mid v \in \tilde{\Sigma}_+, J_{\lambda,a, f}^{\prime}(v)=0\right\} \cup\left\{\mathcal{U}_{a, f} (x)\right\}, \end{equation}where $\mathcal {U}_{a, f}$
 is a critical point of $I_{\lambda, a, f}$
is a critical point of $I_{\lambda, a, f}$ obtained in Proposition 7.1.
obtained in Proposition 7.1.
Proof. We skip the proof for brevity. The proof can be concluded with the necessary modifications for the hyperbolic space. For details, we refer [Reference Adachi and Tanaka2].
4. Palais–Smale Characterization
In this section, we study the Palais–Smale sequences (PS sequences) corresponding to the problem ($\mathcal {P}$![]() ). We say a sequence $u_{n} \in H^{1}(\mathbb {B}^{N})$
). We say a sequence $u_{n} \in H^{1}(\mathbb {B}^{N})$![]() is a Palais-Smale sequence for $I_{\lambda,a,f}$
is a Palais-Smale sequence for $I_{\lambda,a,f}$![]() at a level $d$
at a level $d$![]() if $I_{\lambda,a,f}(u_{n}) \rightarrow d$
if $I_{\lambda,a,f}(u_{n}) \rightarrow d$![]() and $I_{\lambda,a,f}^{\prime }(u_{n}) \rightarrow 0$
and $I_{\lambda,a,f}^{\prime }(u_{n}) \rightarrow 0$![]() in $H^{-1}(\mathbb {B}^{N}) .$
in $H^{-1}(\mathbb {B}^{N}) .$![]() One can easily see that PS sequences are bounded. Throughout this section, we assume $a(x) \rightarrow 1$
One can easily see that PS sequences are bounded. Throughout this section, we assume $a(x) \rightarrow 1$![]() as $d(x,\,0) \rightarrow \infty.$
as $d(x,\,0) \rightarrow \infty.$![]()
In the subsequent propositions, we examine the Palais-Smale condition for $I_{\lambda,a, f}(u)$![]() and $J_{\lambda,a, f}(v)$
and $J_{\lambda,a, f}(v)$![]() . In particular, we prove the following proposition :
. In particular, we prove the following proposition :
Proposition 4.1 Assume $0< a \in L^{\infty }(\mathbb {B}^{N}),\, a(x) \rightarrow 1$![]() as $d(x,\,0) \rightarrow \infty$
as $d(x,\,0) \rightarrow \infty$![]() and $0 \not \equiv f \in H^{-1}(\mathbb {B}^{N})$
and $0 \not \equiv f \in H^{-1}(\mathbb {B}^{N})$![]() is a non-negative functional and suppose that a sequence $\left \{u_{j}\right \}_{j=1}^{\infty } \subset H^{1}(\mathbb {B}^{N})$
is a non-negative functional and suppose that a sequence $\left \{u_{j}\right \}_{j=1}^{\infty } \subset H^{1}(\mathbb {B}^{N})$![]() satisfies
satisfies

as $j \rightarrow \infty$![]() . Then there exists a subsequence—still denoted by $\left \{u_{j}\right \}_{j=1}^{\infty }$
. Then there exists a subsequence—still denoted by $\left \{u_{j}\right \}_{j=1}^{\infty }$![]() , a critical point $u_{0}(x)$
, a critical point $u_{0}(x)$![]() of $I_{\lambda,a, f}(u)$
of $I_{\lambda,a, f}(u)$![]() , an integer $\ell \in \mathbb {N} \cup \{0\}$
, an integer $\ell \in \mathbb {N} \cup \{0\}$![]() , and $\ell$
, and $\ell$![]() sequences of points $\left \{y_{j}^{1}\right \}_{j=1}^{\infty },\, \ldots,\,\left \{y_{j}^{\ell }\right \}_{j=1}^{\infty } \subset \mathbb {B}^{N}$
sequences of points $\left \{y_{j}^{1}\right \}_{j=1}^{\infty },\, \ldots,\,\left \{y_{j}^{\ell }\right \}_{j=1}^{\infty } \subset \mathbb {B}^{N}$![]() such that
such that
(1) $d(y_{j}^{k},\,0) \rightarrow \infty \textrm { as } j \rightarrow \infty \;\;\forall k=1,\,2,\, \ldots,\, \ell,$

(2) $d(y_{j}^{k},\,y_{j}^{k^{\prime }}) \rightarrow \infty \textrm { as } j \rightarrow \infty \textrm { for } k \neq k^{\prime },$

(3) $\left \|u_{j}(x)-(u_{0}(x)+\sum _{k=1}^{\ell } w(\tau _{-y_{j}^{k}}(x)))\right \|_{{H_{\lambda }}} \rightarrow 0$
 as $j \rightarrow \infty$
as $j \rightarrow \infty$ ,
,(4) $I_{\lambda,a, f}(u_{j}) \rightarrow I_{\lambda,a, f}(u_{0})+\ell I_{\lambda,1,0}(w)$
 as $j \rightarrow \infty,$
as $j \rightarrow \infty,$
where $\tau _a,$![]() $a \in \mathbb {B}^{N}$
$a \in \mathbb {B}^{N}$![]() denotes the hyperbolic translation, and $w$
denotes the hyperbolic translation, and $w$![]() is the unique positive radial solution to the unperturbed equation.
is the unique positive radial solution to the unperturbed equation.
Proof. The proof is a straightforward adaption of [Reference Ganguly, Gupta and Sreenadh21, Proposition 3.1] in the case $f \not \equiv 0.$![]() We also refer ([Reference Lions24], [Reference Lions25] and [Reference Struwe33]) for the Euclidean case.
We also refer ([Reference Lions24], [Reference Lions25] and [Reference Struwe33]) for the Euclidean case.
Next, we study the Palais–Smale condition for $J_{\lambda,a,f}.$![]()
Proposition 4.2 Suppose $\|f\|_{H^{-1}(\mathbb {B}^{N})} \leq d_{2}$![]() for $d_{2}>0$
for $d_{2}>0$![]() as given in Proposition 3.4. Then,
as given in Proposition 3.4. Then,
(a) As the $\operatorname {dist}$
 $_{H_{\lambda }(\mathbb {B}^{N})}(v_j,\, \partial \tilde {\Sigma }_+)=\inf \left \{\left \|v_{j}-u\right \|_{H_{\lambda }}: u \in \Sigma,\, u_+ \equiv 0\right \} {\xrightarrow {j}}0$
$_{H_{\lambda }(\mathbb {B}^{N})}(v_j,\, \partial \tilde {\Sigma }_+)=\inf \left \{\left \|v_{j}-u\right \|_{H_{\lambda }}: u \in \Sigma,\, u_+ \equiv 0\right \} {\xrightarrow {j}}0$ implies $J_{\lambda,a, f}(v_{j}) \rightarrow \infty$
implies $J_{\lambda,a, f}(v_{j}) \rightarrow \infty$ .
.(b) Suppose that $\left \{v_{j}\right \}_{j=1}^{\infty } \subset \tilde {\Sigma }_+$
 satisfies as $j \rightarrow \infty$
satisfies as $j \rightarrow \infty$

Then there exists a subsequence—still denoted by $\left \{v_{j}\right \}_{j=1}^{\infty }$![]() , a critical point $u_{0}(x) \in H^{1}(\mathbb {B}^{N})$
, a critical point $u_{0}(x) \in H^{1}(\mathbb {B}^{N})$![]() of $I_{\lambda,a, f}(u)$
of $I_{\lambda,a, f}(u)$![]() , an integer $\ell \in \mathbb {N} \cup \{0\}$
, an integer $\ell \in \mathbb {N} \cup \{0\}$![]() and $\ell$
and $\ell$![]() sequences of points $\left \{y_{j}^{1}\right \}_{j=1}^{\infty },\, \ldots,\,\left \{y_{j}^{\ell }\right \}_{j=1}^{\infty } \subset \mathbb {B}^{N}$
sequences of points $\left \{y_{j}^{1}\right \}_{j=1}^{\infty },\, \ldots,\,\left \{y_{j}^{\ell }\right \}_{j=1}^{\infty } \subset \mathbb {B}^{N}$![]() such that
such that
(1) $d(y_{j}^{k},\,0) \rightarrow \infty \textrm { as } j \rightarrow \infty \;\;\forall k=1,\,2,\, \ldots,\, \ell,$

(2) $d(y_{j}^{k},\,y_{j}^{k^{\prime }}) \rightarrow \infty \textrm { as } j \rightarrow \infty \textrm { for } k \neq k^{\prime },$

(3) $\left \| v_{j}(x)-\frac {u_{0}(x)+\sum _{k=1}^{\ell } w(\tau _{-y_{j}^{k}}(x))}{\left \|u_{0}(x)+\sum _{k=1}^{\ell } w(\tau _{-y_{j}^{k}}(x))\right \|_{{H_{\lambda }}}}\right \|_{{H_{\lambda }}} \rightarrow 0 \textrm { as } j \rightarrow \infty,\,\\ \textrm { where } \tau _a,\, a \in \mathbb {B}^{N} \textrm { denotes the hyperbolic translation,\,}$

(4) $J_{\lambda,a, f}(v_{j}) \rightarrow I_{\lambda,a, f}(u_{0})+\ell I_{\lambda,1,0}(w) \textrm { as } j \rightarrow \infty.$

Proof. For any $\varepsilon \in (0,\,1)$![]() and using (3.12) and (3.6), we obtain,
and using (3.12) and (3.6), we obtain,

As $\operatorname {dist}(v_{j},\, \partial \tilde {\Sigma }_+) \rightarrow 0$![]() gives
gives

Therefore,
Hence $J_{\lambda,a, f}(v_{j}) \rightarrow \infty$![]() as dist $_{H^{1}(\mathbb {B}^{N})}(v_{j},\, \partial \tilde {\Sigma }_+) \rightarrow 0.$
as dist $_{H^{1}(\mathbb {B}^{N})}(v_{j},\, \partial \tilde {\Sigma }_+) \rightarrow 0.$![]() This proves part $(a).$
This proves part $(a).$![]()
For part $(b),$![]() using (3.13) and (3.15), we get
using (3.13) and (3.15), we get

Further, we also have $I_{\lambda,a, f}(t_{a,f}(v_{j})v_{j})=J_{\lambda,a, f}(v_{j}) \rightarrow c$![]() as $j \rightarrow \infty$
as $j \rightarrow \infty$![]() . Applying Palais–Smale lemma for $I_{\lambda,a, f}(u)$
. Applying Palais–Smale lemma for $I_{\lambda,a, f}(u)$![]() (Proposition 4.1), the rest follows.
(Proposition 4.1), the rest follows.
The subsequent corollary is an outcome of the above Proposition 4.2. Before moving to the corollary, note that we say $J_{\lambda,a, f}(v)$![]() satisfies $(\mathrm {PS})_{c}$
satisfies $(\mathrm {PS})_{c}$![]() if and only if any sequence $(v_{j})_{j=1}^{\infty } \subseteq$
if and only if any sequence $(v_{j})_{j=1}^{\infty } \subseteq$![]() $\tilde {\Sigma }_+$
$\tilde {\Sigma }_+$![]() satisfying (4.1) has a strongly convergent subsequence in $H^{1}(\mathbb {B}^{N})$
satisfying (4.1) has a strongly convergent subsequence in $H^{1}(\mathbb {B}^{N})$![]() .
.
Corollary 4.3 Suppose that $\|f\|_{H^{-1}(\mathbb {B}^{N})} \leq d_{2}$![]() for $d_{2}$
for $d_{2}$![]() as in Proposition 3.4. Then $J_{\lambda, a, f}(v)$
as in Proposition 3.4. Then $J_{\lambda, a, f}(v)$![]() satisfies the condition $(\mathrm {PS})_{c}$
satisfies the condition $(\mathrm {PS})_{c}$![]() for $c< I_{\lambda, a, f}(\mathcal {U}_{a, f} (x))+I_{\lambda,1,0}(w)$
for $c< I_{\lambda, a, f}(\mathcal {U}_{a, f} (x))+I_{\lambda,1,0}(w)$![]() where $w$
where $w$![]() is the unique radial solution of (3.1) and $\mathcal {U}_{a, f}$
is the unique radial solution of (3.1) and $\mathcal {U}_{a, f}$![]() is the critical point of $I_{\lambda, a, f}$
is the critical point of $I_{\lambda, a, f}$![]() obtained in Proposition 7.1.
obtained in Proposition 7.1.
Proof. Proposition 4.2 suggests that the condition (PS)$_{c}$![]() breaks down only at levels
breaks down only at levels
where $\ell \in \mathbb {N}$![]() and $u_{0} \in H^{1}(\mathbb {B}^{N})$
and $u_{0} \in H^{1}(\mathbb {B}^{N})$![]() is a critical point of $I_{\lambda,a, f}(u)$
is a critical point of $I_{\lambda,a, f}(u)$![]() .
.
From Proposition 7.1, we have
Furthermore, all the critical points of $I_{\lambda,a, f}(u)$![]() except $\mathcal {U}_{a, f} (x)$
except $\mathcal {U}_{a, f} (x)$![]() corresponds to a critical point $J_{\lambda,a, f}(v)$
corresponds to a critical point $J_{\lambda,a, f}(v)$![]() , which follows from (8.3). Thus there exists $v_{1} \in \tilde {\Sigma }_+$
, which follows from (8.3). Thus there exists $v_{1} \in \tilde {\Sigma }_+$![]() for a critical point $u_{1}$
for a critical point $u_{1}$![]() of $I_{\lambda,a,f}(u)$
of $I_{\lambda,a,f}(u)$![]() such that $I_{\lambda,a, f}(u_{1})=J_{\lambda,a, f}(v_{1})>0$
such that $I_{\lambda,a, f}(u_{1})=J_{\lambda,a, f}(v_{1})>0$![]() by using $(iii)$
by using $(iii)$![]() of Lemma 3.2. Consequently,
of Lemma 3.2. Consequently,
Hence $I_{\lambda,a, f}(\mathcal {U}_{a, f} (x))+I_{\lambda,1,0}(w)$![]() is the lowest level where $(P S)_{c}$
is the lowest level where $(P S)_{c}$![]() breaks.
breaks.
5. Asymptotic estimates for solutions of (𝒫′)
This section is devoted to deriving asymptotic estimates for positive solutions to (𝒫′) for $\lambda \leq 0$![]() . It is worth noting that when $f \equiv 0,$
. It is worth noting that when $f \equiv 0,$![]() the precise estimates were obtained by Sandeep–Mancini in their seminal paper (See [Reference Mancini and Sandeep29, Lemma 3.4]) and has been slightly improved in [Reference Bonforte, Gazzola, Grillo and Vazquez10] for $\lambda =0.$
the precise estimates were obtained by Sandeep–Mancini in their seminal paper (See [Reference Mancini and Sandeep29, Lemma 3.4]) and has been slightly improved in [Reference Bonforte, Gazzola, Grillo and Vazquez10] for $\lambda =0.$![]() Indeed they showed using the moving plane method that all positive solutions to the homogeneous equation are radial with respect to a point. Further, asymptotic was obtained by analysing the corresponding ode. On the other hand, when dealing with $f\not \equiv 0$
Indeed they showed using the moving plane method that all positive solutions to the homogeneous equation are radial with respect to a point. Further, asymptotic was obtained by analysing the corresponding ode. On the other hand, when dealing with $f\not \equiv 0$![]() and non-radial, the solution $u$
and non-radial, the solution $u$![]() need not be radial; hence, this approach does not help us obtain asymptotic estimates for solutions of (𝒫′) Thus we follow the approach of constructing suitable barriers as sub and super-solutions to obtain the desired asymptotic estimates. When $f \equiv 0,$
need not be radial; hence, this approach does not help us obtain asymptotic estimates for solutions of (𝒫′) Thus we follow the approach of constructing suitable barriers as sub and super-solutions to obtain the desired asymptotic estimates. When $f \equiv 0,$![]() we recover the optimal estimates obtained by Sandeep-Mancini [Reference Mancini and Sandeep29] and and also ([Reference Bonforte, Gazzola, Grillo and Vazquez10], $\lambda =0$
we recover the optimal estimates obtained by Sandeep-Mancini [Reference Mancini and Sandeep29] and and also ([Reference Bonforte, Gazzola, Grillo and Vazquez10], $\lambda =0$![]() ) for radial solutions. In particular, we prove the following theorem:
) for radial solutions. In particular, we prove the following theorem:
Theorem 5.1 Let $u$![]() be a positive solution of (𝒫′) and $f \in L^2(\mathbb {B}^{N}),$
be a positive solution of (𝒫′) and $f \in L^2(\mathbb {B}^{N}),$![]() non-negative and assume
non-negative and assume
for all $x \in \mathbb {B}^{N}$![]() and for some positive constants $k,\,C,$
and for some positive constants $k,\,C,$![]() and $\varepsilon.$
and $\varepsilon.$![]()
Then, for any $\delta >0$![]() , there exist positive constants $C_{1},\, C_{2}$
, there exist positive constants $C_{1},\, C_{2}$![]() such that
such that
for all $x \in \mathbb {B}^{N},$![]() and $\lambda = 0.$
and $\lambda = 0.$![]() Furthermore, for $\lambda < 0$
Furthermore, for $\lambda < 0$![]() , there exist positive constants $C^{'}_{1},\, C^{'}_{2}$
, there exist positive constants $C^{'}_{1},\, C^{'}_{2}$![]() such that
such that
for all $x \in \mathbb {B}^{N}$![]() and $c^{'}(n,\,\lambda )=\frac {(N-1)+\sqrt {(N-1)^{2}-4\lambda }}{2|\lambda |}$
and $c^{'}(n,\,\lambda )=\frac {(N-1)+\sqrt {(N-1)^{2}-4\lambda }}{2|\lambda |}$![]() .
.
Proof. The solution $u \in H^1(\mathbb {B}^{N}),$![]() this immediately implies $\lim _{d(x,0) \rightarrow \infty } u(x)=0 \textrm {a.e.}$
this immediately implies $\lim _{d(x,0) \rightarrow \infty } u(x)=0 \textrm {a.e.}$![]() Furthermore, using the Calderon–Zygmund estimate and elliptic regularity, we have $u \in C^{2}(\mathbb {B}^{N})$
Furthermore, using the Calderon–Zygmund estimate and elliptic regularity, we have $u \in C^{2}(\mathbb {B}^{N})$![]() ; thus, $\lim _{d(x,0) \rightarrow \infty } u(x)=0$
; thus, $\lim _{d(x,0) \rightarrow \infty } u(x)=0$![]() for all $x \in \mathbb {B}^{N}.$
for all $x \in \mathbb {B}^{N}.$![]() The proof is divided into two cases: $\lambda < 0$
The proof is divided into two cases: $\lambda < 0$![]() and $\lambda =0.$
and $\lambda =0.$![]()
Case 1: $\lambda < 0$![]()
Choose $\alpha >0$![]() such that $\frac {\alpha ^{2}|\lambda |-1}{\alpha (N-1)}\geq 1$
such that $\frac {\alpha ^{2}|\lambda |-1}{\alpha (N-1)}\geq 1$![]() . To be precise, $\alpha \in [c^{'}(N,\,\lambda ),\, \infty )$
. To be precise, $\alpha \in [c^{'}(N,\,\lambda ),\, \infty )$![]() where
where
Thus we can choose $R_{1}>0$![]() large enough such that
large enough such that
For $m=\min \left \{\frac {1}{|\lambda |}u(x)\mid d(x,\,0) =R_{1}\right \}>0$![]() , set $v_{1}(x) := v_1(r) = m e^{-\alpha |\lambda | (d(x,0)-R_{1})},$
, set $v_{1}(x) := v_1(r) = m e^{-\alpha |\lambda | (d(x,0)-R_{1})},$![]() where $r := d(x,\, 0).$
where $r := d(x,\, 0).$![]() Now for any $L>R_{1}$
Now for any $L>R_{1}$![]() , denote
, denote
Then $\Omega (L)$![]() is open. Moreover, for $x \in \Omega (L)$
is open. Moreover, for $x \in \Omega (L)$![]() and using (5.1) we have
and using (5.1) we have

Applying the maximum principle, for $x \in \Omega (L)$![]() will result in
will result in

Since $\displaystyle \lim _{d(x,0) \rightarrow +\infty } u(x)=\lim _{d(x,0) \rightarrow +\infty } v_{2}(x)=0$![]() , by letting $L \rightarrow \infty$
, by letting $L \rightarrow \infty$![]() , we see that $\Omega (L)$
, we see that $\Omega (L)$![]() is empty and hence
is empty and hence
By the supposition on $f(x)$![]() there exists some $\varepsilon,\, \textrm { and } C>0$
there exists some $\varepsilon,\, \textrm { and } C>0$![]() such that
such that
(5.2) will imply the existence of a $C_{1}>0$![]()
Choosing $\varepsilon$![]() appropriately, and using (5.3), (5.4) together will provide $R_{2}>0$
appropriately, and using (5.3), (5.4) together will provide $R_{2}>0$![]() such that
such that
Moreover, since $p >1,$![]() there holds
there holds
Let $\beta >0$![]() be such that $\beta ^{2}|\lambda |- (N-1)\beta \leq 1$
be such that $\beta ^{2}|\lambda |- (N-1)\beta \leq 1$![]() , i.e., $\beta \leq c(n,\, \lambda )^{'}.$
, i.e., $\beta \leq c(n,\, \lambda )^{'}.$![]()
Define $v_{2}(x)=M e^{-\beta |\lambda |(d(x,0)-R_{4})}$![]() , where
, where
Further, for any $L>R_{4}$![]() , denote
, denote
Then $\tilde {\Omega }(L)$![]() is open and, for $x \in \tilde {\Omega }(L)$
is open and, for $x \in \tilde {\Omega }(L)$![]() ,
,

By the maximum principle, for $x \in \widetilde {\Omega }(L)$![]() ,
,

Since $\displaystyle \lim _{d(x,0) \rightarrow +\infty } u(x)=\lim _{d(x,0) \rightarrow +\infty } v_{2}(x)=0$![]() , by letting $L \rightarrow \infty$
, by letting $L \rightarrow \infty$![]() , we see again that $\tilde {\Omega }(L)$
, we see again that $\tilde {\Omega }(L)$![]() is empty and hence
is empty and hence
Now by choosing $\alpha = \beta = c^{'}(N,\,\lambda ),$![]() the proof is complete.
the proof is complete.
Case 2: $\lambda =0$![]()
This case can also be tackled similarly by appropriately choosing the functions $v_{1}$![]() and $v_{2}$
and $v_{2}$![]() .
.
To be precise, let
where $m=\min \left \{u(x)\mid d(x,\,0) =R_{1}^{'}\right \}>0$![]() and $M=\max \left \{u(x)\mid d(x,\,0) =R_{2}^{'}\right \} >0.$
and $M=\max \left \{u(x)\mid d(x,\,0) =R_{2}^{'}\right \} >0.$![]()
Indeed $\gamma >0$![]() satisfies $\gamma > N-1$
satisfies $\gamma > N-1$![]() , and thus $R_{1}^{'}$
, and thus $R_{1}^{'}$![]() is chosen such that $\gamma - (N-1) \coth {r} > 0$
is chosen such that $\gamma - (N-1) \coth {r} > 0$![]() for all $r > R_{1}^{'}.$
for all $r > R_{1}^{'}.$![]() Also, $R_{2}^{'}$
Also, $R_{2}^{'}$![]() is chosen similarly as $R_{3}$
is chosen similarly as $R_{3}$![]() mentioned above. Further, we can conclude the lemma by applying the maximum principle in the hyperbolic balls of radius $R_{1}^{'}$
mentioned above. Further, we can conclude the lemma by applying the maximum principle in the hyperbolic balls of radius $R_{1}^{'}$![]() and $R_{2}^{'}$
and $R_{2}^{'}$![]() and proceeding as in the previous case.
and proceeding as in the previous case.
6. Key Energy Estimates
This section is devoted to deriving key energy estimates for the functional $I_{\lambda, a, f}$![]() with $a(x) \leq 1$
with $a(x) \leq 1$![]() . The subsequent energy estimates will play a pivotal role in the existence of solutions. In fact with the help of the proposition 6.1, we shall show that the energy of the functional is below the critical level given in the Palais–Smale decomposition.
. The subsequent energy estimates will play a pivotal role in the existence of solutions. In fact with the help of the proposition 6.1, we shall show that the energy of the functional is below the critical level given in the Palais–Smale decomposition.
Proposition 6.1 Let $a$![]() satisfies $0< a \in L^{\infty }(\mathbb {B}^{N}),\, a(x) \rightarrow 1$
satisfies $0< a \in L^{\infty }(\mathbb {B}^{N}),\, a(x) \rightarrow 1$![]() as $d(x,\,0) \rightarrow \infty$
as $d(x,\,0) \rightarrow \infty$![]() and (1.4). Further, assume that $\|f\|_{H^{-1}(\mathbb {B}^{N})}{\leq }\; d_{2},\,\; f \geq 0,\,\; f \not \equiv 0$
and (1.4). Further, assume that $\|f\|_{H^{-1}(\mathbb {B}^{N})}{\leq }\; d_{2},\,\; f \geq 0,\,\; f \not \equiv 0$![]() and $\tilde {\mathcal {U}}_{a, f}$
and $\tilde {\mathcal {U}}_{a, f}$![]() is any critical point of $I_{\lambda,a,f}$
is any critical point of $I_{\lambda,a,f}$![]() . Then there exists $R > 0$
. Then there exists $R > 0$![]() such that
such that
for all $d(y,\,0) \geq R$![]() and $t>0$
and $t>0$![]() .
.
Moreover, if $a$![]() satisfies $(\mathbf {A}_{3}),$
satisfies $(\mathbf {A}_{3}),$![]() i.e., $a \equiv 1$
i.e., $a \equiv 1$![]() , we have
, we have
for all $d(y,\,0) \geq R.$![]()
Proof. Performing straightforward calculations implies

Now for all $h \in H^{1}(\mathbb {B}^{N})$![]() , we have
, we have

i.e.,
In particular, for $h=t w(\tau _{-y}(x))$![]() in the above yields
in the above yields

Hence utilizing the above equation and appropriately rearranging the terms in (6.3) will result in

where
and

To complete the proof of the proposition, we need to show that $(I) \; -\;(II) < 0,$![]() for suitably chosen $R >0.$
for suitably chosen $R >0.$![]()
Using the continuity, we easily get
as $t \rightarrow 0$![]() . In addition, we also have
. In addition, we also have
Thus using the above two facts, we can find $m,\, M$![]() with $0< m< M$
with $0< m< M$![]() such that
such that

As a result, to prove the proposition at hand, it suffices to show (6.1) for $t \in [m,\, M]$![]() . Hence to finish the proof, we need to show $I< II$
. Hence to finish the proof, we need to show $I< II$![]() . To this end, let us recall the following standard $p$
. To this end, let us recall the following standard $p$![]() th inequalities from calculus.
th inequalities from calculus.
(1) $(s+t)^{p+1}-s^{p+1}-t^{p+1}-(p+1) s^{p} t \geq 0$
 for all $(s,\, t) \in [0,\, \infty ) \times [0,\, \infty )$
for all $(s,\, t) \in [0,\, \infty ) \times [0,\, \infty )$ .
.(2) For any $r > 0$
 we can find a constant $A(r) > 0$
we can find a constant $A(r) > 0$ such that
\[ (s+t)^{p+1}-s^{p+1}-t^{p+1}-(p+1) s^{p} t \geq A(r) t^{2}, \]for all $(s,\, t) \in [r,\, \infty ) \times [0,\, \infty )$
such that
\[ (s+t)^{p+1}-s^{p+1}-t^{p+1}-(p+1) s^{p} t \geq A(r) t^{2}, \]for all $(s,\, t) \in [r,\, \infty ) \times [0,\, \infty )$
 .
.
We can estimate $II$![]() with the help of the above inequality as follows:
with the help of the above inequality as follows:
Set $A:=A(r):=A(\min _{d(x,0) \leq 1} \tilde {\mathcal {U}}_{a, f}(x))>$![]() 0, then
0, then

Estimate of $E_1:$![]() We shall estimate $E_1$
We shall estimate $E_1$![]() in the domain $d(x,\, 0) \leq 1.$
in the domain $d(x,\, 0) \leq 1.$![]() Using traingle inequality we have
Using traingle inequality we have
Since, $d(x,\, 0) \leq 1,$![]() there exist $R > 0$
there exist $R > 0$![]() and $\varepsilon _{R} > 0$
and $\varepsilon _{R} > 0$![]() such that whenver $d(y,\, 0) > R,$
such that whenver $d(y,\, 0) > R,$![]() there holds
there holds
where $\varepsilon _R \rightarrow 0$![]() as $R \rightarrow \infty.$
as $R \rightarrow \infty.$![]() Thus using above and (3.2) we conclude for any $\varepsilon > 0,$
Thus using above and (3.2) we conclude for any $\varepsilon > 0,$![]()

Therefore we have
Estimate of I : Let us now compute an estimate on $I$![]() for $\delta > c(n,\, \lambda )(p+1)+(N-1)$
for $\delta > c(n,\, \lambda )(p+1)+(N-1)$![]() , then for every $\varepsilon ^{\prime } >0,\,\\ \delta >(c(n,\, \lambda )- \varepsilon ^{\prime })(p+1)+(N-1).$
, then for every $\varepsilon ^{\prime } >0,\,\\ \delta >(c(n,\, \lambda )- \varepsilon ^{\prime })(p+1)+(N-1).$![]() We shall estimate $I$
We shall estimate $I$![]() as follows:
as follows:

Thus we have deduced
Now applying(6.6) and (6.8), we can choose $R_{0}>R>0$![]() large enough and also choose ${\varepsilon }$
large enough and also choose ${\varepsilon }$![]() and $\varepsilon ^{\prime }$
and $\varepsilon ^{\prime }$![]() appropriately such that
appropriately such that
As a result, (6.1) is proved. This completes the proof (6.1). Now the proof of (6.2) can be concluded in a similar line by noting that $(I)$![]() is zero and $\underline {a} =1.$
is zero and $\underline {a} =1.$![]()
7. Proof of Theorem 1.1 and Theorem 1.4
7.1. Existence of the first solution of ($\mathcal {P}$ ) for $a(x)$
) for $a(x)$ satisfying $(\mathbf {A}_{1})$
satisfying $(\mathbf {A}_{1})$ or $(\mathbf {A}_{3})$
or $(\mathbf {A}_{3})$
The below-mentioned proposition helps us establish the existence of the first positive solution in the neighbourhood of 0.
Proposition 7.1 For $d_{0}$![]() as chosen in Lemma 3.2 and $a(x)$
as chosen in Lemma 3.2 and $a(x)$![]() satisfying $(\mathbf {A}_{1})$
satisfying $(\mathbf {A}_{1})$![]() or $(\mathbf {A}_{3})$
or $(\mathbf {A}_{3})$![]() , there exists $r_{1}>0$
, there exists $r_{1}>0$![]() and $d_{1}\in (0,\, d_0]$
and $d_{1}\in (0,\, d_0]$![]() such that
such that
(i) $I_{\lambda,a, f}(u)$
 is strictly convex in $B(r_{1})=\left \{u \in H^{1}(\mathbb {B}^{N})\right.$
is strictly convex in $B(r_{1})=\left \{u \in H^{1}(\mathbb {B}^{N})\right.$ : $\left.\|u\|_{H_{\lambda }}< r_{1}\right \}$
: $\left.\|u\|_{H_{\lambda }}< r_{1}\right \}$ .
.(ii) If $\|f\|_{H^{-1}(\mathbb {B}^{N})} \leq d_{1}$
 , then
\[ \inf _{\|u\|_{H_{\lambda}}=r_{1}} I_{\lambda,a, f}(u)>0 . \]
, then
\[ \inf _{\|u\|_{H_{\lambda}}=r_{1}} I_{\lambda,a, f}(u)>0 . \]
Moreover, there exists a unique critical point $\mathcal {U}_{a, f}(x)$![]() of $I_{\lambda,a, f}(u)$
of $I_{\lambda,a, f}(u)$![]() in $B(r_{1})$
in $B(r_{1})$![]() . Furthermore, $\mathcal {U}_{a, f}(x)$
. Furthermore, $\mathcal {U}_{a, f}(x)$![]() satisfies
satisfies
Proof. We proceed to prove part $(i)$![]() as follows:
as follows:
Applying Hölder inequality, Sobolev inequality and the fact that $a \leq 1$![]() or $a \equiv 1$
or $a \equiv 1$![]() , we get an estimate on the second term of RHS of (7.1) as follows
, we get an estimate on the second term of RHS of (7.1) as follows

Thus using this above estimate in (7.1) yields
Defining $r_{1}=p^{-\frac {1}{p-1}} S_{1,\lambda }^{\frac {p+1}{2(p-1)}}$![]() results in $I_{\lambda,a, f}^{\prime \prime }(u)$
results in $I_{\lambda,a, f}^{\prime \prime }(u)$![]() being positive definite for $u \in B(r_{1})$
being positive definite for $u \in B(r_{1})$![]() . Therefore, $I_{\lambda,a, f}(u)$
. Therefore, $I_{\lambda,a, f}(u)$![]() is strictly convex in $B(r_{1})$
is strictly convex in $B(r_{1})$![]() . We are done with the proof of part $(i)$
. We are done with the proof of part $(i)$![]() .
.
$(ii)$![]() Assuming $\|u\|_{H_{\lambda }}=r_{1}$
Assuming $\|u\|_{H_{\lambda }}=r_{1}$![]() gives
gives

Further,
where we have used $r_{1}^{p-1}=\frac {1}{p} S_{1,\lambda }^{\frac {p+1}{2}}$![]() .
.
Thus there exists $d_{1} \in (0,\, d_{0}]$![]() such that
such that
Moreover, there exists a unique critical point $\mathcal {U}_{a, f}(x)$![]() of $I_{\lambda,a, f}(u)$
of $I_{\lambda,a, f}(u)$![]() in $B(r_{1})$
in $B(r_{1})$![]() because $I_{\lambda,a, f}(u)$
because $I_{\lambda,a, f}(u)$![]() is strictly convex in $B(r_{1})$
is strictly convex in $B(r_{1})$![]() and $\inf _{\|u\|_{H_{\lambda }}=\, r_{1}} I_{\lambda,a, f}(u)>0=I_{\lambda,a, f}(0)$
and $\inf _{\|u\|_{H_{\lambda }}=\, r_{1}} I_{\lambda,a, f}(u)>0=I_{\lambda,a, f}(0)$![]() . Furthermore, this critical point satisfies
. Furthermore, this critical point satisfies
This completes the proof of the proposition.
7.2. The case $a(x) \leq 1,$ $\mu \{ x : a(x) \neq 1 \} >0:$
$\mu \{ x : a(x) \neq 1 \} >0:$ Existence of second and third solutions.
Existence of second and third solutions.
We now aim to prove the existence of the second and third positive solutions. To fulfil this aim, we will utilize the Lusternik–Schnirelman category theory, a careful investigation of Palais–Smale characterization, and energy estimates involving hyperbolic bubbles to prove the multiplicity result. The following notation will be used to define level sets in the subsequent sections.
for $c \in \mathbb {R}$![]() . To compute the critical points of $J_{\lambda,a, f}(v)$
. To compute the critical points of $J_{\lambda,a, f}(v)$![]() , we will show for a sufficiently small $\varepsilon >0$
, we will show for a sufficiently small $\varepsilon >0$![]() ,
,
where cat denotes Lusternik–Schnirelman Category.
We now study the properties of the functional $J_{\lambda,a, 0}$![]() under the condition $\mathbf {A}_{1}$
under the condition $\mathbf {A}_{1}$![]() .
.
Lemma 7.2 Assume $a$![]() satisfies $0< a \in L^{\infty }(\mathbb {B}^{N}),\, a(x) \rightarrow 1$
satisfies $0< a \in L^{\infty }(\mathbb {B}^{N}),\, a(x) \rightarrow 1$![]() as $d(x,\,0) \rightarrow \infty$
as $d(x,\,0) \rightarrow \infty$![]() , (1.4) and $\mathbf {A}_{1}$
, (1.4) and $\mathbf {A}_{1}$![]() . Then there holds
. Then there holds
(i) $\inf _{v \in \tilde {\Sigma }_+} J_{\lambda,a, 0}(v)=I_{\lambda,1,0}(w)$
 .
.(ii) $\inf _{v \in \tilde {\Sigma }_+} J_{\lambda,a, 0}(v)$
 is not attained.
is not attained.(iii) $J_{\lambda,a, 0}(v)$
 satisfies $(P S)_{c}$
satisfies $(P S)_{c}$ for $c \in (-\infty,\, I_{\lambda,1,0}(w)) \cup (I_{\lambda,1,0}(w),\, 2 I_{\lambda,1,0}(w))$
for $c \in (-\infty,\, I_{\lambda,1,0}(w)) \cup (I_{\lambda,1,0}(w),\, 2 I_{\lambda,1,0}(w))$ .
.
Proof. Using (3.8) and $\mathbf {A}_{\mathbf {1}}$![]() , we immediately get
, we immediately get
Now define $w_{l}(x)=w(\tau _{le}(x))$![]() for a unit vector $e$
for a unit vector $e$![]() in $\mathbb {R}^{N}$
in $\mathbb {R}^{N}$![]() and $0< l<1$
and $0< l<1$![]() so that $le \in \mathbb {B}^{N}$
so that $le \in \mathbb {B}^{N}$![]() . Moreover, $l \rightarrow \infty$
. Moreover, $l \rightarrow \infty$![]() in the disc model of the hyperbolic space means $l \rightarrow 1$
in the disc model of the hyperbolic space means $l \rightarrow 1$![]() . Applying Lemma 3.3, corresponding to $\bar {w}_{l}=\frac {w_{l}}{\left \|w_{l}\right \|} \in \tilde {\Sigma }_+$
. Applying Lemma 3.3, corresponding to $\bar {w}_{l}=\frac {w_{l}}{\left \|w_{l}\right \|} \in \tilde {\Sigma }_+$![]() implies the existence of a unique $t_{a, 0}(\bar {w}_{l})$
implies the existence of a unique $t_{a, 0}(\bar {w}_{l})$![]() such that
such that
Let us now determine the RHS of the above equation

Also, $t_{a, 0}(\bar {w}_{l})$![]() can be expressed in an explicit form that occurs in the proof of Lemma 3.3 which is given by
can be expressed in an explicit form that occurs in the proof of Lemma 3.3 which is given by

Since $w$![]() is the unique radial solution of (3.1), we further get
is the unique radial solution of (3.1), we further get

Hence $(i)$![]() follows.
follows.
We will now show $(ii)$![]() by contradiction, i.e., let us assume that there exists $v_{0} \in \tilde {\Sigma }_+$
by contradiction, i.e., let us assume that there exists $v_{0} \in \tilde {\Sigma }_+$![]() such that $J_{\lambda,a, 0}(v_{0})=\inf _{v \in \tilde {\Sigma }_+} J_{\lambda,a, 0}(v)=I_{\lambda,1,0}(w)$
such that $J_{\lambda,a, 0}(v_{0})=\inf _{v \in \tilde {\Sigma }_+} J_{\lambda,a, 0}(v)=I_{\lambda,1,0}(w)$![]() . Define, the Nehari manifold $\mathcal {N}$
. Define, the Nehari manifold $\mathcal {N}$![]() as
as
It is not difficult to find a $t_{v_{0}}>0$![]() such that $t_{v_{0}} v_{0} \in \mathcal {N}$
such that $t_{v_{0}} v_{0} \in \mathcal {N}$![]() . Further, note that that for any $v \in \mathcal {N}$
. Further, note that that for any $v \in \mathcal {N}$![]() , we have $\|v\|_{H_{\lambda }}^{2}=\int _{\mathbb {B}^{N}}(v)_+^{p+1} \mathrm {~d} V_{\mathbb {B}^{N}}$
, we have $\|v\|_{H_{\lambda }}^{2}=\int _{\mathbb {B}^{N}}(v)_+^{p+1} \mathrm {~d} V_{\mathbb {B}^{N}}$![]() , and consequently,
, and consequently,
where $S_{1,\lambda }$![]() is as defined in (3.10). Thus $I_{\lambda,1,0}(v) \geq I_{\lambda,1,0}(w)$
is as defined in (3.10). Thus $I_{\lambda,1,0}(v) \geq I_{\lambda,1,0}(w)$![]() for all $v \in \mathcal {N}$
for all $v \in \mathcal {N}$![]() . Moreover, $w \in \mathcal {N}$
. Moreover, $w \in \mathcal {N}$![]() , and hence
, and hence
Therefore,

Thus the above inequality and $\mathbf {A}_{\mathbf {1}}$![]() result in
result in
Thus
Moreover, the inequality in (7.2) becomes an equality by substituting (7.3) into (7.2). Therefore,
Thus $t_{v_{0}} v_{0}$![]() is a constraint critical point of $I_{\lambda,1,0}$
is a constraint critical point of $I_{\lambda,1,0}$![]() . Therefore $t_{v_{0}} v_{0}>0$
. Therefore $t_{v_{0}} v_{0}>0$![]() follows from the Lagrange multiplier and maximum principle, which further implies $v_{0}>0$
follows from the Lagrange multiplier and maximum principle, which further implies $v_{0}>0$![]() in $\mathbb {B}^{N}$
in $\mathbb {B}^{N}$![]() . This contradicts (7.4). Hence $(2)$
. This contradicts (7.4). Hence $(2)$![]() holds.
holds.
The proof of part $(3)$![]() follows from the Palais–Smale decomposition.
follows from the Palais–Smale decomposition.
Lemma 7.3 Let $a$![]() as in Theorem 1.1. Then there exists a constant $\delta _{0}>0$
as in Theorem 1.1. Then there exists a constant $\delta _{0}>0$![]() such that if $J_{\lambda,a, 0}(v) \leq I_{\lambda,1,0}(w)+\delta _{0}$
such that if $J_{\lambda,a, 0}(v) \leq I_{\lambda,1,0}(w)+\delta _{0}$![]() , then
, then
where $m(x) >0$![]() is defined such that $d(\frac {x}{m},\,0)= \frac {1}{2}$
is defined such that $d(\frac {x}{m},\,0)= \frac {1}{2}$![]() , i.e., $m(x)= \frac {|x|}{\tanh (\frac {1}{4})}.$
, i.e., $m(x)= \frac {|x|}{\tanh (\frac {1}{4})}.$![]()
Proof. Suppose on the contrary that there exists a sequence $\left \{v_{n}\right \} \subset \tilde {\Sigma }_+$![]() such that
such that
Then there exists $\tilde {v}_{n} \subset \tilde {\Sigma }_+$![]() by Ekeland's variational principle such that
by Ekeland's variational principle such that

The above implies $\left \{\tilde {v}_{n}\right \}$![]() is a Palais Smale sequence for $J_{\lambda,a, 0}$
is a Palais Smale sequence for $J_{\lambda,a, 0}$![]() at the level $I_{\lambda,1,0}(w)$
at the level $I_{\lambda,1,0}(w)$![]() .
.
Further, by Proposition 4.2, we have $\left \{y_{n}\right \} \subset \mathbb {B}^{N}$![]() such that $d(y_{n},\,0) \stackrel {n}{\rightarrow } \infty$
such that $d(y_{n},\,0) \stackrel {n}{\rightarrow } \infty$![]() and
and

Therefore,

Thus we can deduce

Hence we have come to a contradiction.
Finally, in this section, we state some refinement of Corollary 4.3.
Proposition 7.4 Assume $a$![]() as in Lemma 1.1. Then for any $\varepsilon >0$
as in Lemma 1.1. Then for any $\varepsilon >0$![]() , there exists $d(\varepsilon ) \in (0,\, d_{2}]$
, there exists $d(\varepsilon ) \in (0,\, d_{2}]$![]() such that for $\|f\|_{H^{-1}(\mathbb {B}^{N})} \leq d(\varepsilon )$
such that for $\|f\|_{H^{-1}(\mathbb {B}^{N})} \leq d(\varepsilon )$![]() , the following holds
, the following holds
(i) $\inf _{v \in \tilde {\Sigma }_+} J_{\lambda,a, f}(v) \in [I_{\lambda,1,0}(\omega )-\varepsilon,\, I_{\lambda,1,0}(\omega )+\varepsilon ]$
 .
.(ii) $J_{\lambda,a, f}(v)$
 satisfies $(\mathrm {PS})_{c}$
satisfies $(\mathrm {PS})_{c}$ for
\begin{align*} c \in & \left(-\infty, I_{\lambda,a, f}\left(u_{l o c \min }(a, f ; x)\right)+I_{\lambda,1,0}(\omega)\right) \\ & \cup\left(I_{\lambda,a, f}\left(u_{\text{loc } \min }(a, f ; x)\right)+I_{\lambda,1,0}(\omega), 2 I_{\lambda,1,0}(\omega)-\varepsilon\right) . \end{align*}
for
\begin{align*} c \in & \left(-\infty, I_{\lambda,a, f}\left(u_{l o c \min }(a, f ; x)\right)+I_{\lambda,1,0}(\omega)\right) \\ & \cup\left(I_{\lambda,a, f}\left(u_{\text{loc } \min }(a, f ; x)\right)+I_{\lambda,1,0}(\omega), 2 I_{\lambda,1,0}(\omega)-\varepsilon\right) . \end{align*}
Now Lusternik–Schnirelmn (L–S) category theory will help us find the second and third positive solutions to ($\mathcal {P}$![]() ). Note that the $(L-S)$
). Note that the $(L-S)$![]() category of $A$
category of $A$![]() with respect to $M$
with respect to $M$![]() is denoted by cat $(A,\, M)$
is denoted by cat $(A,\, M)$![]() . Particularly, cat $(M)$
. Particularly, cat $(M)$![]() denotes cat $(M,\, M)$
denotes cat $(M,\, M)$![]() .
.
The following proposition is vital to obtain the second and third solutions to ($\mathcal {P}$![]() ).
).
Proposition 7.5 Suppose $M$![]() is a Hilbert manifold and $\Psi \in C^{1}(M,\, \mathbb {R})$
is a Hilbert manifold and $\Psi \in C^{1}(M,\, \mathbb {R})$![]() . Assume that for $c_{0} \in \mathbb {R}$
. Assume that for $c_{0} \in \mathbb {R}$![]() and $k \in \mathbb {N}$
and $k \in \mathbb {N}$![]()
(i) $\Psi (x)$
 satisfies $(P S)_{c}$
satisfies $(P S)_{c}$ for $c \leq c_{0}.$
for $c \leq c_{0}.$
(ii) $\operatorname {cat}(\left \{x \in M: \Psi (x) \leq c_{0}\right \}) \geq k.$

Then $\Psi (x)$![]() has at least $k$
has at least $k$![]() critical points in $\left \{x \in M: \Psi (x) \leq c_{0}\right \}$
critical points in $\left \{x \in M: \Psi (x) \leq c_{0}\right \}$![]() .
.
Lemma 7.6 [Reference Adachi and Tanaka2], lemma 2.5
Let $N \geq 1$![]() and $M$
and $M$![]() be a topological space. Assume that there exist two continuous mappings
be a topological space. Assume that there exist two continuous mappings
such that $G \circ F$![]() is homotopic to the identity map Id: $S^{N-1}_{\mathbb {B}^{N}} \rightarrow S^{N-1}_{\mathbb {B}^{N}}$
is homotopic to the identity map Id: $S^{N-1}_{\mathbb {B}^{N}} \rightarrow S^{N-1}_{\mathbb {B}^{N}}$![]() , i.e, there is a continuous $\operatorname {map} \eta :[0,\,1] \times S^{N-1}_{\mathbb {B}^{N}} \rightarrow S^{N-1}_{\mathbb {B}^{N}}$
, i.e, there is a continuous $\operatorname {map} \eta :[0,\,1] \times S^{N-1}_{\mathbb {B}^{N}} \rightarrow S^{N-1}_{\mathbb {B}^{N}}$![]() such that
such that

Then cat $(M) \geq 2$![]() .
.
Taking into account the above lemma, our next goal will be to construct two mappings:

such that $G \circ F$![]() is homotopic to the identity map.
is homotopic to the identity map.
Let us define $F_{R}: S^{N-1}_{\mathbb {B}^{N}} \rightarrow \tilde {\Sigma }_+$![]() as follows:
as follows:
For $d(y,\,0) \geq R_{0}$![]() , where $R_{0}$
, where $R_{0}$![]() is as found in Proposition 6.1, (6.1) holds for all $t > 0$
is as found in Proposition 6.1, (6.1) holds for all $t > 0$![]() . For $d(y,\,0) \geq R_{0}$
. For $d(y,\,0) \geq R_{0}$![]() , we will find $s=s(f,\, y)$
, we will find $s=s(f,\, y)$![]() such that
such that

This implies

Therefore,

Proposition 7.7 [Reference Adachi and Tanaka2], proposition 2.6
Assume $a$![]() as in Theorem 1.1. Then there exists $d_{3} \in (0,\, d_{2}]$
as in Theorem 1.1. Then there exists $d_{3} \in (0,\, d_{2}]$![]() and $R_{1}>R_{0}$
and $R_{1}>R_{0}$![]() such that for any $\|f\|_{H^{-1}(\mathbb {B}^{N})} \leq d_{3}$
such that for any $\|f\|_{H^{-1}(\mathbb {B}^{N})} \leq d_{3}$![]() and any $d(y,\,0) \geq R_{1}$
and any $d(y,\,0) \geq R_{1}$![]() , there exists a unique $s=s(f,\, y)>0$
, there exists a unique $s=s(f,\, y)>0$![]() in a neighbourhood of 1, satisfying (7.6). In addition,
in a neighbourhood of 1, satisfying (7.6). In addition,
is continuous.
Now we define a function $F_{R}: S^{N-1}_{\mathbb {B}^{N}} \rightarrow \tilde {\Sigma }_+$![]() by
by

for $\|f\|_{H^{-1}(\mathbb {B}^{N})} \leq d_{3}$![]() and $R \geq R_{1}$
and $R \geq R_{1}$![]() .
.
Then we have,
Proposition 7.8 For $0<\|f\|_{H^{-1}(\mathbb {B}^{N})} \leq d_{3}$![]() and $R \geq R_{1}$
and $R \geq R_{1}$![]() , there exists $\varepsilon _{0} = \varepsilon _{0}(R)>0$
, there exists $\varepsilon _{0} = \varepsilon _{0}(R)>0$![]() such that
such that
Proof. The following expression follows from the construction of $F_{R}$![]()
Hence the proposition follows as $F(S^{N-1}_{\mathbb {B}^{N}})$![]() is compact.
is compact.
Thus we construct a mapping
Now the following lemma is crucial for constructing the mapping $G$![]() .
.
Lemma 7.9 There exists $d_{4} \in (0,\, d_{3}]$![]() such that if $\|f\|_{H^{-1}(\mathbb {B}^{N})} \leq d_{4}$
such that if $\|f\|_{H^{-1}(\mathbb {B}^{N})} \leq d_{4}$![]() , then
, then
where $\delta _{0}>0$![]() is as found in lemma 7.3.
is as found in lemma 7.3.
Proof. for any $\varepsilon \in (0,\,1)$![]() , the following holds using (3.12)
, the following holds using (3.12)
Now, if
then
because $I_{\lambda,a, f}(\mathcal {U}_{a, f} (x)) \leq 0$![]() .
.
Therefore, (7.8) implies
for all $v \in [J_{\lambda,a, f} \leq I_{\lambda,a, f}(\mathcal {U}_{a, f} (x))+I_{\lambda,1,0}(w)].$![]()
Thus $v \in [J_{\lambda,a, 0} \leq (1-\varepsilon )^{-\frac {p+1}{p-1}}(I_{\lambda,1,0}(w)+\frac {1}{2 \varepsilon }\|f\|_{H^{-1}(\mathbb {B}^{N})}^{2})]$![]() .
.
Since $\varepsilon \in (0,\,1)$![]() is arbitrary, we get
is arbitrary, we get
Hence (7.7) follows.
We are now in a position to define the function $G$![]() as follows:
as follows:

where $m$![]() as defined in Lemma 7.3, and the above function is well defined again by Lemma 7.3 and by Lemma 7.9. Besides, we will show that these developments, i.e., $F$
as defined in Lemma 7.3, and the above function is well defined again by Lemma 7.3 and by Lemma 7.9. Besides, we will show that these developments, i.e., $F$![]() and $G$
and $G$![]() will serve our purpose.
will serve our purpose.
Proposition 7.10 For a sufficiently large $R \geq R_{1}$![]() and for sufficiently small $\|f\|_{H^{-1}(\mathbb {B}^{N})}>0$
and for sufficiently small $\|f\|_{H^{-1}(\mathbb {B}^{N})}>0$![]() , we have,
, we have,
is homotopic to identity.
Proof. The proof follows as in [Reference Adachi and Tanaka2].
We are now in a situation to establish our main results:
Proposition 7.11 For sufficiently large $R \geq R_{1}$![]() ,
,
The above proposition led us to the following multiplicity results.
Theorem 7.12 Let $a$![]() satisfy the assumptions as in Theorem 1.1. Then there exists $d_{5}>0$
satisfy the assumptions as in Theorem 1.1. Then there exists $d_{5}>0$![]() such that if $\|f\|_{H^{-1}(\mathbb {B}^{N})} \leq d_{5},\,\; f \geq 0,\,\; f \not \equiv 0$
such that if $\|f\|_{H^{-1}(\mathbb {B}^{N})} \leq d_{5},\,\; f \geq 0,\,\; f \not \equiv 0$![]() , then $J_{\lambda,a, f}(v)$
, then $J_{\lambda,a, f}(v)$![]() has at least two critical points in
has at least two critical points in
We can now finish the proof of Theorem 1.1 as follows:
Firstly, set $u^{(1)}(x)=\mathcal {U}_{a, f} (x)$![]() as found in Proposition 7.1. Also, using (4.2) $u^{(1)}(x)$
as found in Proposition 7.1. Also, using (4.2) $u^{(1)}(x)$![]() satisfies
satisfies
By Theorem 7.12, $J_{\lambda,a, f}(v)$![]() has at least two critical points $v^{(2)}(x),\, v^{(3)}(x)$
has at least two critical points $v^{(2)}(x),\, v^{(3)}(x)$![]() in
in
Then $u^{(2)}(x)=t_{a, f}(v^{(2)}) v^{(2)}(x),\, u^{(3)}(x)=t_{a, f}(v^{(3)}) v^{(3)}(x)$![]() will be the corresponding solutions to ($\mathcal {P}$
will be the corresponding solutions to ($\mathcal {P}$![]() ) using Proposition 3.4. Moreover, by Lemma 3.2, we get
) using Proposition 3.4. Moreover, by Lemma 3.2, we get

Hence $u^{(1)}(x),\, u^{(2)}(x),\, u^{(3)}(x)$![]() are distinct, and $\mathcal {P}$
are distinct, and $\mathcal {P}$![]() possesses at least three positive solutions.
possesses at least three positive solutions.
7.3. The case $a(x) \equiv 1 :$ Existence of the second solution
Existence of the second solution
The Remark 3.1 suggests that we need to find the critical points of the energy functional $I_{\lambda,1,f}$![]() to guarantee the existence of solutions to (𝒫′).
to guarantee the existence of solutions to (𝒫′).
Proof. There exists $r_{1}>0$![]() such that
such that
where $r_{1}$![]() is as found in Proposition 7.1. Also, using Proposition 7.1 and (4.2), we found a positive solution $\mathcal {U}_{1, f} (x)$
is as found in Proposition 7.1. Also, using Proposition 7.1 and (4.2), we found a positive solution $\mathcal {U}_{1, f} (x)$![]() of (𝒫′) in $B(r_{1})$
of (𝒫′) in $B(r_{1})$![]() with $I_{\lambda,1,f}(\mathcal {U}_{1, f} (x))\leqslant 0$
with $I_{\lambda,1,f}(\mathcal {U}_{1, f} (x))\leqslant 0$![]() .
.
Now fix $y$![]() such that (6.2) holds. Further, it is not difficult to find $t_{0}>0$
such that (6.2) holds. Further, it is not difficult to find $t_{0}>0$![]() such that $I_{\lambda,1,f}(\mathcal {U}_{1, f} (x)+t w(\tau _{y}(x)))<0$
such that $I_{\lambda,1,f}(\mathcal {U}_{1, f} (x)+t w(\tau _{y}(x)))<0$![]() and $\|\mathcal {U}_{1, f} (x)+t w(\tau _{y}(x))\|_{H_{\lambda }} > r_{1}$
and $\|\mathcal {U}_{1, f} (x)+t w(\tau _{y}(x))\|_{H_{\lambda }} > r_{1}$![]() for $t \geqslant t_{0}$
for $t \geqslant t_{0}$![]() .
.
Set

Moreover, we have
which follows from (7.9) and 6.2.
Thus applying the mountain-pass theorem of Ambrosetti and Rabinowitz and then using PS characterisation (4), we get a solution of (𝒫′), say $\mathcal {V}_{1, f}$![]() , such that
, such that
for some non-negative integer $m$![]() . Furthermore, 7.11 and 7.10 imply $\mathcal {U}_{1, f} \neq \mathcal {V}_{1, f}$
. Furthermore, 7.11 and 7.10 imply $\mathcal {U}_{1, f} \neq \mathcal {V}_{1, f}$![]() .
.
We have finished the proof of Theorem 1.4.
8. Proof of Theorem 1.3
In this section, we prove Theorem 1.3 by finding two positive critical points of the functional $I_{\lambda,a, f}$![]() (as defined in (3.3)). We essentially follow the approach in the spirit of Jeanjean [Reference Jeanjean22]. Towards that, we partition $H^{1}(\mathbb {B}^{N})$
(as defined in (3.3)). We essentially follow the approach in the spirit of Jeanjean [Reference Jeanjean22]. Towards that, we partition $H^{1}(\mathbb {B}^{N})$![]() into the following three disjoint sets:
into the following three disjoint sets:

where $g: H^{1}(\mathbb {B}^{N}) \rightarrow \mathbb {R}$![]() is defined as
is defined as
Remark 8.1 Observe that $\|u\|_{H_{\lambda }}$![]() and $\|u\|_{L^{p+1}(\mathbb {B}^{N})}$
and $\|u\|_{L^{p+1}(\mathbb {B}^{N})}$![]() are bounded away from 0 for all $u \in U$
are bounded away from 0 for all $u \in U$![]() . It follows from the fact that $p>1$
. It follows from the fact that $p>1$![]() and Poincaré-Sobolev inequality on the hyperbolic space.
and Poincaré-Sobolev inequality on the hyperbolic space.
Further, define
Remark 8.2 Clearly, $g(t u)=t^{2}\|u\|_{H_{\lambda }(\mathbb {B}^{N})}^{2}-t^{p+1} p\|a\|_{L^{\infty }(\mathbb {B}^{N})}\|u\|_{L^{p+1}(\mathbb {B}^{N})}^{p+1}$![]() for any $t>0$
for any $t>0$![]() . Moreover, for $u \in H^{1}(\mathbb {B}^{N})$
. Moreover, for $u \in H^{1}(\mathbb {B}^{N})$![]() with $\|u\|_{H_{\lambda }}=1$
with $\|u\|_{H_{\lambda }}=1$![]() , there exists unique $t=t(u)$
, there exists unique $t=t(u)$![]() such that $t u \in U$
such that $t u \in U$![]() . On the other hand, $g(t u)=(t^{2}-t^{p+1})\|u\|_{H_{\lambda }}^{2}$
. On the other hand, $g(t u)=(t^{2}-t^{p+1})\|u\|_{H_{\lambda }}^{2}$![]() for any $u \in U$
for any $u \in U$![]() . Thus
. Thus
Lemma 8.3 The following inequality holds $\forall u \in U$![]() ,
,
where $S_{1,\lambda }$![]() as defined in (3.10) and $C_{p}$
as defined in (3.10) and $C_{p}$![]() as defined in Theorem 1.3.
as defined in Theorem 1.3.
Proof. As $u \in U$![]() , we get $\|u\|_{L^{p+1}}=\frac {\|u\|_{H_{\lambda }(\mathbb {B}^{N})}^{\frac {2}{p+1}}}{(p\|a\|_{L^{\infty }(\mathbb {B}^{N})})^{\frac {1}{p+1}}}.$
, we get $\|u\|_{L^{p+1}}=\frac {\|u\|_{H_{\lambda }(\mathbb {B}^{N})}^{\frac {2}{p+1}}}{(p\|a\|_{L^{\infty }(\mathbb {B}^{N})})^{\frac {1}{p+1}}}.$ This, together with the definition of $S_{1,\lambda }$
This, together with the definition of $S_{1,\lambda }$![]() , gives
, gives

Therefore, for all $u \in U$![]() , we have
, we have

Thus the lemma follows.
Lemma 8.4 Suppose
where $C_{p}$![]() is defined in Theorem 1.3. Then $c_{0}< c_{1}$
is defined in Theorem 1.3. Then $c_{0}< c_{1}$![]() , where $c_{0}$
, where $c_{0}$![]() and $c_{1}$
and $c_{1}$![]() are as defined in (8.1).
are as defined in (8.1).
Proof. Define,
step 1: This step aims to show the existence of a constant $\alpha >0$
 such that
\[ \left.\frac{d}{d t} \tilde{J}(t u)\right|_{t=1} \geq \alpha \quad \forall u \in U . \]It directly follows from the definition of $\tilde {J}$
such that
\[ \left.\frac{d}{d t} \tilde{J}(t u)\right|_{t=1} \geq \alpha \quad \forall u \in U . \]It directly follows from the definition of $\tilde {J}$
 that
\[ \left.\frac{d}{d t} \tilde{J}(t u)\right|_{t=1}=\|u\|_{H_{\lambda}}^{2}-\|a\|_{L^{\infty}\left(\mathbb{B}^{N}\right)}\|u\|_{L^{p+1}\left(\mathbb{B}^{N}\right)}^{p+1}-{\langle f, u\rangle}. \]Therefore, from the definition of $U$
that
\[ \left.\frac{d}{d t} \tilde{J}(t u)\right|_{t=1}=\|u\|_{H_{\lambda}}^{2}-\|a\|_{L^{\infty}\left(\mathbb{B}^{N}\right)}\|u\|_{L^{p+1}\left(\mathbb{B}^{N}\right)}^{p+1}-{\langle f, u\rangle}. \]Therefore, from the definition of $U$
 and substituting the value of $C_{p}$
and substituting the value of $C_{p}$ , we have for $u \in U$
, we have for $u \in U$ (8.4)\begin{equation} \begin{aligned} \left.\frac{d}{d t} \tilde{J}(t u)\right|_{t=1}=\frac{p-1}{p}\|u\|_{H_{\lambda}}^{2}-{\langle f, u\rangle} & =\left(p\|a\|_{L^{\infty}\left(\mathbb{B}^{N}\right)}\right)^{\frac{1}{p-1}} C_{p}\|u\|_{H_{\lambda}}^{2}-\langle f, u\rangle \\ & =\left(\frac{\|u\|_{H_{\lambda}}^{2}}{\|u\|_{L^{p+1}\left(\mathbb{B}^{N}\right)}^{p+1}}\right)^{\frac{1}{p-1}} C_{p}\|u\|_{H_{\lambda}\left(\mathbb{B}^{N}\right)}^{2}\\ & \quad -\langle f, u\rangle =C_{p} \frac{\|u\|_{H_{\lambda}}^{\frac{2p}{p-1}}}{\|u\|_{L^{p+1}\left(\mathbb{B}^{N}\right)}^{\frac{p+1}{p-1}}}-\langle f, u\rangle. \end{aligned} \end{equation}Furthermore, the given hypothesis, i.e., (8.2) implies there exists $d>0$
(8.4)\begin{equation} \begin{aligned} \left.\frac{d}{d t} \tilde{J}(t u)\right|_{t=1}=\frac{p-1}{p}\|u\|_{H_{\lambda}}^{2}-{\langle f, u\rangle} & =\left(p\|a\|_{L^{\infty}\left(\mathbb{B}^{N}\right)}\right)^{\frac{1}{p-1}} C_{p}\|u\|_{H_{\lambda}}^{2}-\langle f, u\rangle \\ & =\left(\frac{\|u\|_{H_{\lambda}}^{2}}{\|u\|_{L^{p+1}\left(\mathbb{B}^{N}\right)}^{p+1}}\right)^{\frac{1}{p-1}} C_{p}\|u\|_{H_{\lambda}\left(\mathbb{B}^{N}\right)}^{2}\\ & \quad -\langle f, u\rangle =C_{p} \frac{\|u\|_{H_{\lambda}}^{\frac{2p}{p-1}}}{\|u\|_{L^{p+1}\left(\mathbb{B}^{N}\right)}^{\frac{p+1}{p-1}}}-\langle f, u\rangle. \end{aligned} \end{equation}Furthermore, the given hypothesis, i.e., (8.2) implies there exists $d>0$
 such that
(8.5)\begin{equation} \inf _{u \in H^{1}\left(\mathbb{B}^{N}\right),\|u\|_{L^{p+1}\left(\mathbb{B}^{N}\right)=1}}\left\{C_{p}\|u\|_{H_{\lambda}}^{\frac{2 p}{p-1}}-\langle f, u\rangle\right\} \geq d . \end{equation}Now,
such that
(8.5)\begin{equation} \inf _{u \in H^{1}\left(\mathbb{B}^{N}\right),\|u\|_{L^{p+1}\left(\mathbb{B}^{N}\right)=1}}\left\{C_{p}\|u\|_{H_{\lambda}}^{\frac{2 p}{p-1}}-\langle f, u\rangle\right\} \geq d . \end{equation}Now, \begin{align*} (8.5) & \Longleftrightarrow C_{p} \frac{\|u\|_{H_{\lambda}\left(\mathbb{B}^{N}\right)}^{\frac{2 p}{p-1}}}{\|u\|_{L^{p+1}\left(\mathbb{B}^{N}\right)}^{\frac{p+1}{p-1}}}-\langle f, u\rangle \geq d, \quad\|u\|_{L^{p+1}\left(\mathbb{B}^{N}\right)}=1\\ & \Longleftrightarrow C_{p} \frac{\|u\|_{H_{\lambda}\left(\mathbb{B}^{N}\right)}^{\frac{2 p}{p-1}}}{\|u\|_{L^{p+1}\left(\mathbb{B}^{N}\right)}^{\frac{p+1}{p-1}}}-\langle f, u\rangle \geq d\|u\|_{L^{p+1}\left(\mathbb{B}^{N}\right)}, \quad u \in H^{1}\left(\mathbb{B}^{N}\right) \backslash\{0\} . \end{align*}
\begin{align*} (8.5) & \Longleftrightarrow C_{p} \frac{\|u\|_{H_{\lambda}\left(\mathbb{B}^{N}\right)}^{\frac{2 p}{p-1}}}{\|u\|_{L^{p+1}\left(\mathbb{B}^{N}\right)}^{\frac{p+1}{p-1}}}-\langle f, u\rangle \geq d, \quad\|u\|_{L^{p+1}\left(\mathbb{B}^{N}\right)}=1\\ & \Longleftrightarrow C_{p} \frac{\|u\|_{H_{\lambda}\left(\mathbb{B}^{N}\right)}^{\frac{2 p}{p-1}}}{\|u\|_{L^{p+1}\left(\mathbb{B}^{N}\right)}^{\frac{p+1}{p-1}}}-\langle f, u\rangle \geq d\|u\|_{L^{p+1}\left(\mathbb{B}^{N}\right)}, \quad u \in H^{1}\left(\mathbb{B}^{N}\right) \backslash\{0\} . \end{align*}
Hence, step 1 follows by using the above estimate in (8.4) and by Remark (8.1).
Step 2 Let $u_{n}$
 be a minimizing sequence for $I_{\lambda,a, f}$
be a minimizing sequence for $I_{\lambda,a, f}$ on $U$
on $U$ , i.e.,
, i.e.,$I_{\lambda,a, f}(u_{n}) \rightarrow c_{1}$
 and $\left \|u_{n}\right \|_{H_{\lambda }}^{2}=p\|a\|_{L^{\infty }(\mathbb {B}^{N})}\left \|u_{n}\right \|_{L^{p+1}(\mathbb {B}^{N})}^{p+1}$
and $\left \|u_{n}\right \|_{H_{\lambda }}^{2}=p\|a\|_{L^{\infty }(\mathbb {B}^{N})}\left \|u_{n}\right \|_{L^{p+1}(\mathbb {B}^{N})}^{p+1}$ . Thus for $n$
. Thus for $n$ large, we get
\begin{align*} & c_{1}+o(1) \geq I_{\lambda,a, f}\left(u_{n}\right) \geq \tilde{J}\left(u_{n}\right) \geq\left(\frac{1}{2}-\frac{1}{p(p+1)}\right)\left\|u_{n}\right\|_{H_{\lambda}}^{2}\\ & \quad -\|f\|_{H^{{-}1}\left(\mathbb{B}^{N}\right)}\left\|u_{n}\right\|_{H_{\lambda}} . \end{align*}As a result, $\left \{\tilde {J}(u_{n})\right \}$
large, we get
\begin{align*} & c_{1}+o(1) \geq I_{\lambda,a, f}\left(u_{n}\right) \geq \tilde{J}\left(u_{n}\right) \geq\left(\frac{1}{2}-\frac{1}{p(p+1)}\right)\left\|u_{n}\right\|_{H_{\lambda}}^{2}\\ & \quad -\|f\|_{H^{{-}1}\left(\mathbb{B}^{N}\right)}\left\|u_{n}\right\|_{H_{\lambda}} . \end{align*}As a result, $\left \{\tilde {J}(u_{n})\right \}$
 is a bounded sequence. Also, $\left \|u_{n}\right \|_{H_{\lambda }}$
is a bounded sequence. Also, $\left \|u_{n}\right \|_{H_{\lambda }}$ and $\left \|u_{n}\right \|_{L^{p+1}(\mathbb {B}^{N})}$
and $\left \|u_{n}\right \|_{L^{p+1}(\mathbb {B}^{N})}$ are bounded.
are bounded.
Claim: $c_{0}<0$
 .
.To prove the above claim, it suffices to show that there exists $v \in U_{1}$
 such that $I_{\lambda,a, f}(v)<0$
such that $I_{\lambda,a, f}(v)<0$ . Remark (8.2) implies we can choose $u \in U$
. Remark (8.2) implies we can choose $u \in U$ such that $\langle f,\, u\rangle >0$
such that $\langle f,\, u\rangle >0$ . Therefore,
\[ I_{\lambda,a, f}(t u) \leq t^{2}\|u\|_{L^{p+1}\left(\mathbb{B}^{N}\right)}^{p+1}\left[\frac{p\|a\|_{L^{\infty}\left(\mathbb{B}^{N}\right)}}{2}-\frac{t^{p-1}}{p+1}\right]-t\langle f, u\rangle<0 . \]for $t<<1$
. Therefore,
\[ I_{\lambda,a, f}(t u) \leq t^{2}\|u\|_{L^{p+1}\left(\mathbb{B}^{N}\right)}^{p+1}\left[\frac{p\|a\|_{L^{\infty}\left(\mathbb{B}^{N}\right)}}{2}-\frac{t^{p-1}}{p+1}\right]-t\langle f, u\rangle<0 . \]for $t<<1$
 . Moreover, by Remark (8.2), $t u \in U_{1}$
. Moreover, by Remark (8.2), $t u \in U_{1}$ . This proves the claim.
. This proves the claim.
Now $I_{\lambda, a, f}(u_{n})<0$
 for large $n$
for large $n$ by using the above claim. Consequently,
\[ 0>I_{\lambda,a, f}\left(u_{n}\right) \geq\left(\frac{1}{2}-\frac{1}{p(p+1)}\right)\left\|u_{n}\right\|_{H_{\lambda}}^{2}-\left\langle f, u_{n}\right\rangle. \]Therefore, $p>1$
by using the above claim. Consequently,
\[ 0>I_{\lambda,a, f}\left(u_{n}\right) \geq\left(\frac{1}{2}-\frac{1}{p(p+1)}\right)\left\|u_{n}\right\|_{H_{\lambda}}^{2}-\left\langle f, u_{n}\right\rangle. \]Therefore, $p>1$
 implies $\left \langle f,\, u_{n}\right \rangle >0$
implies $\left \langle f,\, u_{n}\right \rangle >0$ for all large $n$
for all large $n$ . As a a result, $\frac {d}{d t} \tilde {J}(t u_{n})<0$
. As a a result, $\frac {d}{d t} \tilde {J}(t u_{n})<0$ for $t>0$
for $t>0$ small enough. Thus, by Step 1, there exists $t_{n} \in (0,\,1)$
small enough. Thus, by Step 1, there exists $t_{n} \in (0,\,1)$ such that $\frac {d}{d t} \tilde {J}(t_{n} u_{n})=0$
such that $\frac {d}{d t} \tilde {J}(t_{n} u_{n})=0$ . In addition, $t_{n}$
. In addition, $t_{n}$ is unique because
\begin{align*} \frac{d^{2}}{d t^{2}} \tilde{J}(t u)& =\|u\|_{H_{\lambda}}^{2}-p\|a\|_{L^{\infty}\left(\mathbb{B}^{N}\right)} t^{p-1}\|u\|_{L^{p+1}\left(\mathbb{B}^{N}\right)}^{p+1}\\ & =\left(1-t^{p-1}\right)\|u\|_{H_{\lambda}}^{2}>0, \;\forall u \in U,\; \forall t \in[0,1) . \end{align*}
is unique because
\begin{align*} \frac{d^{2}}{d t^{2}} \tilde{J}(t u)& =\|u\|_{H_{\lambda}}^{2}-p\|a\|_{L^{\infty}\left(\mathbb{B}^{N}\right)} t^{p-1}\|u\|_{L^{p+1}\left(\mathbb{B}^{N}\right)}^{p+1}\\ & =\left(1-t^{p-1}\right)\|u\|_{H_{\lambda}}^{2}>0, \;\forall u \in U,\; \forall t \in[0,1) . \end{align*}
Step 3 The goal of this step is to prove the following
(8.6)\begin{equation} \liminf _{n \rightarrow \infty}\left\{\tilde{J}\left(u_{n}\right)-\tilde{J}\left(t_{n} u_{n}\right)\right\}>0. \end{equation}We can notice that $\tilde {J}(u_{n})-\tilde {J}(t_{n} u_{n})=\int _{t_{n}}^{1} \frac {d}{d t}\left \{\tilde {J}(t u_{n})\right \} \mathrm {d} t$
 and that for all $n \in \mathbb {N}$
and that for all $n \in \mathbb {N}$ , there is $\xi _{n}>0$
, there is $\xi _{n}>0$ such that $t_{n} \in (0,\,1-2 \xi _{n})$
such that $t_{n} \in (0,\,1-2 \xi _{n})$ and $\frac {d}{d t} \tilde {J}(t u_{n}) \geq \alpha$
and $\frac {d}{d t} \tilde {J}(t u_{n}) \geq \alpha$ for $t \in [1-\xi _{n},\, 1]$
for $t \in [1-\xi _{n},\, 1]$ .
.
To prove (8.6), it is enough to show that $\xi _{n}>0$
 can be chosen independently of $n \in \mathbb {N}$
can be chosen independently of $n \in \mathbb {N}$ . But this is true because, by step 1, we have $\left.\frac {d}{d t} \tilde {J}(t u_{n})\right |_{t=1} \geq \alpha$
. But this is true because, by step 1, we have $\left.\frac {d}{d t} \tilde {J}(t u_{n})\right |_{t=1} \geq \alpha$ . Moreover, the boundedness of $\left \{u_{n}\right \}$
. Moreover, the boundedness of $\left \{u_{n}\right \}$ gives
\begin{align*} \left|{\frac{d^{2}}{d t^{2}} \tilde{J}\left(t u_{n}\right)}\right|& =\left|\left\|u_{n}\right\|_{H_{\lambda}\left(\mathbb{B}^{N}\right)}^{2}-p\|a\|_{L^{\infty}\left(\mathbb{B}^{N}\right)} t^{p-1}\left\|u_{n}\right\|_{L^{p+1}\left(\mathbb{B}^{N}\right)}^{p+1}\right|\\ & \quad =\left|\left(1-t^{p-1}\right)\left\|u_{n}\right\|_{H_{\lambda}}^{2}\right|\leq C, \end{align*}for all $n \geq 1$
gives
\begin{align*} \left|{\frac{d^{2}}{d t^{2}} \tilde{J}\left(t u_{n}\right)}\right|& =\left|\left\|u_{n}\right\|_{H_{\lambda}\left(\mathbb{B}^{N}\right)}^{2}-p\|a\|_{L^{\infty}\left(\mathbb{B}^{N}\right)} t^{p-1}\left\|u_{n}\right\|_{L^{p+1}\left(\mathbb{B}^{N}\right)}^{p+1}\right|\\ & \quad =\left|\left(1-t^{p-1}\right)\left\|u_{n}\right\|_{H_{\lambda}}^{2}\right|\leq C, \end{align*}for all $n \geq 1$
 and $t \in [0,\,1]$
and $t \in [0,\,1]$ .
.Step 4 It straight away follows from the definition of $I_{\lambda,a, f}$
 and $\tilde {J}$
and $\tilde {J}$ that $\frac {d}{d t} I_{\lambda,a, f}(t u) \geq \frac {d}{d t} \tilde {J}(t u)$
that $\frac {d}{d t} I_{\lambda,a, f}(t u) \geq \frac {d}{d t} \tilde {J}(t u)$ for all $u \in H^{1}(\mathbb {B}^{N})$
for all $u \in H^{1}(\mathbb {B}^{N})$ and for all $t>0$
and for all $t>0$ . Therefore,
\begin{align*} I_{\lambda,a, f}\left(u_{n}\right)-I_{\lambda,a, f}\left(t_{n} u_{n}\right)& =\int_{t_{n}}^{1} \frac{d}{d t}\left(I_{\lambda,a, f}\left(t u_{n}\right)\right) \mathrm{d} t \geq \int_{t_{n}}^{1} \frac{d}{d t} \tilde{J}\left(t u_{n}\right) \mathrm{d} t\\ & =\tilde{J}\left(u_{n}\right)-\tilde{J}\left(t_{n} u_{n}\right). \end{align*}Since $\left \{u_{n}\right \} \in U$
. Therefore,
\begin{align*} I_{\lambda,a, f}\left(u_{n}\right)-I_{\lambda,a, f}\left(t_{n} u_{n}\right)& =\int_{t_{n}}^{1} \frac{d}{d t}\left(I_{\lambda,a, f}\left(t u_{n}\right)\right) \mathrm{d} t \geq \int_{t_{n}}^{1} \frac{d}{d t} \tilde{J}\left(t u_{n}\right) \mathrm{d} t\\ & =\tilde{J}\left(u_{n}\right)-\tilde{J}\left(t_{n} u_{n}\right). \end{align*}Since $\left \{u_{n}\right \} \in U$
 is a minimizing sequence for $I_{\lambda, a, f}$
is a minimizing sequence for $I_{\lambda, a, f}$ , and $t_{n} u_{n} \in U_{1}$
, and $t_{n} u_{n} \in U_{1}$ , we deduce using (8.6) that
\[ c_{0}=\inf _{u \in U_{1}} I_{\lambda,a, f}(u)<\inf _{u \in U} I_{\lambda,a, f}(u) = c_{1} \]
, we deduce using (8.6) that
\[ c_{0}=\inf _{u \in U_{1}} I_{\lambda,a, f}(u)<\inf _{u \in U} I_{\lambda,a, f}(u) = c_{1} \]
This completes the proof of the lemma.
It is worth mentioning explicitly the problem at infinity corresponding to (3.4) :
and the associated functional $I_{\lambda,1,0}: H^{1}(\mathbb {B}^{N}) \rightarrow \mathbb {R}$![]() defined by
defined by
Define,
Remark 8.5 We can easily see $I_{\lambda,1,0}(u)=\frac {p-1}{2(p+1)}\|u\|_{H_{\lambda }}^{2}$![]() on $X_{1}$
on $X_{1}$![]() . Further,(3.10) also gives $\|u\|_{H_{\lambda }}^{2} \geq S_{1,\lambda }^{\frac {p+1}{p-1}}$
. Further,(3.10) also gives $\|u\|_{H_{\lambda }}^{2} \geq S_{1,\lambda }^{\frac {p+1}{p-1}}$![]() on $X_{1}$
on $X_{1}$![]() . Consequently, $S^{\infty } \geq$
. Consequently, $S^{\infty } \geq$![]() $\frac {p-1}{2(p+1)} S_{1,\lambda }^{\frac {p+1}{p-1}}>0$
$\frac {p-1}{2(p+1)} S_{1,\lambda }^{\frac {p+1}{p-1}}>0$![]() . Moreover, it is known from [Reference Mancini and Sandeep29] that $S_{1,\lambda }$
. Moreover, it is known from [Reference Mancini and Sandeep29] that $S_{1,\lambda }$![]() is achieved by unique positive radial solution $w$
is achieved by unique positive radial solution $w$![]() of (3.1). Therefore,
of (3.1). Therefore,
Thus $S^{\infty }$![]() is achieved by $w$
is achieved by $w$![]() .
.
Proposition 8.6 Suppose (8.2) and all the assumptions in the Theorem 1.3 hold. Then there exists a critical point $u_{0} \in U_{1}$![]() of $I_{\lambda,a, f}$
of $I_{\lambda,a, f}$![]() such that $I_{\lambda,a, f}(u_{0})=c_{0}$
such that $I_{\lambda,a, f}(u_{0})=c_{0}$![]() . In particular, $u_{0}$
. In particular, $u_{0}$![]() is a weak positive solution to ($\mathcal {P}$
is a weak positive solution to ($\mathcal {P}$![]() ).
).
Proof. We divide the proof into the following few steps.
Step 1 $c_{0}>-\infty.$

As $I_{\lambda,a, f}(u) \geq \tilde {J}(u)$
 so, to prove Step 1, it is enough to show that $\tilde {J}$
so, to prove Step 1, it is enough to show that $\tilde {J}$ is bounded from below. The definition of $U_{1}$
is bounded from below. The definition of $U_{1}$ implies
(8.9)\begin{equation} \tilde{J}(u) \geq\left[\frac{1}{2}-\frac{1}{p(p+1)}\right]\|u\|_{H_{\lambda}}^{2}-\|f\|_{H^{{-}1}\left(\mathbb{B}^{N}\right)}\|u\|_{H_{\lambda}} \text{ for all } u \in U_{1} . \end{equation}Since the RHS of the above inequality is a quadratic function in $\|u\|_{H_{\lambda }}$
implies
(8.9)\begin{equation} \tilde{J}(u) \geq\left[\frac{1}{2}-\frac{1}{p(p+1)}\right]\|u\|_{H_{\lambda}}^{2}-\|f\|_{H^{{-}1}\left(\mathbb{B}^{N}\right)}\|u\|_{H_{\lambda}} \text{ for all } u \in U_{1} . \end{equation}Since the RHS of the above inequality is a quadratic function in $\|u\|_{H_{\lambda }}$
 implies $\tilde {J}$
implies $\tilde {J}$ is bounded from below. Hence Step 1 follows.
is bounded from below. Hence Step 1 follows.Step 2 We aim to find a bounded PS sequence $\left \{u_{n}\right \} \subset U_{1}$
 for $I_{\lambda,a,f}$
for $I_{\lambda,a,f}$ at the level $c_{0}$
at the level $c_{0}$ .
.Let $\left \{u_{n}\right \} \subset \bar {U}_{1}$
 such that $I_{\lambda, a, f}(u_{n}) \rightarrow c_{0}$
such that $I_{\lambda, a, f}(u_{n}) \rightarrow c_{0}$ . As $I_{\lambda,a, f}(u) \geq \tilde {J}(u)$
. As $I_{\lambda,a, f}(u) \geq \tilde {J}(u)$ so, from (8.9), we get $\left \{u_{n}\right \}$
so, from (8.9), we get $\left \{u_{n}\right \}$ is a bounded sequence. Since by Lemma 8.4, $c_{0}< c_{1}$
is a bounded sequence. Since by Lemma 8.4, $c_{0}< c_{1}$ , without restriction we can assume $u_{n} \in U_{1}$
, without restriction we can assume $u_{n} \in U_{1}$ . Therefore, by Ekeland's variational principle, we can extract a PS sequence from $\left \{u_{n}\right \}$
. Therefore, by Ekeland's variational principle, we can extract a PS sequence from $\left \{u_{n}\right \}$ in $U_{1}$
in $U_{1}$ for $I_{\lambda,a, f}$
for $I_{\lambda,a, f}$ at the level $c_{0}$
at the level $c_{0}$ . We still denote this PS sequence by $\left \{u_{n}\right \}$
. We still denote this PS sequence by $\left \{u_{n}\right \}$ . Thus step 2 follows.
. Thus step 2 follows.Step 3 In this step, we show that there exists $u_{0} \in U_{1}$
 such that $u_{n} \rightarrow u_{0}$
such that $u_{n} \rightarrow u_{0}$ in $H^{1}(\mathbb {B}^{N})$
in $H^{1}(\mathbb {B}^{N})$ .
.Applying PS decomposition (4) gives
(8.10)\begin{equation} u_{n}-u_{0}-\sum_{i=1}^{m} w^{i}\left(\tau_{n}^{i}(x)\right) \rightarrow 0 \text{ in } H^{1}\left(\mathbb{B}^{N}\right) \end{equation}for some $u_{0}$
 such that $(I_{\lambda,a, f})^{\prime }(u_{0})=0$
such that $(I_{\lambda,a, f})^{\prime }(u_{0})=0$ and some appropriate $w^{i}$
and some appropriate $w^{i}$ and $\left \{\tau _{n}^{i}\right \}$
and $\left \{\tau _{n}^{i}\right \}$ . We will proceed by the method of contradiction to show that $m=0$
. We will proceed by the method of contradiction to show that $m=0$ , which in turn will imply step 3. Assume that there is $w^{i} \neq 0$
, which in turn will imply step 3. Assume that there is $w^{i} \neq 0$ for $i \in \{1,\,2,\, \cdots,\, m\}$
for $i \in \{1,\,2,\, \cdots,\, m\}$ such that $(I_{\lambda,1,0})^{\prime }(w^{i})=0$
such that $(I_{\lambda,1,0})^{\prime }(w^{i})=0$ , i.e, $\left \|w^{i}\right \|_{H_{\lambda }}^{2}=\int _{\mathbb {B}^{N}}(w^{i})_+^{p+1} \mathrm {~d}V_{\mathbb {B}^{N}}$
, i.e, $\left \|w^{i}\right \|_{H_{\lambda }}^{2}=\int _{\mathbb {B}^{N}}(w^{i})_+^{p+1} \mathrm {~d}V_{\mathbb {B}^{N}}$ . Therefore,
\begin{align*} g\left(w^{i}\right)& =\left\|w^{i}\right\|_{H_{\lambda}}^{2}-p\|a\|_{L^{\infty}\left(\mathbb{B}^{N}\right)}\left\|w^{i}\right\|_{L^{p+1}\left(\mathbb{B}^{N}\right)}^{p+1}\\ & =\int_{\mathbb{B}^{N}}\left(w^{i}\right)_+^{p+1} \mathrm{~d}V_{\mathbb{B}^{N}}-p\|a\|_{L^{\infty}\left(\mathbb{B}^{N}\right)} \int_{\mathbb{B}^{N}}\left|w^{i}\right|^{p+1} \mathrm{~d}V_{\mathbb{B}^{N}} \\ & \leq\left\|w^{i}\right\|_{L^{p+1}\left(\mathbb{B}^{N}\right)}^{p+1}\left(1-p\|a\|_{L^{\infty}\left(\mathbb{B}^{N}\right)}\right)<0, \end{align*}where for the last inequality, we have used that $p>1$
. Therefore,
\begin{align*} g\left(w^{i}\right)& =\left\|w^{i}\right\|_{H_{\lambda}}^{2}-p\|a\|_{L^{\infty}\left(\mathbb{B}^{N}\right)}\left\|w^{i}\right\|_{L^{p+1}\left(\mathbb{B}^{N}\right)}^{p+1}\\ & =\int_{\mathbb{B}^{N}}\left(w^{i}\right)_+^{p+1} \mathrm{~d}V_{\mathbb{B}^{N}}-p\|a\|_{L^{\infty}\left(\mathbb{B}^{N}\right)} \int_{\mathbb{B}^{N}}\left|w^{i}\right|^{p+1} \mathrm{~d}V_{\mathbb{B}^{N}} \\ & \leq\left\|w^{i}\right\|_{L^{p+1}\left(\mathbb{B}^{N}\right)}^{p+1}\left(1-p\|a\|_{L^{\infty}\left(\mathbb{B}^{N}\right)}\right)<0, \end{align*}where for the last inequality, we have used that $p>1$
 and $\|a\|_{L^{\infty }(\mathbb {B}^{N})} \geq 1$
and $\|a\|_{L^{\infty }(\mathbb {B}^{N})} \geq 1$ . Further, using the Remark 8.5, we get $I_{\lambda,1,0}(w^{i}) \geq S^{\infty }>0$
. Further, using the Remark 8.5, we get $I_{\lambda,1,0}(w^{i}) \geq S^{\infty }>0$ for all $1 \leq i \leq m$
for all $1 \leq i \leq m$ . Therefore, $I_{\lambda,a, f}(u_{n}) \rightarrow I_{\lambda,a, f}(u_{0})+\sum _{i=1}^{m} I_{\lambda,1,0}(w_{i})$
. Therefore, $I_{\lambda,a, f}(u_{n}) \rightarrow I_{\lambda,a, f}(u_{0})+\sum _{i=1}^{m} I_{\lambda,1,0}(w_{i})$ implies $I_{\lambda,a, f}(u_{0})< c_{0}$
implies $I_{\lambda,a, f}(u_{0})< c_{0}$ . Thus $u_{0} \notin U_{1}$
. Thus $u_{0} \notin U_{1}$ , i.e., $g(u_{0}) \leq 0 .$
, i.e., $g(u_{0}) \leq 0 .$
We have $g(u_{n}) \geq 0$
 because $u_{n} \in U_{1}$
because $u_{n} \in U_{1}$ . We now compute $g(u_{0}+\sum _{i=1}^{m} w^{i}(\tau _{n}^{i}(x)))$
. We now compute $g(u_{0}+\sum _{i=1}^{m} w^{i}(\tau _{n}^{i}(x)))$ . Thus (8.10) and uniform continuity of $g$
. Thus (8.10) and uniform continuity of $g$ implies
(8.11)\begin{equation} 0 \leq \liminf _{n \rightarrow \infty} g\left(u_{n}\right)=\liminf _{n \rightarrow \infty} g\left(u_{0}+\sum_{i=1}^{m} w^{i}\left(\tau_{n}^{i}(x)\right)\right).\end{equation}On the other hand, as $\tau _{n}^{i}(0) \rightarrow \infty,\,\; d(\tau _{n}^{i}(0),\,\tau _{n}^{j}(0))\rightarrow \infty$
implies
(8.11)\begin{equation} 0 \leq \liminf _{n \rightarrow \infty} g\left(u_{n}\right)=\liminf _{n \rightarrow \infty} g\left(u_{0}+\sum_{i=1}^{m} w^{i}\left(\tau_{n}^{i}(x)\right)\right).\end{equation}On the other hand, as $\tau _{n}^{i}(0) \rightarrow \infty,\,\; d(\tau _{n}^{i}(0),\,\tau _{n}^{j}(0))\rightarrow \infty$
 for $1 \leq i \neq j \leq m$
for $1 \leq i \neq j \leq m$ the supports of $u_{0}(\bullet )$
the supports of $u_{0}(\bullet )$ and $w^{i}(\tau _{n}^{i}(\bullet ))$
and $w^{i}(\tau _{n}^{i}(\bullet ))$ are going increasingly far away as $n \rightarrow \infty$
are going increasingly far away as $n \rightarrow \infty$ . Therefore,
\begin{align*} & \lim _{n \rightarrow \infty} g\left(u_{0}+\sum_{i=1}^{m} w^{i}\left(\tau_{n}^{i}(x)\right)\right)=g\left(u_{0}\right)\\ & \quad +\lim _{n \rightarrow \infty} \sum_{i=1}^{m} g\left(w^{i}\left(\tau_{n}^{i}(x)\right)\right)=g\left(u_{0}\right)+\sum_{i=1}^{m} g\left(w^{i}\right), \end{align*}where the last equality follows from the translation invariance of $g$
. Therefore,
\begin{align*} & \lim _{n \rightarrow \infty} g\left(u_{0}+\sum_{i=1}^{m} w^{i}\left(\tau_{n}^{i}(x)\right)\right)=g\left(u_{0}\right)\\ & \quad +\lim _{n \rightarrow \infty} \sum_{i=1}^{m} g\left(w^{i}\left(\tau_{n}^{i}(x)\right)\right)=g\left(u_{0}\right)+\sum_{i=1}^{m} g\left(w^{i}\right), \end{align*}where the last equality follows from the translation invariance of $g$
 . Now because $g(u_{0}) \leq 0$
. Now because $g(u_{0}) \leq 0$ and $g(w^{i})<0$
and $g(w^{i})<0$ for $1\leq i \leq m$
for $1\leq i \leq m$ , we get a contradiction to (8.11). This proves step 3.
, we get a contradiction to (8.11). This proves step 3.Step 4 Using the previous steps, we can conclude that $I_{\lambda,a, f}(u_{0})=c_{0}$
 and $(I_{\lambda,a, f})^{\prime }(u_{0})=0$
and $(I_{\lambda,a, f})^{\prime }(u_{0})=0$ . Thus, $u_{0}$
. Thus, $u_{0}$ is a weak solution to (3.4); combining this with Remark 3.1, we complete the proof of the proposition.
is a weak solution to (3.4); combining this with Remark 3.1, we complete the proof of the proposition.
Proposition 8.7 Assume (8.2) holds. Then $I_{\lambda,a, f}$![]() has a second critical point $v_{0} \neq u_{0}$
has a second critical point $v_{0} \neq u_{0}$![]() . In particular, $v_{0}$
. In particular, $v_{0}$![]() is a positive solution to ($\mathcal {P}$
is a positive solution to ($\mathcal {P}$![]() ).
).
Proof. For $u_{0}$![]() to be the critical point found in Proposition 8.6 and $w$
to be the critical point found in Proposition 8.6 and $w$![]() to be as in Remark 8.5, set $w_{t}(x):=t w(x).$
to be as in Remark 8.5, set $w_{t}(x):=t w(x).$![]()
Claim 1: $u_{0}+w_{t} \in U_{2}$![]() for $t>0$
for $t>0$![]() large enough.
large enough.
As $p>1$![]() and $\|a\|_{L^{\infty }(\mathbb {B}^{N})} \geq 1$
and $\|a\|_{L^{\infty }(\mathbb {B}^{N})} \geq 1$![]() , we have
, we have

where the second last step follows from Young's inequality with $\varepsilon >0$![]() . Moreover, as $w$
. Moreover, as $w$![]() is the solution to (3.1) implies
is the solution to (3.1) implies
Finally,
Thus choosing $\varepsilon >0$![]() such that $1+\varepsilon < p$
such that $1+\varepsilon < p$![]() gives $g(u_{0}+w_{t})<0$
gives $g(u_{0}+w_{t})<0$![]() for $t>0$
for $t>0$![]() large enough. Hence the claim follows.
large enough. Hence the claim follows.
Claim 2: $I_{\lambda,a, f}(u_{0}+w_{t})< I_{\lambda,a, f}(u_{0})+I_{\lambda,1,0}(w_{t}) \forall t>0$![]() .
.
As $u_{0},\, w_{t}>0$![]() , using $w_{t}$
, using $w_{t}$![]() as the test function for (3.4) yields
as the test function for (3.4) yields
Therefore, utilizing the above expression and assumption $a \geq 1$![]() , we compute the following
, we compute the following

This proves the claim. Further, the straightforward calculation gives
From (8.12) and Remark 8.5, we have
Combing this with Claim 2 yields
Claim 2, together with (8.12), results in
We now fix $t_{0}>0$![]() large enough such that (8.14) and Claim 1 are satisfied. Then set
large enough such that (8.14) and Claim 1 are satisfied. Then set
where
As $u_{0} \in U_{1}$![]() and $u_{0}+w_{t_{0}} \in U_{2}$
and $u_{0}+w_{t_{0}} \in U_{2}$![]() , for every $i \in \Gamma$
, for every $i \in \Gamma$![]() , there exists $t_{i} \in (0,\,1)$
, there exists $t_{i} \in (0,\,1)$![]() such that $i(t_{i}) \in U$
such that $i(t_{i}) \in U$![]() . Therefore,
. Therefore,
Thus, using Lemma 8.4, we have $\gamma \geq c_{1}>c_{0}=I_{\lambda,a, f}(u_{0})$![]() .
.
Claim 3: For $S^{\infty }$![]() , as defined in (8.8), $\gamma < I_{\lambda,a, f}(u_{0})+S^{\infty }$
, as defined in (8.8), $\gamma < I_{\lambda,a, f}(u_{0})+S^{\infty }$![]() .
.
Observe that $\lim _{t \rightarrow 0}\left \|w_{t}\right \|_{H_{\lambda }}=0$![]() . Thus, if we define $\tilde {i}(t)=u_{0}+w_{tt_{0}}$
. Thus, if we define $\tilde {i}(t)=u_{0}+w_{tt_{0}}$![]() ,
,
then $\lim _{t \rightarrow 0}\left \|\tilde {i}(t)-u_{0}\right \|_{H_{\lambda }}=0$![]() . As a result, $\tilde {i} \in \Gamma$
. As a result, $\tilde {i} \in \Gamma$![]() . Therefore, using (8.13) will give us
. Therefore, using (8.13) will give us
Hence the claim follows. Thus
Applying Ekeland's variational principle, there exists a PS sequence $\left \{u_{n}\right \}$![]() for $I_{\lambda,a, f}$
for $I_{\lambda,a, f}$![]() at the level $\gamma$
at the level $\gamma$![]() . Also, note that $\left \{u_{n}\right \}$
. Also, note that $\left \{u_{n}\right \}$![]() is a bounded sequence. Further, from PS decomposition and Remark (8.5), we have $S^{\infty }=I_{\lambda,1,0}(w)$
is a bounded sequence. Further, from PS decomposition and Remark (8.5), we have $S^{\infty }=I_{\lambda,1,0}(w)$![]() and $u_{n} \rightarrow v_{0}$
and $u_{n} \rightarrow v_{0}$![]() for some $v_{0} \in H^{1}(\mathbb {B}^{N})$
for some $v_{0} \in H^{1}(\mathbb {B}^{N})$![]() such that $(I_{\lambda,a, f})^{\prime }(v_{0})=0$
such that $(I_{\lambda,a, f})^{\prime }(v_{0})=0$![]() and $I_{\lambda,a, f}(v_{0})=\gamma$
and $I_{\lambda,a, f}(v_{0})=\gamma$![]() . Further, as $I_{\lambda,a, f}(u_{0})<\gamma$
. Further, as $I_{\lambda,a, f}(u_{0})<\gamma$![]() , we conclude $v_{0} \neq u_{0}$
, we conclude $v_{0} \neq u_{0}$![]() . Finally, $(I_{\lambda,a, f})^{\prime }(v_{0})=0$
. Finally, $(I_{\lambda,a, f})^{\prime }(v_{0})=0$![]() , along with the Remark 3.1, completes the proof of the proposition.
, along with the Remark 3.1, completes the proof of the proposition.
Lemma 8.8 If $\|f\|_{H^{-1}(\mathbb {B}^{N})}< C_{p} S_{1,\lambda }^{\frac {p+1}{2(p-1)}}$![]() , then (8.2) holds.
, then (8.2) holds.
Proof. We can find an $\varepsilon >0$![]() such that $\|f\|_{H^{-1}(\mathbb {B}^{N})}< C_{p} S_{1,\lambda }^{\frac {p+1}{2(p-1)}}-\varepsilon$
such that $\|f\|_{H^{-1}(\mathbb {B}^{N})}< C_{p} S_{1,\lambda }^{\frac {p+1}{2(p-1)}}-\varepsilon$![]() using the given assumption. Therefore, using Lemma 8.3. we have
using the given assumption. Therefore, using Lemma 8.3. we have

Thus
Moreover, Remark 8.1 gives us that $\|u\|_{H_{\lambda }}$![]() is bounded away from 0 on $U$
is bounded away from 0 on $U$![]() , so the above expression yields
, so the above expression yields
On the other hand,

Hence the lemma follows.
Combining Proposition 8.6 and Proposition 8.7 with Lemma 8.8, we conclude the proof of Theorem 1.3.
Acknowledgements
D. Ganguly is partially supported by the INSPIRE faculty fellowship (IFA17-MA98). D. Gupta is supported by the PMRF fellowship.
Conflict of interest
The authors declare that they have no conflict of interest.