No CrossRef data available.
Article contents
Multiple solutions for some classes of non-linear elliptic equations with variable exponents
Published online by Cambridge University Press: 24 February 2025
Abstract
This article concerns the existence and multiplicity of solutions for the following class of non-linear elliptic equations with variable exponents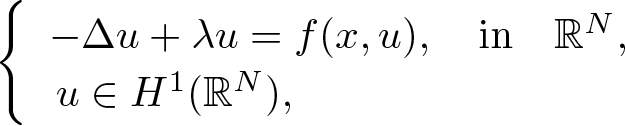
\begin{equation*}\left\{\begin{array}{l}-\Delta u+\lambda u=f(x,u), \quad \text{in} \quad \mathbb{R}^N, \\\,u\in H^{1}(\mathbb{R}^N),\\\end{array}\right.\end{equation*}
where λ > 0,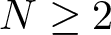 
$N\geq 2$ and 
$f:\mathbb{R}^N \times \mathbb{R} \to \mathbb{R}$ is a function of the following types:
Type 1: The subcritical case: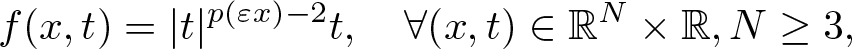
\begin{equation*}f(x,t)=|t|^{p(\varepsilon x)-2}t, \quad \forall (x,t) \in \mathbb{R}^N\times \mathbb{R}, N\geq3, \end{equation*}
Type 2: The critical case: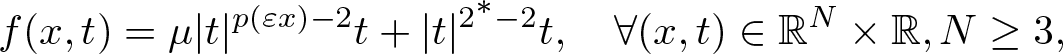
\begin{equation*}f(x,t)=\mu|t|^{p(\varepsilon x)-2}t+|t|^{2^*-2}t, \quad \forall (x,t) \in \mathbb{R}^N\times \mathbb{R}, N\geq3, \end{equation*}
Type 3: The exponential subcritical growth case: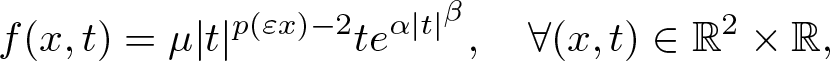
\begin{equation*} f(x,t)=\mu|t|^{p(\varepsilon x)-2}te^{\alpha|t|^\beta}, \quad \forall (x,t) \in \mathbb{R}^2\times \mathbb{R}, \end{equation*}
where parameterɛ > 0, α > 0,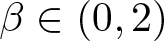 
$\beta \in (0,2)$, 
$2^*=\frac{2N}{N-2}$ if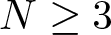 
$N \geq 3$ and 
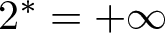$2^*=+\infty$ if N = 2. Related to the function 
$p:\mathbb{R}^{N}\rightarrow \mathbb{R}$, we assume that it is a continuous function with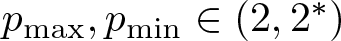 
$p_{\max}, p_{\min} \in (2,2^*)$, where 
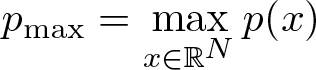$p_{\max}=\displaystyle \max_{x \in \mathbb{R}^N}p(x)$ and 
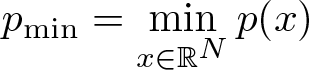$p_{\min}=\displaystyle \min_{x \in \mathbb{R}^N}p(x)$.
We show that for each λ > 0 the number of solutions is associated with the number of global maximum or global minimum points of p when ɛ is small enough. The proof of is based on the variational methods, Ekeland’s variational principle, Trundiger–Moser inequality, and the monotonicity of the ground state energy with respect to p. Our results extend those of Cao and Noussair (Multiplicity of positive and nodal solutions for nonlinear elliptic problem in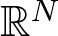 
$\mathbb{R}^{N}$. Ann. Inst. Henri Poincaré, Anal. Non Linéaire. 13 (1996), 567–588) and Ji, Wang and Wu (A monotone property of the ground state energy to the scalar field equation and applications. J. Lond. Math. Soc., II. Ser. 100 (2019), 804–824).
Keywords
MSC classification
Primary:
35A15: Variational methods
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2025. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh
References
Ait-Mahiout, K. and Alves, C.. Multiple solutions for a class of quasilinear problems in Orlicz-Sobolev spaces. Asymptotic Anal. 104 (2017), 49–66.CrossRefGoogle Scholar
Alves, C.. Existence and multiplicity of solution for a class of quasilinear. Adv. Nonlinear Stud. 5 (2005), 73–86.CrossRefGoogle Scholar
Alves, C. and de Freitas, L.. Multiplicity results for a class of quasilinear equations with exponential critical growth. Math. Nachr. 291 (2018), 222–244.CrossRefGoogle Scholar
Alves, C., do Ó, J. and Miyagaki, O.. On nonlinear perturbations of a periodic elliptic problem in 
$\mathbb{R}^2$ involving critical growth. Nonlinear Anal. Theory Methods Appl. Ser. A, Theory Methods. 56 (2004), 781–791.CrossRefGoogle Scholar
$\mathbb{R}^2$ involving critical growth. Nonlinear Anal. Theory Methods Appl. Ser. A, Theory Methods. 56 (2004), 781–791.CrossRefGoogle ScholarAlves, C. and Ferreira, M.. Existence of solutions for a class of p(x)-Laplacian equations involving a concave-convex nonlinearity with critical growth in
${\mathbb{R}}^N$. Topol. Methods Nonlinear Anal. 45 (2015), 399–422.CrossRefGoogle Scholar
${\mathbb{R}}^N$. Topol. Methods Nonlinear Anal. 45 (2015), 399–422.CrossRefGoogle ScholarAlves, C. and Figueiredo, G.. On multiplicity and concentration of positive solutions for a class of quasilinear problems with critical exponential growth in
$\mathbb{R}^{N}$. J. Differ. Equations 246 (2009), 1288–1311.CrossRefGoogle Scholar
$\mathbb{R}^{N}$. J. Differ. Equations 246 (2009), 1288–1311.CrossRefGoogle ScholarAlves, C. and Rădulescu, V.. The Lane-Emden equation with variable double-phase and multiple regime. Proc. Amer. Math. Soc. 148 (2020), 2937–2952.CrossRefGoogle Scholar
Alves, C. and Souto, M.. On existence and concentration behavior of ground state solutions for a class of problems with critical growth. Commun. Pure Appl. Anal. 1 (2002), 417–431.CrossRefGoogle Scholar
Berestycki, H. and Lions, P.. Nonlinear scalar field equations. I: Existence of a ground state. Arch. Ration. Mech. Anal. 82 (1983), 313–345.CrossRefGoogle Scholar
Bezerra do Ó, J.. Quasilinear elliptic equations with exponential nonlinearities. Commun. Appl. Nonlinear Anal. 2 (1995), 63–72.Google Scholar
Bezerra do Ó, J.. Semilinear Dirichlet problems for the N-Laplacian in
$\mathbb{R}^ N$ with nonlinearities in the critical growth range. Differ. Integral Equ. 9 (1996), 967–979.Google Scholar
$\mathbb{R}^ N$ with nonlinearities in the critical growth range. Differ. Integral Equ. 9 (1996), 967–979.Google ScholarBonder, J., Saintier, N. and Silva, A.. On the Sobolev embedding theorem for variable exponent spaces in the critical range. J. Differ. Equations 253 (2012), 1604–1620.CrossRefGoogle Scholar
Brézis, H. and Lieb, E.. A relation between pointwise convergence of functions and convergence of functionals. Proc. Am. Math. Soc. 88 (1983), 486–490.CrossRefGoogle Scholar
Brézis, H. and Nirenberg, L.. Positive solutions of nonlinear elliptic equations involving critical Sobolev exponents. Commun. Pure Appl. Math. 36 (1983), 437–477.CrossRefGoogle Scholar
Cao, D.. Existence of solutions for a class of p(x)-Laplacian equations involving a concave-convex nonlinearity with critical growth in
${\mathbb{R}}^N$. Commun. Partial Differ. Equations 17 (1992), .Google Scholar
${\mathbb{R}}^N$. Commun. Partial Differ. Equations 17 (1992), .Google ScholarCao, D. and Chabrowski, J.. Multiple solutions of nonhomogeneous elliptic equation with critical nonlinearity. Differ. Integral Equ. 10 (1997), 797–814.Google Scholar
Cao, D. and Noussair, E.. Multiplicity of positive and nodal solutions for nonlinear elliptic problem in
$\mathbb{R}^{N}$. Ann. Inst. Henri Poincaré, Anal. Non Linéaire. 13 (1996), 567–588.CrossRefGoogle Scholar
$\mathbb{R}^{N}$. Ann. Inst. Henri Poincaré, Anal. Non Linéaire. 13 (1996), 567–588.CrossRefGoogle ScholarCao, D. and Zhou, H.. Multiple positive solutions of nonhomogeneous semilinear elliptic equations in
$\mathbb{R}^{N} $. Proc. R. Soc. Edinb. Sect. A, Math. 126 (1996), 443–463.Google Scholar
$\mathbb{R}^{N} $. Proc. R. Soc. Edinb. Sect. A, Math. 126 (1996), 443–463.Google ScholarChambolle, A. and Lions, P.. Image recovery via total variation minimization and related problems. Numer. Math. 76 (1997), 167–188.CrossRefGoogle Scholar
Chen, Y., Levine, S. and Rao, M.. Variable exponent, linear growth functionals in image restoration. SIAM J. Appl. Math. 66 (2006), 1383–1406.CrossRefGoogle Scholar
de Figueiredo, D., Miyagaki, O. and Ruf, B.. Elliptic equations in
$\mathbb{R}^2$ with nonlinearities in the critical growth range. Calc. Var. Partial Differ. Equ. 3 (1995), 139–153.CrossRefGoogle Scholar
$\mathbb{R}^2$ with nonlinearities in the critical growth range. Calc. Var. Partial Differ. Equ. 3 (1995), 139–153.CrossRefGoogle Scholarde Figueiredo, D., Miyagaki, O. and Ruf, B.. On an inequality by N. Trudinger and J. Moser and related elliptic equations. Commun. Pure Appl. Math. 55 (2002), 135–152.CrossRefGoogle Scholar
Diening, L., Harjulehto, P., Hästö, P. and Růžička, M.. Lebesgue and Sobolev spaces with variable exponents (Springer, Berlin, 2011).CrossRefGoogle Scholar
do Ó, J., de Souza, M., de Medeiros, E. and Severo, U.. An improvement for the Trudinger-Moser inequality and applications. J. Differ. Equations 256 (2014), 1317–1349.CrossRefGoogle Scholar
Ekeland, I.. On the variational principle. J. Math. Anal. Appl. 47 (1974), 324–353.CrossRefGoogle Scholar
Fan, X.. p(x)-Laplacian equations in
$\mathbb{R}^N$ with periodic data and nonperiodic perturbations. J. Math. Anal. Appl. 341 (2008), 103–119.CrossRefGoogle Scholar
$\mathbb{R}^N$ with periodic data and nonperiodic perturbations. J. Math. Anal. Appl. 341 (2008), 103–119.CrossRefGoogle ScholarFan, X. and Zhao, D.. On the spaces
$L^{p(x)}(\Omega)$ and
$W^{m,p(x)}(\Omega)$. J. Math. Anal. Appl. 263 (2001), 424–446.CrossRefGoogle Scholar
$L^{p(x)}(\Omega)$ and 
$W^{m,p(x)}(\Omega)$. J. Math. Anal. Appl. 263 (2001), 424–446.CrossRefGoogle ScholarGarcia Azorero, J. and Peral Alonso, I.. Multiplicity of solutions for elliptic problems with critical exponent or with a nonsymmetric term. Trans. Am. Math. Soc. 323 (1991), 877–895.CrossRefGoogle Scholar
Gidas, B., Ni, W. and Nirenberg, L.. Symmetry of positive solutions of nonlinear elliptic equations in
$\mathbb{R}^N$. Adv. Math. Suppl. Stud. 7A (1981), 369–402.Google Scholar
$\mathbb{R}^N$. Adv. Math. Suppl. Stud. 7A (1981), 369–402.Google ScholarGilbarg, D. and Trudinger, N.. Elliptic partial differential equations of second order (Springer, Berlin, 2001).CrossRefGoogle Scholar
Hsu, T., Lin, H. and Hu, C.. Multiple positive solutions of quasilinear elliptic equations in
$\mathbb{R}^{N}$. J. Math. Anal. Appl. 388 (2012), 500–512.CrossRefGoogle Scholar
$\mathbb{R}^{N}$. J. Math. Anal. Appl. 388 (2012), 500–512.CrossRefGoogle ScholarHu, K. and Tang, C.. Existence and multiplicity of positive solutions of semilinear elliptic equations in unbounded domains. J. Differ. Equations 251 (2011), 609–629.CrossRefGoogle Scholar
Ji, C., Wang, Z. and Wu, Y.. A monotone property of the ground state energy to the scalar field equation and applications. J. Lond. Math. Soc. II. Ser. 100 (2019), 804–824.CrossRefGoogle Scholar
Kavian, O.. Introduction à la théOrie des Points Critiques et Applications aux problèmes elliptiques, Math. Appl. (Berl.) (Springer-Verlag, Paris, 1993).Google Scholar
Kwong, M. K.. Uniqueness of positive solutions of
$\Delta u-u+u^ p=0$ in Rn. Arch. Ration. Mech. Anal. 105 (1989), 243–266.CrossRefGoogle Scholar
$\Delta u-u+u^ p=0$ in Rn. Arch. Ration. Mech. Anal. 105 (1989), 243–266.CrossRefGoogle ScholarLin, H.. Multiple positive solutions for semilinear elliptic systems. J.Math. Anal. Appl. 391 (2012), 107–118.CrossRefGoogle Scholar
Lions, P.. The concentration-compactness principle in the calculus of variations. The locally compact case. II. Ann. Inst. Henri Poincaré, Anal. Non Linéaire. 1 (1984), 223–283.CrossRefGoogle Scholar
Mihăilescu, M. and Rădulescu, V.. On a nonhomogeneous quasilinear eigenvalue problem in Sobolev spaces with variable exponent. Proc. Amer. Math. Soc. 135 (2007), 2929–2937.CrossRefGoogle Scholar
Miyagaki, O.. On a class of semilinear elliptic problems in
$\mathbb{R}^ N$ with critical growth. Nonlinear Anal. Theory Methods Appl. 29 (1997), 773–781.CrossRefGoogle Scholar
$\mathbb{R}^ N$ with critical growth. Nonlinear Anal. Theory Methods Appl. 29 (1997), 773–781.CrossRefGoogle ScholarRuf, B.. A sharp Trudinger-Moser type inequality for unbounded domains in
$\mathbb{R}^2$. J. Funct. Anal. 219 (2005), 340–367.CrossRefGoogle Scholar
$\mathbb{R}^2$. J. Funct. Anal. 219 (2005), 340–367.CrossRefGoogle ScholarRůžička, M.. Electrorheological fluids: modeling and mathematical theory, Lecture Notes in Mathematics, Vol. 1748 (Springer-Verlag, Berlin, 2000).Google Scholar
Struwe, M.. Variational methods. Applications to nonlinear partial differential equations and Hamiltonian systems. 4th edn (Springer, Berlin, 2008).Google Scholar
Tarantello, G.. On nonhomogeneous elliptic equations involving critical Sobolev exponent. Ann. Inst. Henri Poincaré, Anal. Non Linéaire. 9 (1992), 281–304.CrossRefGoogle Scholar
Wu, T.. Multiplicity of positive solutions for semilinear elliptic equations in
$\mathbb{R}^{N}$. Proc. Roy. Soc. Edinburgh Sect. A. 138 (2008), 647–670.CrossRefGoogle Scholar
$\mathbb{R}^{N}$. Proc. Roy. Soc. Edinburgh Sect. A. 138 (2008), 647–670.CrossRefGoogle ScholarWu, Y. and Wang, Z.. Global behavior of the ground state energy of the nonlinear scalar field equation (in Chinese). Sci. Sin. Math. 53 (2023), 25–40.Google Scholar