Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-27T12:00:14.814Z Has data issue: false hasContentIssue false
  • English
  • Français

Multiple solutions for a free boundary problem arising in plasma physics

Published online by Cambridge University Press:  03 October 2014

Zhongyuan Liu
Zhongyuan Liu*
Affiliation:
School of Mathematics and Information Science, Henan University, Kaifeng, Henan 475004, People's Republic of China, ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we study the existence of solutions for a free boundary problem arising in the study of the equilibrium of a plasma confined in a tokamak:

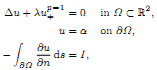
where p > 2, Ω is a bounded domain in ℝ2, n is the outward unit normal of ∂Ω, α is an unprescribed constant and I is a given positive constant. The set Ω+ = {x ∊ Ω: u(x) > 0} is called a plasma set. Under the condition that the homology of Ω is non-trivial, we show that for any given integer k ≥ 1 there exists λk > 0 such that for λ > λk the problem above has a solution with a plasma set consisting of k components.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 144 , Issue 5 , October 2014 , pp. 965 - 990
Copyright
Copyright © Royal Society of Edinburgh 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Ambrosetti, A. and Yang, J.. Asymptotic behaviour in planar vortex theory. Atti Accad. Naz. Lincei Rend. Cl. Sci. Fis. Mat. Natur. 78 (1990), 285–291.Google Scholar
2Bandle, C. and Marcus, M.. On the boundary values of solutions of a problem arising in plasma physics. Nonlin. Analysis 6 (1982), 1287–1294.CrossRefGoogle Scholar
3Bandle, C. and Sperb, R. P.. Qualitative behaviour and bounds in a nonlinear plasma problem. SIAM J. Math. Analysis 14 (1983), 142–151.CrossRefGoogle Scholar
4Berestycki, H. and Brézis, H.. Sur certains problemes de frontière libre. C. R. Acad. Sci. Paris I 283 (1976), 1091–1094.Google Scholar
5Berestycki, H. and Brézis, H.. On a free boundary value problem arising in plasma physics. Nonlin. Analysis 4 (1980), 415–436.CrossRefGoogle Scholar
6Caffarelli, L. and Friedman, A.. Asymptotic estimates for the plasma problem. Duke Math. J. 47 (1980), 705–742.CrossRefGoogle Scholar
7Cao, D., Peng, S. and Yan, S.. Multiplicity of solutions for the plasma problem in two dimensions. Adv. Math. 225 (2010), 2741–2785.CrossRefGoogle Scholar
8Cao, D., Liu, Z. and Wei, J.. Regularization of point vortices pairs for the Euler equation in dimension two. Arch. Ration. Mech. Analysis 212 (2014), 179–217.CrossRefGoogle Scholar
9Dancer, E. N. and Yan, S.. The Lazer-McKenna conjecture and a free boundary problem in two dimensions. J. Lond. Math. Soc. 78 (2008), 639–662.CrossRefGoogle Scholar
10Valeriola, S. De and Schaftingen, J. Van. Desingularization of vortex rings and shallow water vortices by semilinear elliptic problem. Arch. Ration. Mech. Analysis 210 (2013), 409–450.CrossRefGoogle Scholar
11Flucher, F. and Wei, J.. Asymptotic shape and location of small cores in elliptic free-boundary problems. Math. Z. 228 (1998), 638–703.CrossRefGoogle Scholar
12Fraenkel, L. E.. On steady vortex rings of small cross-section in an ideal fluid. Proc. R. Soc. Lond. A 316 (1970), 29–62.Google Scholar
13Fraenkel, L. E.. Examples of steady vortex rings of small cross-section in an ideal fluid. J. Fluid Mech. 51 (1972), 119–135.CrossRefGoogle Scholar
14Li, G., Yan, S. and Yang, J.. An elliptic problem related to planar vortex pairs. SIAM J. Math. Analysis 36 (2005), 1444–1460.CrossRefGoogle Scholar
15Li, Y. and Peng, S.. Multiple solutions for an elliptic problem related to vortex pairs. J. Diff. Eqns 250 (2011), 3448–3472.CrossRefGoogle Scholar
16Puel, J. P.. Sur un problème de valeur propre non linéaire et de frontière libre. C. R. Acad. Sci. Paris I 284 (1977), 861–863.Google Scholar
17Schaeffer, D.. Non-uniqueness in the equilibrium shape of a confined plasma. Commun. PDEs 2 (1977), 587–600.CrossRefGoogle Scholar
18Temam, R.. A nonlinear eigenvalue problem: the shape at equilibrium of a confined plasma. Arch. Ration. Mech. Analysis 60 (1975), 51–73.CrossRefGoogle Scholar
19Temam, R.. Remarks on a free boundary value problem arising in plasma physics. Commun. PDEs 2 (1977), 563–585.CrossRefGoogle Scholar
20Yang, J.. Existence and asymptotic behavior in planar vortex theory. Math. Models Meth. Appl. Sci. 1 (1991), 461–475.CrossRefGoogle Scholar
21Yang, J.. Global vortex rings and asymptotic behaviour. Nonlin. Analysis 25 (1995), 531–546.Google Scholar