Logarithmic upper bounds for weak solutions to a class of parabolic equations

Abstract

It is well known that a weak solution φ to the initial boundary value problem for the uniformly parabolic equation 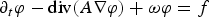$\partial _t\varphi - {\rm div}(A\nabla \varphi ) +\omega \varphi = f $ in 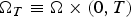$\Omega _T\equiv \Omega \times (0,T)$ satisfies the uniform estimate

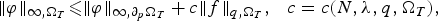$$\Vert \varphi \Vert_{\infty,\Omega_T}\les \Vert \varphi\Vert_{\infty,\partial_p\Omega_T}+c \Vert f \Vert_{q,\Omega_T}, \ \ \ c=c(N,\lambda, q, \Omega_T), $$

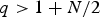provided that $q \gt 1+{N}/{2}$, where Ω is a bounded domain in 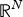${\open R}^N$ with Lipschitz boundary, T > 0, 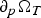$\partial _p\Omega _T$ is the parabolic boundary of 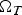$\Omega _T$, 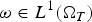$\omega \in L^1(\Omega _T)$ with 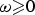$\omega \ges 0$, and λ is the smallest eigenvalue of the coefficient matrix A. This estimate is sharp in the sense that it generally fails if 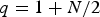$q=1+{N}/{2}$. In this paper, we show that the linear growth of the upper bound in 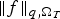$\Vert f \Vert_{q,\Omega _T}$ can be improved. To be precise, we establish

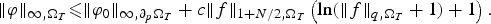$$ \Vert \varphi \Vert_{\infty,\Omega_T}\les \Vert \varphi_0 \Vert_{\infty,\partial_p\Omega_T}+c \Vert f \Vert_{1+{N}/{2},\Omega_T} \left(\ln(\Vert f \Vert_{q,\Omega_T}+1)+1\right). $$