No CrossRef data available.
Article contents
Locations of interior transition layers to inhomogeneous transition problems in higher -dimensional domains
Published online by Cambridge University Press: 08 March 2022
Abstract
We consider the following inhomogeneous problems
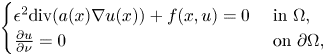
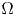 is a smooth and bounded domain in general dimensional space $\mathbb {R}^{N}$
is a smooth and bounded domain in general dimensional space $\mathbb {R}^{N}$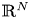 , $\epsilon >0$
, $\epsilon >0$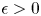 is a small parameter and function $a$
is a small parameter and function $a$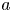 is positive. We respectively obtain the locations of interior transition layers of the solutions of the above transition problems that are $L^{1}$
is positive. We respectively obtain the locations of interior transition layers of the solutions of the above transition problems that are $L^{1}$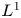 -local minimizer and global minimizer of the associated energy functional.
-local minimizer and global minimizer of the associated energy functional.
Keywords
MSC classification
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 153 , Issue 3 , June 2023 , pp. 764 - 783
- Copyright
- Copyright © The Author(s), 2022. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh



