Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-27T09:45:02.011Z Has data issue: false hasContentIssue false
  • English
  • Français

Liouville theorem for fractional Hénon–Lane–Emden systems on a half space

Part of: Elliptic equations and systems Miscellaneous topics - Partial differential equations Partial differential equations

Published online by Cambridge University Press:  17 September 2019

Phuong Le
Phuong Le*
Affiliation:
Division of Computational Mathematics and Engineering, Institute for Computational Science, Ton Duc Thang University, Ho Chi Minh City, Vietnam and Faculty of Mathematics and Statistics, Ton Duc Thang University, Ho Chi Minh City, Vietnam ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper is concerned with the fractional system

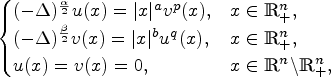\begin{cases} (-\Delta)^{\frac{\alpha}{2}} u(x) = \vert x \vert ^a v^p(x), &x\in\mathbb{R}^n_+,\\ (-\Delta)^{\frac{\beta}{2}} v(x) = \vert x \vert ^b u^q(x), &x\in\mathbb{R}^n_+,\\ u(x)=v(x)=0, &x\in\mathbb{R}^n{\setminus}\mathbb{R}^n_+, \end{cases}
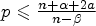where n ⩾ 2, 0 < α, β < 2, a > −α, b > −β and p, q ⩾ 1. By exploiting a direct method of scaling spheres for fractional systems, we prove that if $p \leqslant \frac {n+\alpha +2a}{n-\beta }$, 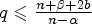$q \leqslant \frac {n+\beta +2b}{n-\alpha }$, 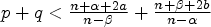$p+q<\frac {n+\alpha +2a}{n-\beta }+\frac {n+\beta +2b}{n-\alpha }$ and (u, v) is a nonnegative strong solution of the system, then u ≡ v ≡ 0.

Keywords

Fractional LaplacianHénon–Lane–Emden systemsLiouville theoremsmethod of scaling sphereshalf spaces

MSC classification

Primary: 35R11: Fractional partial differential equations
Secondary: 35J47: Second-order elliptic systems 35B53: Liouville theorems, Phragmén-Lindelöf theorems 35B09: Positive solutions
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 150 , Issue 6 , December 2020 , pp. 3060 - 3073
Check for updates
Copyright
Copyright © 2019 The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Caffarelli, L. and Silvestre, L.. An extension problem related to the fractional Laplacian. Comm. Partial Differential Equations 32 (2007), 1245–1260.Google Scholar
2Chen, W., Li, C., Zhang, L. and Cheng, T.. A Liouville theorem for α-harmonic functions in $\mathbb R_+^n$. Disc. Contin. Dyn. Syst. - A 36 (2015), 1721–1736.Google Scholar
3Chen, W., Fang, Y. and Yang, R.. Liouville theorems involving the fractional Laplacian on a half space. Adv. Math. 274 (2015), 167–198.CrossRefGoogle Scholar
4Chen, W., Li, C. and Li, Y.. A direct method of moving planes for the fractional Laplacian. Adv. Math. 308 (2017), 404–437.Google Scholar
5Chen, W., Li, Y. and Zhang, R.. A direct method of moving spheres on fractional order equations. J. Funct. Anal. 272 (2017), 4131–4157.Google Scholar
6Dai, W. and Qin, G.. Liouville type theorems for fractional and higher order Hénon-Hardy equations via the method of scaling spheres. arXiv:1810.02752 (2018).Google Scholar
7Duong, A. T. and Le, P.. Symmetry and nonexistence results for a fractional Hénon-Hardy system on a half space. Rocky Mountain J. Math. 49 (2019), 789–816.CrossRefGoogle Scholar
8Fall, M. and Weth, T.. Nonexistence results for a class of fractional elliptic boundary values problems. J. Funct. Anal. 263 (2012), 2205–2227.CrossRefGoogle Scholar
9Kulczycki, T.. Properties of Green function of symmetric stable processes. Probab. Math. Statist. 17 (1997), 339–364.Google Scholar
10Li, Y. Y. and Zhu, M.. Uniqueness theorems through the method of moving spheres. Duke Math. J. 80 (1995), 383–417.Google Scholar
11Quaas, A. and Xia, A.. Liouville type theorems for nonlinear elliptic equations and systems involving fractional Laplacian in the half space. Calc. Var. Partial Differential Equations 52 (2015), 641–659.Google Scholar
12Reichel, W. and Weth, T.. A priori bounds and a Liouville theorem on a half space for higher-order elliptic Dirichlet problems. Math. Z. 261 (2009), 805–827.CrossRefGoogle Scholar
13Tang, S. and Dou, J.. Nonexistence results for a fractional Hénon-Lane-Emden equation on a half space. Internat. J. Math. 26 (2015), 1550110.CrossRefGoogle Scholar
14Zhang, L. and Wang, Y.. Symmetry of solutions to semilinear equations involving the fractional Laplacian on $\mathbb R^n$ and $\mathbb R_+^n$. https://arxiv.org/abs/1610.00122 (2016).Google Scholar
15Zhang, L., Yu, M. and He, J.. A Liouville theorem for a class of fractional systems in $\mathbb R_+^n$. J. Differential Equations 263 (2017), 6025–6065.CrossRefGoogle Scholar