Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-12-04T19:22:43.892Z Has data issue: false hasContentIssue false
  • English
  • Français

Jacobi's elliptic functions and Lagrangian immersions

Published online by Cambridge University Press:  14 November 2011

Bang-Yen Chen
Bang-Yen Chen
Affiliation:
Department of Mathematics, Michigan State University, East Lansing, Michigan 48824-1027, U.S.A. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

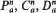First, we establish a sharp inequality between the squared mean curvature and the scalar curvature for a Lagrangian submanifold in a nonflat complex-space-form. Then, by utilising the Jacobi's elliptic functions en and dn, we introduce three families of Lagrangian submanifolds and two exceptional Lagrangian submanifolds Fn, Ln in nonflat complex-space-forms which satisfy the equality case of the inequality. Finally, we obtain the complete classification of Lagrangian submanifolds in nonflat complex-space-forms which satisfy this basic equality.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 126 , Issue 4 , 1996 , pp. 687 - 704
Copyright
Copyright © Royal Society of Edinburgh 1996

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Bowman, F.. Introduction to Elliptic Functions with Applications (New York: John Wiley, 1961).Google Scholar
2Byrd, P. F. and Friedman, M. D.. Handbook of Elliptic Integrals for Engineers and Scientists (Berlin: Springer, 1971).CrossRefGoogle Scholar
3Chen, B. Y.. Geometry of Submanifolds (New York: M. Dekker, 1973).Google Scholar
4Chen, B. Y., Dillen, F., Verstraelen, L. and Vrancken, L.. Totally real submanifolds of ℂPn satisfying a basic equality. Arch. Math. (Basel) 63 (1994), 553–64.CrossRefGoogle Scholar
5Chen, B. Y., Dillen, F., Verstraelen, L. and Vrancken, L.. An exotic totally real minimal immersion of S 3 in ℂP 3 and its characterisation. Proc. Roy. Soc. Edinburgh Sect. A 126 (1996), 153–65.CrossRefGoogle Scholar
6Chen, B. Y., Ludden, G. D. and Montiel, S.. Real submanifolds of a Kaehler manifold. Algebra Groups Geom. 1(1984), 176–212.Google Scholar
7Chen, B.-Y. and Oguie, K.. On totally real submanifolds. Trans. Amer. Math. Soc. 193 (1974), 257–66.CrossRefGoogle Scholar
8Dillen, F. and Nolker, S.. Semi-parallelity, multi-rotation surfaces and the helix-property. J. Reine Angew. Math. 435 (1993), 33–63.Google Scholar
9Hiepko, S.. Eine innere Kennzeichung der verzerrten Produkte. Math. Ann. 241 (1979), 209–15.CrossRefGoogle Scholar
10Nölker, S.. Isometric immersions of warped products. Differential Geom. Appl. (to appear).Google Scholar
11O'Neill, B.. Semi-Riemannian Geometry with Applications to Relativity (New York: Academic Press, 1983).Google Scholar
12Reckziegel, H.. Horizontal lifts of isometric immersions into the bundle space of a pseudo-Riemannian submersion. Global Differential Geometry and Global Analysis (1984), Lecture Notes in Mathematics 1156, pp. 264–79 (Berlin: Springer, 1985).Google Scholar