Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T18:02:56.007Z Has data issue: false hasContentIssue false
  • English
  • Français

Isoperimetric bounds for higher eigenvalue ratios for the n-dimensional fixed membrane problem

Published online by Cambridge University Press:  14 November 2011

Mark S. Ashbaugh  and
Rafael D. Benguria
Mark S. Ashbaugh
Affiliation:
Department of Mathematics, University of Missouri, Columbia, MO 65211, U.S.A. e-mail: [email protected]
Rafael D. Benguria
Affiliation:
Facultad de Física, P. Universidad Católica de Chile, Avda. Vicuña Mackenna 4860, Casilla 306, Santiago 22, Chile e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Synopsis

We give several results which extend our recent proof of the Payne-Pólya–Weinberger conjecture to ratios of higher eigenvalues. In particular, we show that for a bounded domain Ω⊂ℝn the eigenvalues of its Dirichlet Laplacian obey 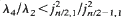where λm denotes the mth eigenvalue and jp,k denotes the kth positive zero of the Bessel function Jp(x). Certain extensions of this result are given, the most general being the bound 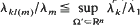where k≧2 and l(m) denotes the number of nodal domains of an mth eigenfunction. Our results imply certain further conjectures of Payne, Pólya, and Weinberger concerning λ3/λ2 and λ4/λ3. In addition, we find a resonably good bound on λ4/λ1. We also briefly discuss extensions to Schrödinger operators and other elliptic eigenvalue problems.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 123 , Issue 6 , 1993 , pp. 977 - 985
Copyright
Copyright © Royal Society of Edinburgh 1993

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Abramowitz, M. and Stegun, I. A. (eds). Handbook of Mathematical Functions, National Bureau of Standards Applied Mathematics Series 55 (Washington, D.C: U.S. Government Printing Office, 1964).Google Scholar
2Arnol'd, V. I., Vishik, M. I., Il'yashenko, Yu. S., Kalashnikov, A. S., Kondrat'ev, V. A., Kruzhkov, S. N., Landis, E. M., Millionshchikov, V. M., Oleinik, O. A., Filippov, A. F. and Shubin, M. A.. Some unsolved problems in the theory of differential equations and mathematical physics. Russian Math. Surveys 44:4 (1989), 157–171 (translation of Uspekhi Mat. Nauk 44:4 (1989), 191–202).Google Scholar
3Ashbaugh, M. S. and Benguria, R. D.. Optimal lower bounds for eigenvalue gaps for Schrödinger operators with symmetric single-well potentials and related results. In Maximum Principles and Eigenvalue Problems in Partial Differential Equations, ed. Schaefer, P. W., Pitman Research Notes in Mathematics 175, pp. 134–145 (Harlow: Longman, 1988).Google Scholar
4Ashbaugh, M. S. and Benguria, R. D.. Optimal bounds for ratios of eigenvalues of onedimensional Schrödinger operators with Dirichlet boundary conditions and positive potentials. Comm. Math. Phys. 124 (1989), 403–415.CrossRefGoogle Scholar
5Ashbaugh, M. S. and Benguria, R. D.. Proof of the Payne-Pólya-Weinberger conjecture. Bull. Amer. Math. Soc. 25 (1991), 19–29.CrossRefGoogle Scholar
6Ashbaugh, M. S. and Benguria, R. D.. A sharp bound for the ratio of the first two eigenvalues of Dirichlet Laplacians and extensions. Ann. Math. 135 (1992), 601–628.Google Scholar
7Ashbaugh, M. S. and Benguria, R. D.. Isoperimetric bound for λ3/λ2 for the membrane problem. Duke Math. J. 63 (1991), 333–341.Google Scholar
8Bandle, C.. Isoperimetric Inequalities and Applications, Pitman Monographs and Studies in Mathematics 7 (Boston: Pitman, 1980).Google Scholar
9Chavel, I.. Eigenvalues in Riemannian Geometry (New York: Academic Press, 1984).Google Scholar
10Courant, R. and Hilbert, D.. Methods of Mathematical Physics, vol. I (New York: Wiley Interscience, 1953).Google Scholar
11Gentry, R. D. and Banks, D. O.. Bounds for functions of eigenvalues of vibrating systems. J. Math. Anal. Appl. 51 (1975), 100–128.Google Scholar
12Mahar, T. J. and Willner, B. E.. An extremal eigenvalue problem. Comm. Pure Appl. Math. 29 (1976), 517–529.Google Scholar
13Payne, L. E., Pólya, G. and Weinberger, H. F.. Sur le quotient de deux fréquences propres consécutives. C. R. Acad. Sci. Paris 241 (1955), 917–919.Google Scholar
14Payne, L. E., Pólya, G. and Weinberger, H. F.. On the ratio of consecutive eigenvalues. J. Math, and Phys. 35 (1956), 289–298.CrossRefGoogle Scholar
15Reed, M. and Simon, B., Methods of Modern Mathematical Physics, vol IV: Analysis of Operators (New York: Academic Press, 1978).Google Scholar
16Thompson, C. J., On the ratio of consecutive eigenvalues in n-dimensions. Stud. Appl. Math. 48 (1969), 281–283.Google Scholar