Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T17:07:29.291Z Has data issue: false hasContentIssue false
  • English
  • Français

Integral representation of functionals defined on curves of W1,p

Published online by Cambridge University Press:  14 November 2011

Micol Amar ,
Giovanni Bellettini  and
Sergio Venturini
Micol Amar
Affiliation:
Dipartimento di Matematica, Università di Pavia, Via Abbiategrasso 215, 27100 Pavia, Italy, E-mail: [email protected]
Giovanni Bellettini
Affiliation:
Dipartimento di Matematica Applicata, Università di Pisa, Via Bonanno 25, 56126 Pisa, Italy, E-mail: [email protected]
Sergio Venturini
Affiliation:
Dipartimento di Matematica, Università di Bologna, Piazza di Porta S. Donato 5, 40127 Bologna, Italy, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let I ⊂ ℝ be a bounded open interval, 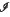(I) be the family of all open subintervals of I and let p > 1. The aim of this paper is to give an integral representation result for abstract functionals F: W1,p(I;ℝn) × 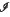(I) → [0, + ∞) which are lower semicontinuous and satisfy suitable properties. In particular, we prove an integral representation theorem for the Г-limit of a sequence {Fh}h, of functionals of the form

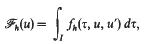
where each fh is a Borel function satisfying proper growth conditions.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 128 , Issue 2 , 1998 , pp. 193 - 217
Copyright
Copyright © Royal Society of Edinburgh 1998

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Alberti, G. and Buttazzo, G.. Integral representation of functionals denned on Sobolev spaces. In Composite Media and Homogenization Theory, Trieste, 1990, pp. 1–12 (Boston: Birkhäuser, 1991).Google Scholar
2Amar, M. and Bellettini, G.. A notion of total variation depending on a metric with discontinuous coefficients. Ann. Inst. H. Poincare, Anal. Non Lineaire 11 (1994), 91–133.CrossRefGoogle Scholar
3Ambrosio, L.. Relaxation of autonomous functionals with discontinuous integrands. Ann. Univ. Ferrara Sez. VII (N.S.) (1988), 21–47.CrossRefGoogle Scholar
4Ambrosio, L.. A lower closure theorem for autonomous orientor fields. Proc. Roy. Soc. Edinburgh Sect. A 110 (1988), 249–54.CrossRefGoogle Scholar
5Bouchitté, G. and Buttazzo, G.. Integral representation of nonconvex functionals defined on measures. Ann. Inst. H. Poincaré, Anal. Non Linéaire 9 (1992), 101–17.CrossRefGoogle Scholar
6Buttazzo, G.. Semicontinuity, Relaxation and Integral Representation Problems in the Calculus of Variations, Pitman Research Notes in Mathematics (Harlow: Longman, 1989).Google Scholar
7Buttazzo, G. and Maso, G. Dal. Integral representation and relaxation of local functionals. Nonlinear Anal. 9 (1985), 515–32.CrossRefGoogle Scholar
8Buttazzo, G. and Maso, G. Dal. A characterization of nonlinear functionals on Sobolev spaces which admit an integral representation with a Charatheodory integrand. J. Math. Pures Appl. 64 (1985), 337–61.Google Scholar
9Buttazzo, G. and Leaci, A.. Relaxation results for a class of variational integrals. J. Fund. Anal. 61 (1985), 360–77.CrossRefGoogle Scholar
10Dacorogna, B.. Weak Continuity and Weak Lower Semicontinuity of Nonlinear Functionals, Lecture Notes in Mathematics 922 (Berlin: Springer, 1982).CrossRefGoogle Scholar
11Dacorogna, B.. Direct Methods in the Calculus of Variations (Berlin: Springer, 1989).CrossRefGoogle Scholar
12Maso, G. Dal. An Introduction to I'-Convergence (Boston: Birkhäuser, 1993).Google Scholar
13Maso, G. Dal and Modica, L.. Integral functional determined by their minima. Rend. Sem. Mat. Univ. Padova 76 (1986), 255–67.Google Scholar
14De Cecco, G. and Palmieri, G.. Distanza intrinseca su una varieta finsleriana di Lipschitz. Rend. Accad. Naz. Sci. XL Mem. Mat. (5) 17 (1) (1993), 129–51.Google Scholar
15De Giorgi, E.. Teoremi di semicontinuitàa nel calcolo delle variazioni (Notes of a course held at the Istituto Nazionale di Alta Matematica, Roma, 1968–9).Google Scholar
16De Giorgi, E., Buttazzo, G. and Maso, G. Dal. On the lower semicontinuity of certain integral functionals. Atti Accad. Naz. Lincei Cl. Sci. Fis. Mat. Natur. Rend. Lincei (8) Mat. Appl. 74 (5) (1983), 274–82.Google Scholar
17De Giorgi, E. and Franzoni, T.. Su un tipo di convergenza variazionale. Atti Accad. Naz. Lincei Cl. Sci. Fis. Mat. Natur. Rend. Lincei (8) Mat. Appl. 58 (8) (1975), 842–50.Google Scholar
18Ekeland, I. and Temam, R.. Convex Analysis and Variational Problems (Amsterdam: North-Holland, 1978).Google Scholar
19Ioffe, A. D.. On lower semicontinuity of integral functionals I. II. SIAM J. Control Optim. 15 (1977), 521–38; 991–1000.CrossRefGoogle Scholar
20Kolmogorov, A. and Fomine, S.. Éléments de la Théorie des fonctions et de l'analyse fonctionelle (Moscow: Mir, 1977).Google Scholar
21Marcellini, P. and Sbordone, C.. Semicontinuity problems in the calculus of variations. Nonlinear Anal. 4 (1980), 241–57.CrossRefGoogle Scholar
22Marcus, M. and Mizel, V. J.. A characterization of non-linear functionals on W1,p possessing autonomous kernels. I. Pacific J. Math. 65 (1976), 135–58.CrossRefGoogle Scholar
23Rinow, W.. Die Innere Geometrie der Metrischen Raume (Berlin: Springer, 1961).CrossRefGoogle Scholar
24Serrin, J.. On the definition and properties of certain variational integrals. Trans. Amer. Math. Soc. 101 (1961), 139–67.CrossRefGoogle Scholar