Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T19:37:00.620Z Has data issue: false hasContentIssue false
  • English
  • Français

Infinite families of congruences modulo 5 and 7 for the cubic partition function

Part of: Combinatorics Additive number theory; partitions

Published online by Cambridge University Press:  16 January 2019

Olivia X. M. Yao
Olivia X. M. Yao*
Affiliation:
Department of Mathematics, Jiangsu University, Zhenjiang, Jiangsu 212013P. R. China ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

In 2010, Hei-Chi Chan introduced the cubic partition function a(n) in connection with Ramanujan's cubic continued fraction. Chen and Lin, and Ahmed, Baruah and Dastidar proved that a(25n + 22) ≡ 0 (mod 5) for n ⩾ 0. In this paper, we prove several infinite families of congruences modulo 5 and 7 for a(n). Our results generalize the congruence a(25n + 22) ≡ 0 (mod 5) and four congruences modulo 7 for a(n) due to Chen and Lin. Moreover, we present some non-standard congruences modulo 5 for a(n) by using an identity of Newman. For example, we prove that 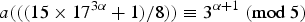$a((({15\times 17^{3\alpha }+1})/{8})) \equiv 3^{\alpha +1} \ ({\rm mod}\ 5)$ for α ⩾ 0.

Keywords

cubic partitionscongruencesθ function identities

MSC classification

Primary: 05A17: Partitions of integers
Secondary: 11P83: Partitions; congruences and congruential restrictions
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 149 , Issue 5 , October 2019 , pp. 1189 - 1205
Copyright
Copyright © Royal Society of Edinburgh 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Ahmed, Z., Baruah, N. D. and Dastidar, M. G.. New congruences modulo 5 for the number of 2-color partitions. J. Number Theory 157 (2015), 184–198.Google Scholar
2Andrews, G. E.. The theory of partitions (Reading: Addison-Wesley, 1976). reprinted, Cambridge University Press, Cambridge, 1984, 1998.Google Scholar
3Berndt, B. C.. Ramanujan's notebooks Part III (New York: Springer, 1991).Google Scholar
4Chan, H.-C.. Ramanujan's cubic continued fraction and a generalization of his “most beautiful identity”. Int. J. Number Theory 6 (2010), 673–680.Google Scholar
5Chan, H.-C.. Ramanujan's cubic continued fraction and Ramanujan type congruences for a certain partition function. Int. J. Number Theory 6 (2010), 819–834.Google Scholar
6Chen, W. Y. C. and Lin, B. L. S., Congruences for the number of cubic partitions derived from modular forms, preprint (arXiv: 0910.1263).Google Scholar
7Chern, S.. New congruences for 2-color partitions. J. Number Theory 163 (2016), 474–481.Google Scholar
8Hirschhorn, M. D.. Ramanujan's “most beautiful identity”. Am. Math. Monthly 118 (2011), 839–845.Google Scholar
9Lin, B. L. S., Arithmetric properties of certain partition functions, Ph.D. Thesis, Nankai University, 2011.Google Scholar
10Newman, M.. Modular forms whose coefficients possess multiplicative properties. Ann. Math. 70 (1959), 478–489.Google Scholar
11Ramanujan, S.. Collected Papers. In (eds.Hardy, G. H., Seshu Aiyar, P. V. and Wilson, B. M.) Some properties of p(n), the number of partitions of n. (Providence, RI: AMS Chelsea, 2000), pp. 210–213.Google Scholar