Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Howie, J. M.
1980.
Products of idempotents in finite full transformation semigroups.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 86,
Issue. 3-4,
p.
243.
Howie, J.M.
1980.
Semigroups.
p.
111.
Howie, J. M.
1981.
Some subsemigroups of infinite full transformation semigroups.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 88,
Issue. 1-2,
p.
159.
Gomes, Gracinda M. S.
and
Howie, John M.
1987.
On the ranks of certain finite semigroups of transformations.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 101,
Issue. 3,
p.
395.
Howie, John M.
1987.
Semigroups and Their Applications.
p.
57.
Brown, B.
and
Higgins, P. M.
1988.
Finite full transformation semigroups as collections of random functions.
Glasgow Mathematical Journal,
Vol. 30,
Issue. 2,
p.
203.
Higgins, Peter M.
1988.
Digraphs and the semigroup of all functions on a finite set.
Glasgow Mathematical Journal,
Vol. 30,
Issue. 1,
p.
41.
Umar, Abdullahi
1992.
On the semigroups of order-decreasing finite full transformations.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 120,
Issue. 1-2,
p.
129.
McAlister, Donald B.
1998.
Semigroups generated by a group and an idempotent.
Communications in Algebra,
Vol. 26,
Issue. 2,
p.
243.
Hirsch, Robin
and
Hodkinson, Ian
2001.
Relation algebras from cylindric algebras, I.
Annals of Pure and Applied Logic,
Vol. 112,
Issue. 2-3,
p.
225.
Yang, Xiuliang
2001.
MAXIMAL SUBSEMIGROUPS OF THE FINITE SINGULAR TRANSFORMATION SEMIGROUP.
Communications in Algebra,
Vol. 29,
Issue. 3,
p.
1175.
2002.
Relation Algebras by Games.
Vol. 147,
Issue. ,
p.
629.
Levi, Inessa
and
Seif, Steve
2003.
Constructive techniques for labeling constant weight Gray codes with applications to minimal generating sets of semigroups.
Journal of Algebra,
Vol. 266,
Issue. 1,
p.
189.
Barnes, George
and
Levi, Inessa
2003.
Ranks of Semigroups Generated by Order-Preserving Transformations with a Fixed Partition Type.
Communications in Algebra,
Vol. 31,
Issue. 4,
p.
1753.
Xiuliang, Yang
and
Haobo, Yang
2005.
ℋ
-Trivial Transformation Semibands and Digraphs
.
Communications in Algebra,
Vol. 33,
Issue. 5,
p.
1461.
Yang, Xiuliang
and
Yang, Haobo
2009.
ISOMORPHISMS OF TRANSFORMATION SEMIGROUPS ASSOCIATED WITH SIMPLE DIGRAPHS.
Asian-European Journal of Mathematics,
Vol. 02,
Issue. 04,
p.
727.
East, James
2010.
A presentation for the singular part of the full transformation semigroup.
Semigroup Forum,
Vol. 81,
Issue. 2,
p.
357.
EAST, JAMES
2011.
ON THE SINGULAR PART OF THE PARTITION MONOID.
International Journal of Algebra and Computation,
Vol. 21,
Issue. 01n02,
p.
147.
Ayık, Gonca
Ayık, Hayrullah
Bugay, Leyla
and
Kelekci, Osman
2013.
Generating sets of finite singular transformation semigroups.
Semigroup Forum,
Vol. 86,
Issue. 1,
p.
59.
East, James
2013.
Defining relations for idempotent generators in finite full transformation semigroups.
Semigroup Forum,
Vol. 86,
Issue. 3,
p.
451.
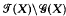 , the semigroup of all singular mappings of a finite set X into itself, is generated by its idempotents. Implicit in the method of proof, though not formally stated, is the result that if |X| = n then the n(n – 1) idempotents whose range has cardinal n – 1 form a generating set for. Here it is shown that if n ≧ 3 then a minimal set M of idempotent generators for
, the semigroup of all singular mappings of a finite set X into itself, is generated by its idempotents. Implicit in the method of proof, though not formally stated, is the result that if |X| = n then the n(n – 1) idempotents whose range has cardinal n – 1 form a generating set for. Here it is shown that if n ≧ 3 then a minimal set M of idempotent generators for 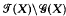 contains ½n(n–1) members. A formula is given for the number of distinct sets M.
contains ½n(n–1) members. A formula is given for the number of distinct sets M.

