Hostname: page-component-77c89778f8-7drxs Total loading time: 0 Render date: 2024-07-21T17:07:05.979Z Has data issue: false hasContentIssue false
  • English
  • Français

Hyers–Ulam stability for equations with differences and differential equations with time-dependent and periodic coefficients

Part of: Differential and difference algebra Stability theory

Published online by Cambridge University Press:  20 March 2019

Constantin Buşe ,
Vasile Lupulescu  and
Donal O'Regan
Constantin Buşe
Affiliation:
Politehnica University of Timişoara, Department of Mathematics, Timişoara, România ([email protected])
Vasile Lupulescu
Affiliation:
Constantin Brâncuşi University, Târgu Jiu, România ([email protected])
Donal O'Regan
Affiliation:
National University of Ireland, School of Mathematics, Statistics and Applied Mathematics, Galway, Ireland ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let q be a positive integer and let (an) and (bn) be two given ℂ-valued and q-periodic sequences. First we prove that the linear recurrence in ℂ 0.1

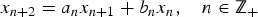$$x_{n + 2} = a_nx_{n + 1} + b_nx_n,\quad n\in {\open Z}_+ $$
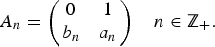is Hyers–Ulam stable if and only if the spectrum of the monodromy matrix Tq: = Aq−1 · · · A0 (i.e. the set of all its eigenvalues) does not intersect the unit circle Γ = {z ∈ ℂ: |z| = 1}, i.e. Tq is hyperbolic. Here (and in as follows) we let 0.2
$$A_n = \left( {\matrix{ 0 & 1 \cr {b_n} & {a_n} \cr } } \right)\quad n\in {\open Z}_+ .$$
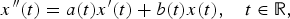Secondly we prove that the linear differential equation 0.3
$${x}^{\prime \prime}(t) = a(t){x}^{\prime}(t) + b(t)x(t),\quad t\in {\open R},$$
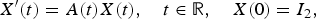 (where a(t) and b(t) are ℂ-valued continuous and 1-periodic functions defined on ℝ) is Hyers–Ulam stable if and only if P(1) is hyperbolic; here P(t) denotes the solution of the first-order matrix 2-dimensional differential system 0.4
$${X}^{\prime}(t) = A(t)X(t),\quad t\in {\open R},\quad X(0) = I_2,$$
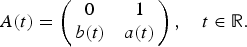where I2 is the identity matrix of order 2 and 0.5
$$A(t) = \left( {\matrix{ 0 & 1 \cr {b(t)} & {a(t)} \cr } } \right),\quad t\in {\open R}.$$

Keywords

Difference and differential equationsDiscrete dichotomyHyers–Ulam stability

MSC classification

Primary: 12H20: Abstract differential equations
Secondary: 34D09: Dichotomy, trichotomy 39B82: Stability, separation, extension, and related topics
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 150 , Issue 5 , October 2020 , pp. 2175 - 2188
Check for updates
Copyright
Copyright © Royal Society of Edinburgh 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Barbu, D., Buşe, C. and Tabassum, A.. Hyers-Ulam stability and discrete dichotomy. J. Math. Anal. Appl. 423 (2015), 1738–1752.CrossRefGoogle Scholar
2Barbu, D., Buşe, C. and Tabassum, A.. Hyers-Ulam stability and exponential dichotomy of linear differential periodic systems are equivalent. Electron J. Qual. Theory Differ. Equ. 58 (2015), 1–12.Google Scholar
3Brzdȩk, J. and Jung, S-M.. A note on stability of an operator linear equation of the second order. Abs. Appl. Anal. 2011 (2011), Article ID 602713, 15 pp.Google Scholar
4Brzdȩk, J., Piszczek, M.. On stability of the linear and polynomial functional equations in single variable. In Handbook of functional equations: stability theory (ed.Rassias, Th.M.), pp. 59–81 (New York/Heidelberg/Dordrecht/London: Springer Optimization and Its Applications, Springer, 2014).CrossRefGoogle Scholar
5Brzdȩk, J. and Wojcik, P.. On approximate solutions of some difference equations. Bull. Aust. Math. Soc. 95 (2017), 476–481.CrossRefGoogle Scholar
6Brzdȩk, J., Popa, D. and Xu, B.. Note on nonstability of the linear recurrence. Abh. Math. Sem. Uni. Hambburg 76 (2006), 183–189.CrossRefGoogle Scholar
7Brzdȩk, J., Popa, D. and Xu, B.. The Hyers-Ulam stability of nonlinear recurrences. J. Math. Anal. Appl. 335 (2007), 443–449.CrossRefGoogle Scholar
8Brzdȩk, J., Popa, D. and Xu, B.. Remarks on stability of linear recurrence of higher order. Appl. Math. Lett. 23 (2010), 1459–1463.CrossRefGoogle Scholar
9Brzdȩk, J., Popa, D., Raşa, I. and Xu, B.. Ulam stability of operators, mathematical analysis and its applications v. 1 (Oxford: Academic Press, Elsevier, 2018).Google Scholar
10Buşe, C., Saierli, O. and Tabassum, A.. Spectral characterizations for Hyers-Ulam stability. Electron. J. Qual. Theory. Differ. Equ. 30 (2014), 1–14.CrossRefGoogle Scholar
11Buşe, C., O'Regan, D., Saierli, O. and Tabassum, A.. Hyers-Ulam stability and discrete dichotomy for difference periodic systems. Bull. Sci. Math. 140 (2016), 908–934.CrossRefGoogle Scholar
12Cădariu, L. and Radu, V.. Fixed point methods for the generalized stability of functional equations in a single variable. Fixed Point Theory Appl. 2008 (2008), Article ID 749392.CrossRefGoogle Scholar
13Chu, H. Y., Ku, S. H., Park, J. S.. A note on envelops of homotopies. J. Diff. Equ. Appl. 21 (2015), 512–527.CrossRefGoogle Scholar
14Hamid, R., Soon-Mo, J. and Themistocles, M. R.. Laplace transform and Hyers-Ulam stability of linear differential equations. J. Math. Anal. Appl. 403 (2013), 244–251.Google Scholar
15Henry, D.. Geometric theory of semi-linear parabolic equations, Lecture Notes in Mathematics,vol. 840, iv+348 pp. (Berlin-New York: Springer Verlag, 1981).CrossRefGoogle Scholar
16Onitsuka, M. and Shoji, T.. Hyers-Ulam stability of first order homogeneous linear differential equations with a real valued coefficient. Appl. Math. Lett. 63 (2017), 102–108.CrossRefGoogle Scholar
17Perron, O.. Ueber eine Matrixtransformation. Math. Zeitschrift 22 (1930), 465–473.CrossRefGoogle Scholar
18Popa, D.. Hyers-Ulam stability of the linear recurrence with constant coefficients. Adv. Differ. Equ. 2005 (2005), 101–107.CrossRefGoogle Scholar
19Popa, D.. Hyers-Ulam-Rassias stability of a linear recurrence. J. Math. Anal. Appl. 369 (2005), 591–597.CrossRefGoogle Scholar
20Popa, D.. On the stability of the second order linear recurrence. Gazeta Matematică, Seria A XXX(CIX) (2012), 69–74.Google Scholar
21Popa, D. and Rasa, I.. On the Hyers-Ulam stability of the linear differential equations. J. Math. Anal. Appl. 381 (2011), 530–537.CrossRefGoogle Scholar
22Radu, V.. The fixed point alternative and the stability of functional equations. Fixed Point Theory 4 (2003), 91–96.Google Scholar
23Wang, J. R., Michal, F. and Ying, T.. Stability analysis for a general class of non-instantaneous impulsive differential equations. Mediteranean J. Math. 24 (2017).Google Scholar
24Xu, M.. Hyers-Ulam-Rassias stability of a system of first order linear recurrences. Bull. Korean Math. Soc. 44 (2007), 841–849.CrossRefGoogle Scholar
25Xu, B. and Brzdȩk, J.. Hyers-Ulam stability of a system of first order linear recurrences with constant coefficients. Discret. Dyn. Nat. Soc. 2015 (2015), Article ID 269356, 5 pp.CrossRefGoogle Scholar
26Xu, B., Brzdȩk, J. and Zhang, W.. Fixed point results and the Hyers-Ulam stability of linear equations of higher orders. Pacific J. Math. 273 (2015), 483–498.CrossRefGoogle Scholar
27Zada, A., Shah, S. O., Ismail, S. and Tongxing, L.. Hyers-Ulam stability in terms of dichotomy of first order linear dynamic systems. Panjab Univ. J. Math. 49 (2017), 37–47.Google Scholar
28Zhao, X.. Mean square Hyers-Ulam stability of stochastic differential equations driven by Brownian motion. Adv. Differ. Equ. 2016 (October 2016), Article 271.CrossRefGoogle Scholar