How do autodiffeomorphisms act on embeddings?

Abstract

We work in the smooth category. The following problem was suggested by E. Rees in 2002: describe the precomposition action of self-diffeomorphisms of S^p × S^q on the set of isotopy classes of embeddings S^p × S^q → ℝ^m.

Let G: S^p × S^q → ℝ^m be an embedding such that

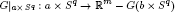
is null-homotopic for some pair of different points a, b ∈ S^p. We prove the following statement: if ψ is an autodiffeomorphism of S^p × S^q identical on a neighbourhood of a × S^q for some a ∈ S^p and p ⩽ q and 2m ⩾ 3p +3q + 4, then G◦ ψ is isotopic to G.

Let N be an oriented (p + q)-manifold and let f, g be isotopy classes of embeddings N → ℝ^m, S^p × S^q → ℝ^m, respectively. As a corollary we obtain that under certain conditions for orientation-preserving embeddings s: S^p × D^q → N the S^p-parametric embedded connected sum f#_sg depends only on f, g and the homology class of s|_{S^p × 0}.