No CrossRef data available.
Article contents
The homotopy decomposition of the suspension of a non-simply-connected five-manifold
Published online by Cambridge University Press: 17 April 2024
Abstract
In this paper we determine the homotopy types of the reduced suspension space of certain connected orientable closed smooth $five$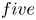 -manifolds. As applications, we compute the reduced $K$
-manifolds. As applications, we compute the reduced $K$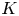 -groups of $M$
-groups of $M$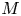 and show that the suspension map between the third cohomotopy set $\pi ^3(M)$
and show that the suspension map between the third cohomotopy set $\pi ^3(M)$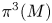 and the fourth cohomotopy set $\pi ^4(\Sigma M)$
and the fourth cohomotopy set $\pi ^4(\Sigma M)$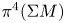 is a bijection.
is a bijection.
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright © The Author(s), 2024. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh
Footnotes
This article has been updated since original publication. A notice detailing this has been published.
References
An addendum has been issued for this article:
Linked content
Please note an has been issued for this article.



