Homogenization of the spectral problem on the Riemannian manifold consisting of two domains connected by many tubes

Abstract

The paper deals with the asymptotic behaviour as ε → 0 of the spectrum of the Laplace–Beltrami operator Δ^ε on the Riemannian manifold M^ε (dim M^ε = N ≥ 2) depending on a small parameter ε > 0. M^ε consists of two perforated domains, which are connected by an array of tubes of length q^ε. Each perforated domain is obtained by removing from the fixed domain Ω ⊂ ℝ^N the system of ε-periodically distributed balls of radius d^ε = ō(ε). We obtain a variety of homogenized spectral problems in Ω; their type depends on some relations between ε, d^ε and q^ε. In particular, if the limits

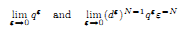
are positive, then the homogenized spectral problem contains the spectral parameter in a nonlinear manner, and its spectrum has a sequence of accumulation points.