Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-26T11:54:50.697Z Has data issue: false hasContentIssue false
  • English
  • Français

The homogenization of elliptic partial differential systems on rugous domains with variable boundary conditions

Published online by Cambridge University Press:  18 March 2013

J. Casado-Díaz ,
M. Luna-Laynez  and
F. J. Suárez-Grau
J. Casado-Díaz
Affiliation:
Departamento de Ecuaciones Diferenciales y Análisis Numérico, Facultad de Matemáticas, Universidad de Sevilla, C. Tarfía s/n, 41012 Sevilla, Spain ([email protected]; [email protected]; [email protected])
M. Luna-Laynez
Affiliation:
Departamento de Ecuaciones Diferenciales y Análisis Numérico, Facultad de Matemáticas, Universidad de Sevilla, C. Tarfía s/n, 41012 Sevilla, Spain ([email protected]; [email protected]; [email protected])
F. J. Suárez-Grau
Affiliation:
Departamento de Ecuaciones Diferenciales y Análisis Numérico, Facultad de Matemáticas, Universidad de Sevilla, C. Tarfía s/n, 41012 Sevilla, Spain ([email protected]; [email protected]; [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper is devoted to studying the asymptotic behaviour of a sequence of elliptic systems posed in a sequence of rough domains Ωn. The solutions un are assumed to satisfy un(x) ϵ Vn(x), where Vn(x) is a vectorial space depending on 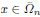. This enables one to consider several types of boundary conditions posed in variable sets of the boundary. For some choices of the vectorial spaces Vn(x), our study provides, in particular, some classical results for the homogenization of Dirichlet elliptic problems in varying domains.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 143 , Issue 2 , April 2013 , pp. 303 - 335
Copyright
Copyright © Royal Society of Edinburgh 2013

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)