Hostname: page-component-6bf8c574d5-rwnhh Total loading time: 0 Render date: 2025-02-22T19:27:43.391Z Has data issue: false hasContentIssue false
  • English
  • Français

Hilbert boundary value problems—a distributional approach

Published online by Cambridge University Press:  14 February 2012

Marion Orton
Marion Orton
Affiliation:
University of California, Irvine
Get access Rights & Permissions [Opens in a new window]

Synopsis

Hilbert boundary value problems for a half-space are considered for analytic representations of Schwartz distributions: given data g ∈D'(ℛ) and a coefficient x we seek functions F(z) analytic for Jmz≠0 whose limits 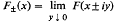exist in D'(ℛ) and satisfy F+—XF– = g on an open subset U of the real line R. U is the complement of a finite set which contains the singular support and the zeros of X·X and its reciprocal satisfy certain growth conditions near the boundary points of U. Solutions F(z) are shown to exist, and their general form is determined by obtaining a suitable factorisation of x.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 77 , Issue 3-4 , 1977 , pp. 193 - 208
Copyright
Copyright © Royal Society of Edinburgh 1977

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Bremermann, H.. Distributions, complex variables, and Fourier transforms of distributions (Redding, Mass.: Addison-Wesley, 1965).Google Scholar
2Carleman, T.. Über die Abelsche Integralgleichung mit konstanten Integrationsgrenzen. Math. Z. 15 (1922), 161–170.Google Scholar
3Čerskii, Ju.I.. Solutions of Riemann's boundary value problem in classes of generalized functions. Dokl. Akad. Nauk SSSR 125 (1959), 500–503.Google Scholar
4Gakhov, F. D.Boundary value problems (Oxford: Pergamon, 1966).CrossRefGoogle Scholar
5Gel'fand, I. M. and Shilov, G. E.. Generalized functions I, 11. (New York: Academic Press, 1964, 1968).Google Scholar
6Martineau, A.. Distributions et valeurs au bord des fonctions holomorphes. Proc. Int. Summer Conf. 196–326 (Lisbon: Inst. Gulbenkian Ci).Google Scholar
7Mitrović, D.. On a decomposition of distributions. Math. Balkanica 2 (1972), 156–160.Google Scholar
8Mitrović, D.. Some distributional boundary value problems. Math. Balkanica 2 (1972), 161–164.Google Scholar
9Muskhelishvili, N. J.. Singular integral equations (Groningen: Noordhoff, 1958).Google Scholar
10Orton, M.. Hilbert transforms, Plemelj relations, and Fourier transforms of distributions. SIAM J. Math. Anal. 4 (1973), 656–670.CrossRefGoogle Scholar
11Rogožin, V. S.. Riemann and Hilbert boundary value problems in the class of generalized functions. Sibirsk Mat. Ž. 2 (1961), 734–745.Google Scholar
12Rogožin, V. S.. A general scheme of solution of boundary value problems in the space of generalized functions. Dokl. Akad. Nauk SSSR 164 (1965), 277–280.Google Scholar
13Rogožin, V. S.. On the theory of the problem of Riemann in the class L p. Dokl. Akad. Nauk SSSR 180 (1968), 538–541.Google Scholar
14Srivastav, R. P.. Dual integral equations with trigonometric kernels and tempered distributions. SIAM J. Math. Anal. 3 (1972), 413–421.CrossRefGoogle Scholar
15Tillmann, H. G.. Darstellung der Schwartzschen Distributionen durch analytische Funktionen. Math. Z. 77 (1961), 106–124.CrossRefGoogle Scholar
16Tricomi, F. G.. Integral equations (New York: Interscience, 1957).Google Scholar