Article contents
The group of homotopy self-equivalences of non-simply-connected spaces using Postnikov decompositions II1
Published online by Cambridge University Press: 14 November 2011
Synopsis
We give here an abelian kernel (central) group extension sequence for calculating, for a non-simply-connected space X, the group of pointed self-homotopy-equivalence classes 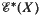 . This group extension sequence gives
. This group extension sequence gives 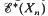 in terms of
in terms of 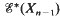 , where Xn is the nth stage of a Postnikov decomposition, and, in particular, determines
, where Xn is the nth stage of a Postnikov decomposition, and, in particular, determines 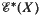 up to extension for non-simplyconnected spaces X having at most two non-trivial homotopy groups in dimensions 1 and n. We give a simple geometric proof that the sequence splits in the case where
up to extension for non-simplyconnected spaces X having at most two non-trivial homotopy groups in dimensions 1 and n. We give a simple geometric proof that the sequence splits in the case where 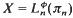 is the generalised Eilenberg–McLane space corresponding to the action ϕ: π1 → aut πn, and give some information about the class of the extension in the general case.
is the generalised Eilenberg–McLane space corresponding to the action ϕ: π1 → aut πn, and give some information about the class of the extension in the general case.
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 122 , Issue 1-2 , 1992 , pp. 127 - 135
- Copyright
- Copyright © Royal Society of Edinburgh 1992
References
- 2
- Cited by


