Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
do Ó, João Marcos
Giacomoni, Jacques
and
Mishra, Pawan Kumar
2019.
Nonautonomous fractional Hamiltonian system with critical exponential growth.
Nonlinear Differential Equations and Applications NoDEA,
Vol. 26,
Issue. 4,
Maia, B. B. V.
and
Miyagaki, O. H.
2022.
Existence and nonexistence results for a class of Hamiltonian Choquard-type elliptic systems with lower critical growth on ℝ2.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 152,
Issue. 6,
p.
1383.
Costa, Augusto C. R.
Maia, Bráulio B. V.
and
Miyagaki, Olímpio H.
2022.
On existence and concentration of solutions for Hamiltonian systems involving fractional operator with critical exponential growth.
Mathematische Nachrichten,
Vol. 295,
Issue. 8,
p.
1480.
Deng, Shengbing
and
Yu, Junwei
2022.
On a class of singular Hamiltonian Choquard-type elliptic systems with critical exponential growth.
Journal of Mathematical Physics,
Vol. 63,
Issue. 12,
Stapenhorst, Matheus F.
2022.
A singular problem with nonlinearities of exponential growth.
Nonlinear Differential Equations and Applications NoDEA,
Vol. 29,
Issue. 2,
Qin, Dongdong
Tang, Xianhua
and
Zhang, Jian
2022.
Ground states for planar Hamiltonian elliptic systems with critical exponential growth.
Journal of Differential Equations,
Vol. 308,
Issue. ,
p.
130.
Anthal, Gurdev C.
Giacomoni, Jacques
and
Sreenadh, Konijeti
2023.
A Choquard‐type equation with a singular absorption nonlinearity in two dimensions.
Mathematical Methods in the Applied Sciences,
Vol. 46,
Issue. 4,
p.
4510.
Guan, Minlan
Lai, Lizhen
Liu, Boxue
and
Qin, Dongdong
2024.
Ground state solutions for the Hamilton–Choquard elliptic system with critical exponential growth.
Asymptotic Analysis,
Vol. 140,
Issue. 3-4,
p.
159.
Severo, Uberlandio B.
Souza, Manassés de
and
Menezes, Marta
2024.
Hamiltonian systems involving exponential growth in $${\mathbb {R}}^{2}$$ with general nonlinearities.
Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas,
Vol. 118,
Issue. 1,
Chen, Peng
Wang, Zhengping
and
Wu, Yan
2024.
Ground State Solution for Strongly Indefinite X-Ray Free Electron Laser Schrödinger Equation.
The Journal of Geometric Analysis,
Vol. 34,
Issue. 12,
Anthal, G. C.
Do Ó, J. M.
Giacomoni, J.
and
Sreenadh, K.
2024.
Fractional Hamiltonian type system on $$\mathbb R$$ with critical growth nonlinearity.
Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas,
Vol. 118,
Issue. 1,
Deng, Shengbing
and
Yu, Junwei
2024.
Existence of solution for a class of fractional Hamiltonian-type elliptic systems with exponential critical growth in R.
Journal of Mathematical Physics,
Vol. 65,
Issue. 3,
Leuyacc, Yony Raúl Santaria
2024.
Singular Hamiltonian elliptic systems involving double exponential growth in dimension two.
Partial Differential Equations in Applied Mathematics,
Vol. 10,
Issue. ,
p.
100681.
Chen, Peng
Gu, Longjiang
and
Wu, Yan
2025.
Multiple solutions for a Hamiltonian elliptic system with sign-changing perturbation.
Acta Mathematica Scientia,
Vol. 45,
Issue. 2,
p.
602.
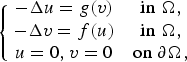 $$\left\{ {\matrix{ {-\Delta u = g(v)} & {{\rm in}\;\Omega,} \cr {-\Delta v = f(u)} & {{\rm in}\;\Omega,} \cr {u = 0,v = 0} & {{\rm on}\;\partial \Omega,} \cr } } \right.$$
$$\left\{ {\matrix{ {-\Delta u = g(v)} & {{\rm in}\;\Omega,} \cr {-\Delta v = f(u)} & {{\rm in}\;\Omega,} \cr {u = 0,v = 0} & {{\rm on}\;\partial \Omega,} \cr } } \right.$$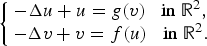 $$\left\{ {\matrix{ {-\Delta u + u = g(v)\;\;\;{\rm in}\;{\open R}^2,} \cr {-\Delta v + v = f(u)\;\;\;{\rm in}\;{\open R}^2.} \cr } } \right.$$
$$\left\{ {\matrix{ {-\Delta u + u = g(v)\;\;\;{\rm in}\;{\open R}^2,} \cr {-\Delta v + v = f(u)\;\;\;{\rm in}\;{\open R}^2.} \cr } } \right.$$


