Published online by Cambridge University Press: 30 January 2019
In this paper, we obtain gradient estimates of the positive solutions to weighted p-Laplacian type equations with a gradient-dependent nonlinearity of the form
0.1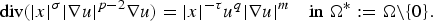 $${\rm div }( \vert x \vert ^\sigma \vert \nabla u \vert ^{p-2}\nabla u) = \vert x \vert ^{-\tau }u^q \vert \nabla u \vert ^m\quad {\rm in}\;\Omega^*: = \Omega {\rm \setminus }\{ 0\} .$$
$${\rm div }( \vert x \vert ^\sigma \vert \nabla u \vert ^{p-2}\nabla u) = \vert x \vert ^{-\tau }u^q \vert \nabla u \vert ^m\quad {\rm in}\;\Omega^*: = \Omega {\rm \setminus }\{ 0\} .$$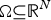 $\Omega \subseteq {\open R}^N$ denotes a domain containing the origin with
$\Omega \subseteq {\open R}^N$ denotes a domain containing the origin with 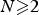 $N\ges 2$, whereas
$N\ges 2$, whereas 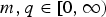 $m,q\in [0,\infty )$,
$m,q\in [0,\infty )$, 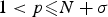 $1<p\les N+\sigma $ and
$1<p\les N+\sigma $ and 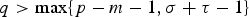 $q>\max \{p-m-1,\sigma +\tau -1\}$. The main difficulty arises from the dependence of the right-hand side of (0.1) on x, u and
$q>\max \{p-m-1,\sigma +\tau -1\}$. The main difficulty arises from the dependence of the right-hand side of (0.1) on x, u and 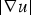 $ \vert \nabla u \vert $, without any upper bound restriction on the power m of
$ \vert \nabla u \vert $, without any upper bound restriction on the power m of 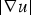 $ \vert \nabla u \vert $. Our proof of the gradient estimates is based on a two-step process relying on a modified version of the Bernstein's method. As a by-product, we extend the range of applicability of the Liouville-type results known for (0.1).
$ \vert \nabla u \vert $. Our proof of the gradient estimates is based on a two-step process relying on a modified version of the Bernstein's method. As a by-product, we extend the range of applicability of the Liouville-type results known for (0.1).