Global existence for the heat equation with nonlinear dynamical boundary conditions

Abstract

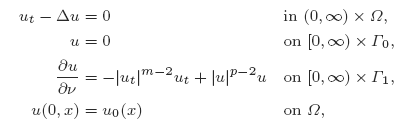This paper deals with local and global existence for the solutions of the heat equation in bounded domains with nonlinear boundary damping and source terms. The typical problem studied is where Ω ⊂ Rⁿ (n ≥ 1) is a regular and bounded domain, ∂Ω = Γ₀ ∪ Γ₁, m > 1, 2 ≤ p < r, where r = 2(n − 1)/(n − 2) when n ≥ 3, r = ∞ when n = 1, 2 and u₀ ∈ H¹(Ω), u₀ = 0 on Γ₀. We prove local existence of the solutions in H¹(Ω) when m > r/(r + 1−p) or n = 1, 2 and global existence when p ≤ m or the initial datum is inside the potential well associated to the stationary problem.